Алгебра и начала анализа для учащихся 11 класса поурочные планы
рассмотреть решение логарифмических неравенств и вырабатывать навыки их решения; проверить умение решать логарифмические уравнения - РЕШЕНИЕ ЛОГАРИФМИЧЕСКИХ УРАВНЕНИЙ И НЕРАВЕНСТВ - ПОКАЗАТЕЛЬНАЯ И ЛОГАРИФМИЧЕСКАЯ ФУНКЦИИ - 2-е полугодие
Цели: рассмотреть решение логарифмических неравенств и вырабатывать навыки их решения; проверить умение решать логарифмические уравнения.
Ход урока
I. Проверочная работа (15-20 мин)
Вариант I
1. Решить уравнения
а) № 519 (a), № 520 (б);
б) № 522 (a), № 523 (b).
2. Решить систему уравнений 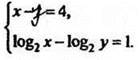
Вариант II
1. Решить уравнения
а) № 519 (б), № 520 (a);
б) № 522 (г), № 523 (г).
2. Решить систему уравнений 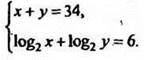
II. Изучение нового материала
1. Неравенство, содержащее переменную только под знаком логарифма, называется логарифмическим. .
2. Решение логарифмических неравенств основано на том, что функция у = logа х при а > 1 является монотонно возрастающей, а при 0 < а < 1 монотонно убывающей:
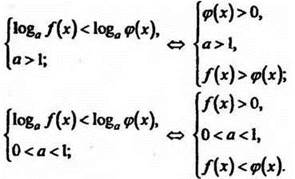
3. Логарифмическое неравенство вида ![]() эквивалентно двум системам неравенств:
эквивалентно двум системам неравенств:
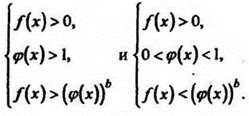
Аналогично решаются и логарифмические неравенства вида ![]()
4. По учебнику на стр. 233-234 разобрать решение примера 4.
5. Найти наибольшее целое х, удовлетворяющее неравенству:
![]()
Решение
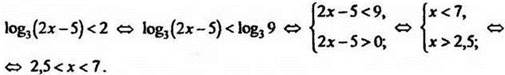
Наибольшее целое х = 6. Ответ: х = 6;
![]()
Решение
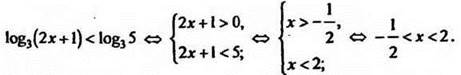
Наибольшее целое число х = 1. Ответ: х = 1;
![]()
Указание.
Преобразуем ![]()
Ответ: -1;
г) найти наибольшее целое х, удовлетворяющее неравенству ![]()
Решение
Логарифмическое неравенство эквивалентно совокупности двух систем неравенств
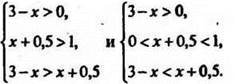
Решаем первую из этих систем:
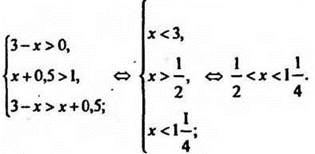
Решаем вторую систему:
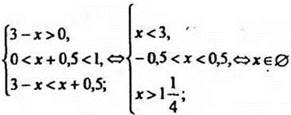
Решением исходного неравенства является объединение двух решений этих систем, т. е. 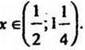 Наибольшее целое х из этого промежутка х = 1.
Наибольшее целое х из этого промежутка х = 1.
Ответ: 1.
6. Решить № 525 (а, б), № 526 (в, г).
III. Итоги урока
IV. Домашнее задание: п. 39; решить № 516, № 517, № 518, № 525 (в; г), № 526 (а; б).