Алгебра и начала анализа для учащихся 11 класса поурочные планы
Тригонометрические функции числового аргумента - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие
УРОК № 1
Тема. Тригонометрические функции числового аргумента
Цели: повторить основные формулы тригонометрии и закрепить их знание в ходе выполнения упражнений.
Ход урока
I. Анализ контрольной работы
II. Выполнение упражнений
1. Синус, косинус, тангенс и котангенс (повторение).
2. Основные формулы тригонометрии (повторение).
3. Упростите выражение ![]() и найдите его значение при
и найдите его значение при ![]() =
= ![]() /3. Ответ: cos
/3. Ответ: cos![]() ; 1/2.
; 1/2.
4. Докажите тождество  Укажите множество, на котором данное равенство не является тождеством.
Укажите множество, на котором данное равенство не является тождеством.
Указание.
Данное равенство не является тождеством на множестве, на котором ![]()
cos а = 0 или 1 + sin a = 0, ![]()
Множество чисел ![]() является подмножеством первого множества.
является подмножеством первого множества.
Ответ: данное равенство не является тождеством на множестве чисел ![]()
5. Самостоятельно решить
а) упростите выражение ![]()
Укажите множество значений х, при которых данное выражение не имеет смысла. Ответ: sin x; при ![]()
б) упростите выражение и вычислите его значение при а = -15°:
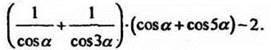
Ответ: 2cos 4a; 1.
6. Упростите выражение ![]()
Решени.
Используя формулу ![]() можно доказать, что
можно доказать, что

7. Объясняет учитель: рассмотрим задание: «От угла в 28° доберись до угла в 74,5°». Рассуждения проводим так:
28° ![]() дополнительный 62°
дополнительный 62° ![]() половинный 31°
половинный 31° ![]() половинный 15,5°
половинный 15,5° ![]() дополнительный 74,5°.
дополнительный 74,5°.
Еще пример: 10° ![]() 80°
80° ![]() 40°
40° ![]() 50°
50° ![]() 25°
25° ![]() 65°
65° ![]() 32,5°.
32,5°.
Таким образом, от угла в 10° мы добрались до угла в 32°30.
Воспользуемся этими рассуждениями при доказательстве тождества ![]()
Рассуждаем так: ![]() Тогд.
Тогд.

8. Сократить дробь: ![]()
Подготовка к решению: 24° ![]() 66°
66° ![]() 33° или 33°
33° или 33° ![]() 66°
66° ![]() 24°.
24°.
Два решения:
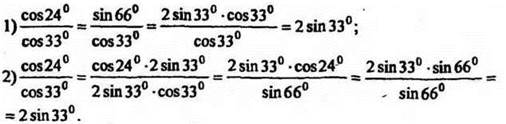
9. Упростите выражение:
![]()

10. Доказать тождества (самостоятельно):

11*. Найти sin6 а, + cos6 а, если sin a cos а = m.
Решение
Находим ![]()
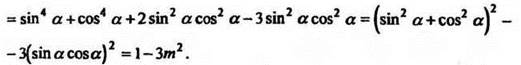
12. Самостоятельно решить: известно, что sin а + cos а = m.
Найти: ![]()
Ответ: 
III. Итоги урока
IV. Домашнее задание: повторить § 3 - тему «Решение тригонометрических уравнений и неравенств»; решить на стр. 271 № 54, № 56, № 58 и № 53 (а; б; в).