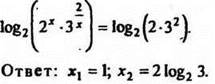Производная показательной функции. Производная логарифмической функции - ОБОБЩАЮЩЕЕ ПОВТОРЕНИЕ КУРСА АЛГЕБРЫ И НАЧАЛ АНАЛИЗА - 2-е полугодие

УРОК № 12

Тема. Производная показательной функции. Производная логарифмической функции

Цели: повторить правила нахождения производных показательной и логарифмической функций; упражнять в решении показательных и логарифмических уравнений и неравенств.

Ход урока

I. Анализ домашней контрольной работы

Указать ошибки, сделанные учащимися в ходе выполнения работы.

II. Выполнение упражнений

1. Запишите формулу производной для функции

2. Решить № 10 и № 11 на стр. 263 -264.

3*. На гиперболе у = 2/x найдите точки, ближайшие к началу координат.

Решение

Пусть М(х;у) -точка, лежащая на гиперболе. Найдём расстояние от точки до начала координат: d2 = х2 + у2; т. к. у = 2/x, то

Рассмотрим функцию

Найдём критические точки функции:

а) f’(x) не имеет смысла в точке х = 0;

Критические точки принадлежат области определения функции:

Рис. 69

При переходе через точки производная меняет знак с минуса на плюс. Следовательно, точки минимума. Минимум функции в этих точках есть её наименьшее значение, т. к. на области определения только две точки минимума. Если то если Ответ: точки гиперболы, ближайшие к началу координат

4. Найти площадь фигуры, ограниченной линиями

Решение

В одной системе координат построим графики функций:

графиком функции является кубическая парабола.

x	-2	-1	0	1	2
.	2	1/4	0	-1/4	-2

у = х + 4

y = 5x

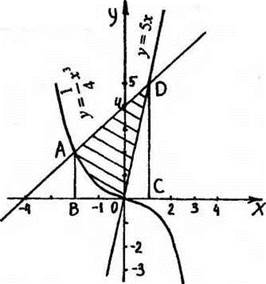
Рис. 70

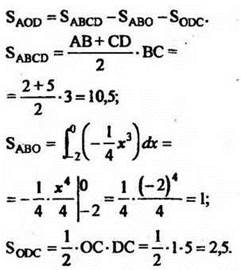
Тогда SAOD = 10,5 - 1 - 2,5 = 7. Ответ: 7.

5. Найти площадь фигуры, ограниченной графиком функции y = sin x, определенной на отрезке [0;], и прямой, проходящей через точки M(/2;1) и N(;0).

Рис. 71

Решение

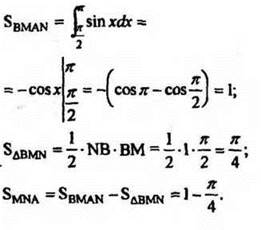
Ответ: 1 - /4.

6. Решить неравенство

Решение

Учитывая область определения логарифмической функции и монотонное убывание функции на всей области определения, перейдем к равносильной системе:

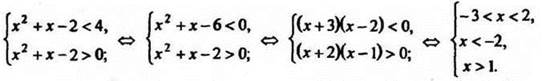
Рис. 72

Решения системы -3 < х < -2 и 1 < х < 2. Ответ: (-3;-2)U(1;2).

7*. Решить неравенство

Решение

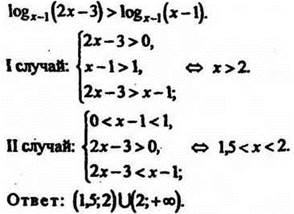
8. Решить уравнение

Решение

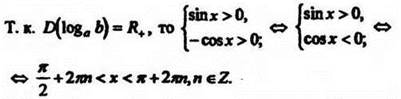
Из равенства логарифмов по одинаковому основанию следует равенство выражений, стоящих под знаком логарифма:

Промежутку принадлежат корни

Можно ответ записать по-другому:

Ответ:

9*. Решите уравнение

Указание. Прологарифмируем обе части уравнения по основанию 2: