Линейная функция и ее график - урок 3 - ІI четверть - Функции

ЦЕЛЬ УРОКА: Вывести условия пересечения и параллельности графиков двух линейных функций.

ПЛАН УРОКА:

№	Этап урока	Содержание	Время (мин)
1	Организационный момент	Нацелить учащихся на урок	1
2	Проверка домашнего задания	Коррекция ошибок	5
3	Устная работа	Актуализация опорных знаний	5
4	Изучение нового материала	Вывести условие пересечения и параллельности графиков двух линейных функций	6
5	Тренировочные упражнения	Формировать умение использовать условие параллельности и пересечения графиков линейных функций при решении задач	18
6	Упражнения на повторение	Повторить составление выражения по условию задачи	6
7	Подведение итогов урока	Обобщить теоретические сведения, полученные на уроке	2
8	Сообщение домашнего задания	Разъяснить содержание домашнего задания	2

ХОД УРОКА

I. Организационный момент.

II. Проверка домашнего задания (фронтально).

III. Актуализация опорных знаний.

Устно:

1) Решить уравнение:

2) Какой из приведенных ниже графиков является графиком функции у = 3х - 6?

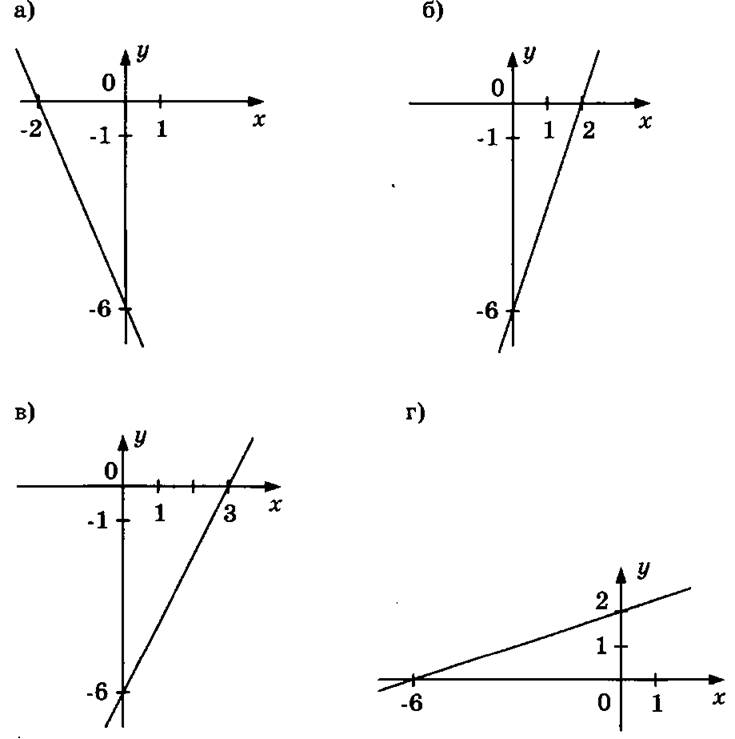
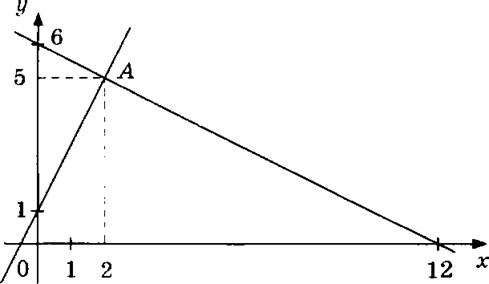
3) На рисунке изображены 2 прямые, пересекающиеся в точке А. Найти координаты точки А.

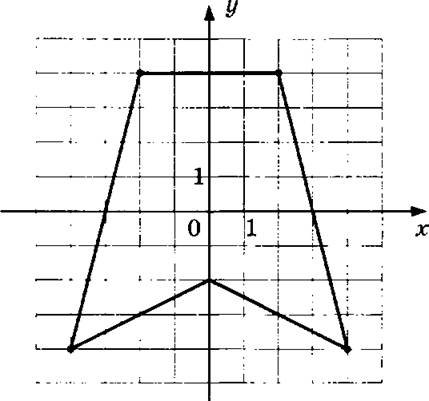
4) Найти координаты вершин многоугольника.

IV. Изучение нового материала.

(п. 16 по учебнику, путем фронтальной беседы)

1) Как выяснить пересекаются ли графики функций, заданных формулами y = 0,9x – 1 и y = 0,8x + 1.

1 способ. Можно продолжить графики до их пересечения в точке и найти координаты этой точки. (Это не всегда удобно, продолжение затруднено.)

2 способ. Чтобы найти координаты точки пересечения графиков, надо:

1. Решить уравнение 0,9x - 1 = 0,8x + 1 и найти х = 20. Это будет абсцисса точки пересечения.

2. Подставив в уравнение любой из данных функции х = 20, найти у = 17. Это — ордината точки пересечения.

(20; 17) — точка пересечения графиков функций у = 0,9x - 1 и у = 0,8x + 1.

2) Как будут вести себя прямые, являющиеся графиками линейных функций с одинаковыми коэффициентами при х? Например, у = 0,5х + 1.5, и у = 0,5x - 2.

На рис. 36 они выглядят параллельными, т.е. не имеющими общих точек. Так ли это?

Решим уравнение 0,5x + 1,5 = 0,5x - 2.

Это уравнение не имеет корней. Следовательно, и прямые, которые являются графиками функций у = 0,5x -Н 1,5 и у = 0,5x - 2 не имеют общих точек, т.е. они параллельны.

3) Читаем правило на с. 73.

4) Вводим понятие углового коэффициента (k) прямой — графика функции у = kx + b и еще раз формулируем условие пересечения и параллельности графиков линейных функций.

5) По рис. 36 рассматриваем взаимное расположение прямых у = kx + b с одинаковыми k и различными значениями b.

6) По рис. 38 разбираем взаимное расположение прямых у = kx + b с различными значениями k и одним и тем же значением b.

V. Тренировочные упражнения.

№№ 369, 370 — на доске и в тетрадях, с подробным объяснением;

№ 371 — самостоятельно с последующей проверкой;

№ 372 (а, б) — на доске и в тетрадях;

№ 372 (в, г) — самостоятельно с последующей проверкой.

VI. Упражнения на повторение.

№ 338 — самостоятельно с последующей проверкой.

VII. Итог урока.

В каком случае графики двух линейных функций пересекаются? Как найти координаты точки пересечения?

В каком случае графики двух линейных функций являются параллельными прямыми?

VIII. Домашнее задание.

п. 16, №№ 373, 311, 296 (б).