Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Натуральные числа. Делимость натуральных чисел - ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ
Данная тема — одна из важнейших тем алгебры. Изучается она, в основном, в 5—6 классах школы и в дальнейшем к ее изучению практически не возвращаются. В то же время на эту тему существует значительное количество самых разнообразных задач, которые часто встречаются на олимпиадах, при поступлении в физико-математические школы и институты. Школьники (и даже старших классов), как правило, большинство задач этой темы, к сожалению, решить не могут. Поэтому остановимся на этом разделе достаточно подробно и рассмотрим те задачи, которые по силам учащимся 8-х классов.
Уроки 27-28. Натуральные числа. Делимость натуральных чисел
Цели: напомнить основные сведения о множестве натуральных чисел и рассмотреть типичные задачи по теме.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала (основные понятия)
Числа, которые используются для счета предметов, называются натуральными: 1, 2, 3, 4, ... Множество натуральных чисел обозначают буквой N. Для того чтобы записать, что какое-либо число принадлежит рассматриваемому множеству, используют знак е. Например, утверждение, что число 5 является натуральным (или что число 5 принадлежит множеству натуральных чисел N), можно записать так: 5 ∈ N. Число 2, 3 не является натуральным. Это можно записать с помощью знака ∉, т. е. 2, 3 ∉ N.
Все натуральные числа (исключая число 1) разделяются на простые числа и составные числа.
Число называется составным, если оно имеет хотя бы один делитель, который не равен самому числу или единице. Например, число 18 имеет такие делители: 2, 3, 6, 9. Поэтому число 18 является составным. (Разумеется, кроме перечисленных делителей у числа 18 есть еще два делителя: 1 и 18).
Число называется простым, если оно не имеет других делителей кроме самого себя и единицы (например, 2, 3, 5, 7, 11, 13, 17, 19, 23, ...).
Число 1 не является ни простым, ни составным.
Напомним основные признаки делимости натуральных чисел.
1. Число делится (без остатка или нацело) на число 2, если его последняя цифра четная или 0. (Напомним, что число 0 не является ни четным, ни нечетным). Например, число 35 634 делится на 2, а число 35 635 — не делится.
2. Число делится на число 3, если сумма его цифр делится на 3. Например, число 33 606 делится на 3, т. к. сумма цифр этого числа 3 + 3 + 6 + 0 + 6 = 18 делится на 3. Число 32 606 имеет сумму цифр 3 + 2 + 6 + 0 + 6 = 17, которая на 3 не делится. Поэтому число 32 606 также на 3 не делится.
3. Число делится на число 4, если две его последние цифры образуют число, которое делится на 4, или являются нулями. Например, число 35 112 делится на 4, т. к. число, образованное двумя последними цифрами (число 12), делится на 4.
Обратите внимание на этот признак делимости. Очень часто школьники ошибочно «сокращают» этот признак делимости до такого: число делится на число 4, если две его последние цифры делятся на 4. Разумеется, данный «признак делимости» является грубой ошибкой. В рассмотренном примере число 35 112 делилось на 4, хотя ни одна из его двух последних цифр (1 и 2) на 4 не делится.
Число 35 118 на число 4 не делится, т. к. число 18 (образованное двумя последними цифрами) на 4 не делится.
4. Число делится на число 5, если его последняя цифра 0 или 5. Например, числа 35 110 и 35 115 делятся на 5, а число 37 513 на 5 не делится.
5. Число делится на число 8, если три его последние цифры образуют число, которое делится на 8, или являются нулями. Например, число 37 408 делится на 8, т. к. число 408 делится на 8. Число 37 414 не делится на 8, т. к. число 414 не делится на 8.
6. Число делится на число 9, если сумма его цифр делится на 9. Например, число 71 505 делится на 9, т. к. сумма цифр этого числа 7 + 1 + 5 + 0 + 5 = 18 делится на 9. Число 70 505 имеет сумму цифр 7 + 0 + 5 + 0 + 5 = 17, которая на 9 не делится. Следовательно, и само число не делится на 9.
7. Число делится на число 10, если его последняя цифра нуль. Например, число 37 510 делится на 10, а число 37 515 не делится на 10.
Признаки делимости позволяют решать и более сложные задачи.
Пример 1
Определите: на какие из чисел 2, 3, 4, 5, 6, 8, 9, 10, 15, 18, 20 делится без остатка число 357 120.
а) Число делится на 2, т. к. его последняя цифра нуль.
б) Число делится на 3, т. к. сумма цифр данного числа равна 3 + 5 + 7 + 1 + 2 + 0 = 18 и делится на 3.
в) Число делится на 4, т. к. две его последние цифры образуют число 20, которое делится на 4.
г) Число делится на 5, т. к. его последняя цифра нуль.
д) Число делится на 6, т. к. 6 = 2 · 3 и из пунктов а, б следует, что число делится на 2 и 3 одновременно.
е) Число делится на 8, т. к. три его последние цифры образуют число 120, которое делится на 8.
ж) Число делится на 9, т. к. сумма его цифр 18 (пункт б) делится на 9.
з) Число делится на 10, т. к. его последняя цифра нуль.
и) Число делится на 15, т. к. оно одновременно делится на 3 и 5 (пункты б, г).
к) Число делится на 18, т. к. из пунктов а, ж следует, что оно делится на 2 и 9.
л) Число делится на 20, т. к. оно одновременно делится на 4 и 5 (пункты в, г).
Заметим, что при рассмотрении делимости числа 357 120 на 6, 15, 18, 20 мы каждое из этих чисел раскладывали на произведение взаимно простых чисел. Напомним, что взаимно простыми числами называются числа, которые не имеют общих делителей. Причем числа могут и не являться простыми. Например, числа 8 и 15 взаимно простые, т. к. не имеют общих множителей. Однако каждое из этих чисел 8 и 15 — составное.
Например, в пункте к число 18 было представлено в виде произведения двух взаимно простых чисел 2 и 9. Затем использовались признаки делимости на эти числа. Если раскладывать число-делитель на произведение не взаимно простых чисел, то решение усложняется, и могут быть допущены ошибки. Например, число 30 не делится на 20 без остатка. Но если представить число 20 в виде 2 · 10, то 30 делится и на 2 и на 10. Однако числа 2 и 10 — не взаимно простые.
Пример 2
Определите, является ли число 98 706 540 321 простым или составным?
Используя признаки делимости, сразу определяем, что данное число на 2, 4, 5, 8, 10 не делится. Теперь разберемся, делится ли это число на 3 и на 9. Найдем сумму цифр этого числа: 9 + 8 + 7 + 0 + 6 + 5 + 4 + 0 + 3 + 2 + 1 = 45. Так как число 45 делится на 3 и на 9, то данное число также делится на 3 и на 9. Так как данное число имеет делители (3 и 9), которые неравны ни единице, ни самому числу, то (по определению) оно является составным.
Нужно заметить, что далеко не всегда одно натуральное число делится на другое без остатка. Например, при делении числа 29 на 3 получаем в частном 9 и в остатке 2. Эту операцию можно записать в виде: 29 = 3 · 9 + 2 или делимое (29) = делитель (3) · частное (9) + остаток (2). При этом остаток должен быть натуральным числом или нулем и меньше, чем делитель.
Пример 3
а) Число 29 можно также записать и в виде: 29 = 3 · 8 + 5. Но в этом случае нельзя считать, что при делении числа 29 на число 3 получается частное 8 и остаток 5, т. к. остаток не может быть больше или равным делителю.
б) Число 29 можно записать и в другом виде: 29 = 3 · 10 + (-1). Но и в этом случае нельзя считать, что при делении числа 29 на число 3 получается частное 10 и остаток (-1), т. к. остаток должен быть натуральным числом.
Таким образом, в общем случае деление с остатком записывается в виде: n = р · k + r. Здесь натуральное число n — делимое, натуральное число р — делитель, натуральное число k — частное, неотрицательное целое число r — остаток (0 ≤ r < р). Если r = 0, то число n нацело (без остатка) делится на число р и n = р · k.
Такая форма записи деления числа с остатком позволяет решать различные задачи.
Пример 4
Число n дает при делении на 13 остаток 5. Какой остаток при делении на 13 дает число вшестеро больше данного?
Если число n дает при делении на 13 остаток 5, то его можно записать в виде: n = 13k + 5, где k — получающееся при этом частное. Тогда число вшестеро большее, т. е. 6n = 6 · (13 · k + 5) = 78 · k + 30. Выделим из числа 6n наибольшее натуральное число, которое без остатка делится на 13, т. е. представим число 6n в виде: 6n = (78k + 26) + 4 = 13 · (6k + 2) + 4. Из этой записи видно, что число 6n при делении на 13 дает в частном число (6k + 2) и остаток 4.
Пример 5
Два числа при делении на 18 дают остаток 9. Доказать, что разность и сумма этих чисел без остатка делятся на 18.
Запишем первое число n в виде: n = 18р + 9 (где р - частное), второе число m в виде: m = 18k + 9 (где k — частное). Рассмотрим теперь разность этих чисел: n – m = (18р + 9) – (18k + 9) = 18р – 18k = 18(р - k).- Эта запись означает, что число (n - m) при делении на 18 дает частное (р - k), а остатка нет (т. е. он равен 0). Поэтому разность чисел n и m без остатка делится на 18.
Найдем сумму чисел n и m: n + m = (18p + 9) + (18k + 9) = 18p + 18k + 18 = 18(p + k + 1). Из такой записи видно, что число (n + m) при делении на 18 дает в частном число (р + k + 1) и остатка нет. Поэтому сумма чисел n и m без остатка делится на 18.
Пример 6
Мальчик раскладывает коллекцию марок. Если он раскладывает по 3 марки, то в конце остается 2 марки. Если он раскладывает по 4 марки, то в конце остается 3 марки. Если он раскладывает по 7 марок, то в конце остается 6 марок. И наконец, если он раскладывает по 11 марок, то в конце остается 10 марок. Какое наименьшее число марок может быть в коллекции?
Легко сообразить, что если бы у мальчика была бы еще одна марка, то раскладывание марок по 3, 4, 7 и 11 штук происходило бы без остатка. Так как числа 3, 4, 7, 11 — взаимно простые (т. е. не имеют общих делителей), то наименьшее число, которое без остатка делится на эти числа - это их произведение. Произведение чисел 3, 4, 7, 11 равно 924. На самом деле у мальчика на одну марку меньше, т. е. 923 марки. Легко проверить, что число 923 при делении на 3 дает остаток 2, при делении на 4 — остаток 3, при делении на 7 — остаток 6 и при делении на 11 — остаток 10, т. е. удовлетворяет условиям задачи.
Итак, наименьшее число марок в коллекции — 923.
Любое натуральное число можно записать в десятичной системе счисления.
Пример 7
а) Число 526 можно записать в виде: 526 = 5 · 100 + 2 · 10 + 6 · 1, из которого следует, что число состоит из пяти сотен, двух десятков и шести единиц.
б) Число ![]() можно записать также в виде:
можно записать также в виде: ![]() = 100 · а + 10 · b + с. Из этой записи видно, что число состоит из а сотен, b десятков и с единиц.
= 100 · а + 10 · b + с. Из этой записи видно, что число состоит из а сотен, b десятков и с единиц.
Заметим, что в записи ![]() черта сверху обязательна, т. к. эта запись означает трехзначное число, у которого первая цифра a, вторая — b и третья — с. Если черта сверху не проставлена, то запись abc означает произведение чисел a, b и с. Поэтому не путайте эти две формы записи. Также отметим, что если число состоит из конкретных цифр (например 729), то черта сверху не нужна: всем понятно, что это число семьсот двадцать девять.
черта сверху обязательна, т. к. эта запись означает трехзначное число, у которого первая цифра a, вторая — b и третья — с. Если черта сверху не проставлена, то запись abc означает произведение чисел a, b и с. Поэтому не путайте эти две формы записи. Также отметим, что если число состоит из конкретных цифр (например 729), то черта сверху не нужна: всем понятно, что это число семьсот двадцать девять.
Рассмотрим теперь примеры на использование записи числа в десятичной системе счисления.
Пример 8
Известно, что шестизначное число ![]() (X — число сотен) делится на 3. Найти цифру X.
(X — число сотен) делится на 3. Найти цифру X.
Используем признак делимости на 3 и найдем сумму цифр данного числа: 1 + 7 + 5 + X + 4 + 6 = 23 + X. Так как число делится на 3, то и сумма его цифр (23 + X) делится на 3. Легко сообразить, что при X = 1 сумма цифр равна 24 и делится на 3; при Х = 4 сумма цифр 27 и делится на 3; при Х = 7 сумма цифр 30 и делится на 3. Следующее число Х = 10 и при этом (23 + X) делится на 3. Но X = 10 — не цифра (0 ≤ X ≤ 9). Поэтому задача имеет только три решения Х = 1, Х = 4, X = 7.
Пример 9
Вывести (доказать) признак делимости на 9.
Рассмотрим, например, трехзначное число А = ![]() , которое можно записать в виде А = 100 · a + 10b + с. В этом числе выделим слагаемые, которые всегда делятся на 9: А = (99а + 9b) + (a + b + с). В этом выражении первое слагаемое (99а + 9b) = 9 · (11а + b) при всех цифрах а и b без остатка делится на 9. Поэтому чтобы делилось на 9 все число А, необходимо, чтобы делилась на 9 оставшаяся часть, т. е. выражение (а + b + с). Легко сообразить, что это выражение - сумма цифр данного числа
, которое можно записать в виде А = 100 · a + 10b + с. В этом числе выделим слагаемые, которые всегда делятся на 9: А = (99а + 9b) + (a + b + с). В этом выражении первое слагаемое (99а + 9b) = 9 · (11а + b) при всех цифрах а и b без остатка делится на 9. Поэтому чтобы делилось на 9 все число А, необходимо, чтобы делилась на 9 оставшаяся часть, т. е. выражение (а + b + с). Легко сообразить, что это выражение - сумма цифр данного числа ![]() . Таким образом, число А делится на 9, если делится на 9 сумма цифр этого числа (т. е. число а + b + с).
. Таким образом, число А делится на 9, если делится на 9 сумма цифр этого числа (т. е. число а + b + с).
Мы доказали этот признак делимости для трехзначного числа А. Разумеется, доказательство останется таким же, если рассмотреть число А, содержащее другое количество цифр.
Заметим, что приведенное доказательство также является и выводом признака делимости на 3.
Пример 10
Найти все пятизначные числа вида ![]() , которые без остатка делятся на 15.
, которые без остатка делятся на 15.
Так как число 15 можно представить в виде: 15 = 3 · 5, то данное число будет делиться на 15, если оно будет делиться и на 3, и на 5. Для делимости на 5 требуется, чтобы последняя цифра числа Y равнялась нулю или пяти (т. е. Y = 0 или Y = 5).
Для делимости на 3 данного числа необходимо, чтобы сумма A его цифр, равная А = 3 + 1 + Х + 7 + Y = 11 + Х + Y, делилась на 9. В случае Y = 0 сумма цифр А = 11 + Х и тогда X может иметь решение Х = 1, Х = 4 и Х = 7. В случае Y = 5 сумма цифр A = 16 + Х и возможны решения: Х = 2, Х = 5 и Х = 8.
Итак, задача имеет шесть решений — это числа: 31170, 31470, 31770, 31275, 31575 и 31875.
Пример 11
Доказать, что если к двузначному числу приписать такое же число, то полученное четырехзначное число кратно 101.
Пусть дано двузначное число с цифрами а и b, т. е. ![]() . Припишем к этому числу такое же и получим четырехзначное число
. Припишем к этому числу такое же и получим четырехзначное число ![]() , которое в десятичной системе имеет вид: 1000 · a + 100 · b + 10 · а + b = 1010a + 101b = 101 · (10а + b). Теперь легко увидеть, что полученное четырехзначное число делится на 101 без остатка.
, которое в десятичной системе имеет вид: 1000 · a + 100 · b + 10 · а + b = 1010a + 101b = 101 · (10а + b). Теперь легко увидеть, что полученное четырехзначное число делится на 101 без остатка.
Как известно, составные натуральные числа могут быть разложены на множители. Часто требуется, чтобы такие множители были простыми числами. Любое составное число можно разложить на произведение простых множителей, причем единственным образом.
Разложение на простые множители начинают с наименьших простых чисел 2, 3, 5, используя признаки делимости. При этом последовательно производят деление данного числа на найденные простые делители. Результаты такого деления удобно записывать «столбиком».
Пример 12
Разложить на простые множители число 9000.

Данное число 9000 по признаку делимости делится на 2. В результате получаем число 4500, которое также делится на 2. Имеем число 2250, которое также делится на 2. Разделив, получаем 1125. По признаку делимости это число делится на 3. Имеем число 375, которое также делится на 3. Разделив, получаем 125. Это число уже на 3 не делится, но делится на 5. Получаем 25. Такое число вновь делится на 5. Имеем 5. Это число является простым и делится только на само себя. Проследив за выполненными действиями (правая часть от вертикальной черты), запишем разложение данного числа на простые множители:
9000 = 2 · 2 · 2 · 3 · 3 · 5 · 5 · 5 или 9000 = 23 · 32 · 53 (здесь учтено понятие степени натурального числа).
В тех случаях, когда данное число имеет другие простые делители (7, 11, 13 и т. д.), признаки делимости уже не помогают. Поэтому приходится проверять, делится ли число на такие числа непосредственным делением.
Пример 13
Разложить на простые множители число 11011.

По признакам делимости это число не делится на 2, 3, 5. Непосредственным делением убеждаемся, что это число делится на следующее простое число 7. Получаем 1573. Это число не делится на 7, но делится на следующее простое число 11. Имеем 143, это число также делится на 11, и получаем 13. Число 13 — простое и делится только само на себя.
После этого выпишем разложение данного числа на простые множители: 11011 = 7 · 11 · 11 · 13 = 7 · 112 · 13.
Для нескольких натуральных чисел a, b, с, ... важнейшими понятиями являются наименьшее общее кратное и наибольший общий делитель этих чисел.
Наименьшим общим кратным (НОК) натуральных чисел a, b, с, ... называется наименьшее натуральное число, которое нацело делится на эти числа а, b, с,...
Для нахождения НОК чисел a, b, с,...:
1) выписывают разложения на простые множители чисел а, b, с, ...;
2) перечисляют все простые множители, входящие хотя бы в одно из этих разложений;
3) каждый из перечисленных множителей возводят в максимальную степень, с которой этот множитель входит в разложения;
4) произведение полученных степеней простых множителей дает НОК чисел a, b, с,...
Пример 14
Найти наименьшее общее кратное чисел 48, 60, 72.
1) Разложим данные числа на простые множители:
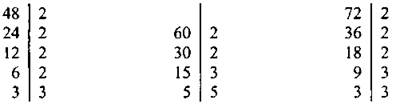
Получаем: 48 = 24 · 3, 60 = 22 · 3 · 5, 72 = 23 · 32.
2) Хотя бы в одно из этих разложений входят числа 2, 3 и 5.
3) Наибольшая степень числа 2 — 4, числа 3 — 2, числа 5 — 1. Поэтому эти множители возведем в такие степени, т. е. 24; 32; 51 (или просто 5).
4) Найдем НОК (48, 60, 72) = 24 · 32 · 5 = 16 · 9 · 5 = 720. Это наименьшее число, которое без остатка делится и на 48, и на 60, и на 72. Легко сделать проверку: 720 : 48 = 15, 720 : 60 = 12, 720 : 72 = 10.
Заметим, что вычисления НОК можно упростить, если учесть разложения данных чисел: НОК = 24 · 32 · 5 = (24 · 3) · 3 · 5 = 48 · 15 = 720. Здесь были сгруппированы множители таким образом, чтобы выделить разложение числа 48 = (24 · 3).
Наибольшим общим делителем (НОД) натуральных чисел a, b, с, ... называется наибольшее натуральное число, на которое делятся нацело числа a, b, с,...
Для нахождения НОД чисел а, b, с,...:
1) выписывают разложения на простые множители чисел а, b, с,...;
2) перечисляют все простые множители, входящие во все разложения;
3) каждый из перечисленных множителей возводят в минимальную степень, с которой этот множитель входит в разложения;
4) произведение полученных степеней этих множителей дает НОД чисел а, b, с,...
Пример 15
Найти наибольший общий делитель чисел 48, 60, 72.
1) Разложения данных чисел возьмем из предыдущего примера: 48 = 24 · 3, 60 = 22 · 3 · 5,72 = 23 · 32.
2) Во все три разложения входят только множители 2 и 3.
3) Наименьшая степень числа 2 — 2, числа 3 — 1. Поэтому эти множители возведем в такие степени, т. е. 22, 31 (или просто 3).
4) Найдем НОД (48, 60, 72) = 22 · 3 = 4 · 3 = 12. Это наибольшее число, на которое нацело делятся числа 48, 60, 72. Сделаем проверку: 48 : 12 = 4, 60 : 12 = 5, 72: 12 = 6.
Понятие НОК и НОД чисел часто используются при решении задач.
Пример 16
Найти все натуральные числа а и b, если НОД (a, b) = 13, НОК (а, b) = 663.
Разложим число 663 на простые множители: 663 = 3 · 13 · 17. Из правил вычисления НОК и НОД следует, что множитель 13 входит в числа а и b. множители 3 и 17 могут входить только в одно из чисел а и b. Поэтому возможны только следующие варианты решения.
а |
13 |
3 · 13 · 17 = 663 |
3 · 13 = 39 |
13 · 17 = 221 |
b |
3 · 13 · 17 = 663 |
13 |
13 · 17 = 221 |
3 · 13 = 39 |
Итак, возможны четыре решения: а = 13 b = 663, а = 663 b = 13, а = 39 b = 221, a = 221 b = 39.
Заметим, что для двух чисел а и b всегда выполняется равенство НОД (а, b) · НОК (a, b)= 13 · 663 = 8619. Для а = 39, b = 221 также получаем а · b = 39 · 221 = 8619. Это же справедливо и для других пар чисел а и b из этого примера.
Пример 17
Солдаты выстроились в ряды по 12 человек в каждом, а затем перестроились по 8 человек в ряду. Сколько было солдат, если их больше 180, но меньше 200?
Очевидно, что число солдат было таким, что оно без остатка делилось на 12 и на 8, т. е. это число или НОК (12, 8) или число, которое отличается от НОК в натуральное число раз. Поэтому прежде всего найдем НОК (12, 8) = 24.
Так как число солдат было значительно больше, то это число кратно 24, т. е. равно 24 · n (где n — натуральное число). Легко подобрать подходящее n = 8. Тогда 24 · n = 24 · 8 = 192. Это число солдат удовлетворяет всем условиям задачи: их число больше 180, но меньше 200. Кроме того, при построении в ряды по 12 человек получается 16 рядов, при построении по 8 человек получается 24 ряда.
Итак, солдат было 192 человека. .
Пример 18
На базу прибыло три состава цистерн с нефтью: в первом составе было 360 т нефти, во втором — 432 т, в третьем — 792 т. Сколько цистерн было в каждом составе, если в каждой цистерне одинаковое и целое число тонн нефти и это число больше 50?
Очевидно, что в цистерне должно быть такое число тонн, чтобы оно было общим делителем чисел 360,432 и 792. Разложим эти числа на простые множители:
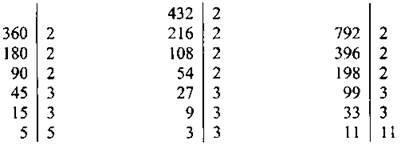
Легко увидеть, что общими делителями данных чисел являются числа: 2, 3, 4, 6, 8, 9, 12, 18, 24, 36, 72. Из них только число 72 удовлетворяет условию задачи. Отметим, что число 72 = НОД (360, 432, 792). Легко проверить, что в первом составе было 360 : 72 = 5 цистерн, во втором — 432 : 72 = 6 цистерн, в третьем — 792 : 72 = 11 цистерн.
Итак, в каждой цистерне 72 тонны.
III. Задание на уроке и на дом
1. Определите, на какие из чисел 2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 18, 20 без остатка делится число:
а) 55440; б) 145860; в) 102102; г) 435435; д) 178932; е) 63240.
Ответы: а) 2; 3; 4; 5; 6; 8; 9; 10; 12; 15; 18; 20; б) 2; 3; 4; 5; 6; 10; 12; 15; в) 2; 3; 6; г) 3; 5; 15; д) 2; 3; 4; 6; 12; е) 2; 3; 4; 5; 6; 8; 10; 12; 15.
2. Докажите, что число является составным: а) 54 321; б) 54 213; ![]() ж) 1072 - 1; з) 1037 - 1; и) 10068 - 1; к) 100031 - 1; л) 1053 - 7; м) 1039 - 7.
ж) 1072 - 1; з) 1037 - 1; и) 10068 - 1; к) 100031 - 1; л) 1053 - 7; м) 1039 - 7.
Указание: используйте признаки делимости на 3 и 9.
3. Определите цифру X, если число
а) ![]() кратно 4.
кратно 4.
б) ![]() делится на 4.
делится на 4.
в) ![]() кратно 3;
кратно 3;
г) ![]() кратно 3.
кратно 3.
д) ![]() кратно 18.
кратно 18.
е) ![]() делится на 45;
делится на 45;
ж) ![]() кратно 8.
кратно 8.
з) ![]() делится на 8.
делится на 8.
и) ![]() кратно 24.
кратно 24.
к) ![]() делится на 24.
делится на 24.
Ответы: а) 0; 4; 8; б) 2; 6; в) 2; 5; 8; г) 2; 5; 8; д) 3; е) 1; ж) 3; 7; з) 0; 2; 4; 6; 8; и) 2; 8; к) 2 (указание: использовать соответствующие признаки делимости).
4. Определите цифры Х и Y, если число
а) ![]() кратно 15.
кратно 15.
б) ![]() делится на 12.
делится на 12.
в) ![]() кратно 18;
кратно 18;
г) ![]() делится на 45.
делится на 45.
д) ![]() кратно 36.
кратно 36.
е) ![]() делится на 20.
делится на 20.
Ответы: а) Y = 0 X = 1; 4; 7; Y = 5 X = 2; 5; 8 (учесть признаки делимости на 3 и 5);
б) Y = 2 X = 2; 5; 8; Y = 6 Х = 1; 4; 7 (учесть признаки делимости на 3 и 4);
в) Y = 0 Х = 8; Y = 2 Х = 6; У = 4 Х = 4; Y = 6 Х = 2; Y = 8 Х = 0; 9 (учесть признаки делимости на 2 и 9);
г) Y = 0 Х = 7; Y = 5 Х = 2 (учесть признаки делимости на 5 и 9);
д) Y = 2 Х = 6; Y = 4 Х = 4 (учесть признаки делимости на 4 и 9);
е) Y = 0 Х = 0; 2; 4; 6; 8 (учесть признаки делимости на 4 и 5).
5. Докажите, что
а) если а кратно 3, b кратно 5, то 5a + 3b кратно 15;
б) если а кратно 4, b кратно 7, то 7а + 7b кратно 28;
в) если а кратно 2, b кратно 5, то 5а — 2b кратно 10;
г) если а кратно 6, b кратно 7, то 7а — 6b кратно 42.
6. Число а при делении на 11 дает остаток 3. Найти остаток при делении на 11 числа
а) 5а; б) 4а + 3; в) а2; г) а2 + 5; д) а2 + 2а; е) а3.
Ответы: а) 4; б) 4; в) 9; г) 3; д) 4; е) 5 (указание: число а запишите в виде а = 11k + 3, где k — частное).
7. Число а при делении на 24 дает остаток 9. Найти остаток от деления числа а на
а) 2; б) 3; в) 4; г) 6; д) 8; е) 12.
Ответы: а) 1; б) 0; в) 1; г) 3; д) 1; е) 9 (указание: число а запишите в виде а = 24k + 9. Тогда:
а) а = 2 · (12k + 4) + 1, т. е. число а при делении на 2 дает остаток 1;
б) а = 3 · (8k + 3), т. е. число а кратно 3 (остаток равен 0);
в) а = 4 · (6k + 2) + 1, т. е. число а при делении на 4 дает остаток 1;
г) а = 6 · (4k + 1) + 3, т. е. число а при делении на 6 дает остаток 3;
д) а = 8 · (3k + 1) + 1, т. е. число а при делении на 8 дает остаток 1;
е) а = 12 · 2k + 9, т. е. число а при делении на 12 дает остаток 9).
8. Найти все числа, которые при делении на 3 дают остаток 1, а при делении на 5 дают остаток 3. Найти остаток от деления таких чисел на 15.
Ответ: 15р + 13, где p — целое; 13 (указание: числа, которые при делении на 3 дают остаток 1, имеют вид 3k + 1. Числа, которые при делении на 5, дают остаток 3, имеют вид 5n + 3. Очевидно, что 3k + 1 = 5n + 3. Выразим ![]() . При этом n и k должны быть целыми числами. Например, при k = 4 получим целое
. При этом n и k должны быть целыми числами. Например, при k = 4 получим целое ![]() Легко сообразить, что все целые k, удовлетворяющие условию
Легко сообразить, что все целые k, удовлетворяющие условию ![]() , имеют вид k = 4 + 5р (где р — целое число). Тогда искомое число 3k + 1 = 3(4 + 5р) + 1 = 15р + 13, т. е. при делении на 15 дает остаток 13.
, имеют вид k = 4 + 5р (где р — целое число). Тогда искомое число 3k + 1 = 3(4 + 5р) + 1 = 15р + 13, т. е. при делении на 15 дает остаток 13.
9. Найти все числа, которые при делении на 4 дают остаток 3, а при делении на 6 дают остаток 1. Найти остаток от деления таких чисел на 2, 3, 12.
Ответ: 12р + 7, где р — целое; остатки 1; 1; 7 соответственно (указание: числа, которые при делении на 4 дают остаток 3, имеют вид 4k + 3. Числа, которые при делении на 6 дают остаток 1, имеют вид 6n + 1. Очевидно, что 4k + 3 = 6n + 1. Выразим ![]() При этом n и k должны быть целыми числами. Например, при n = 1 получим целое
При этом n и k должны быть целыми числами. Например, при n = 1 получим целое ![]() Легко сообразить, что все целые n, удовлетворяющие условию
Легко сообразить, что все целые n, удовлетворяющие условию ![]() имеют вид n = 1 + 2р (где р — целое число). Тогда искомое число 6n + 1 = 6(1 + 2р) + 1 = 12р + 7. Аналогично задаче 7 легко установить, что это число при делении на 2 дает остаток 1, при делении на 3 — тоже остаток 1, при делении на 12 — остаток 7).
имеют вид n = 1 + 2р (где р — целое число). Тогда искомое число 6n + 1 = 6(1 + 2р) + 1 = 12р + 7. Аналогично задаче 7 легко установить, что это число при делении на 2 дает остаток 1, при делении на 3 — тоже остаток 1, при делении на 12 — остаток 7).
10. Разложите на простые множители и найдите НОК и НОД чисел:
а) 648 и 108; б) 10125 и 675; в) 3780 и 1800; г) 300 и 4410.
Ответы: а) 648 = 23 · 34, 108 = 22 · 34, НОК = 23 · 34 = 648, НОД = 22 · 33 = 108;
б) 10125 = 34 · 53, 675 = 33 · 52, НОК = 34 · 53 = 10125, НОД = 33 · 52 = 675;
в) 3780 = 22 · 33 · 5 · 7, 1800 = 23 · 32 · 52, НОК = 23 · 33 · 52 · 7 = 37800, НОД = 22 · 32 · 5 = 180;
г) 300 = 22 · 3 · 52, 4410 = 2 · 32 · 5 · 72, НОК = 22 · 32 · 52 · 72 = 44100, НОД = 2 · 3 · 5 = 30.
IV. Контрольные вопросы
1. Какие числа называются натуральными? Как обозначается множество натуральных чисел?
2. Простые и составные числа. Приведите примеры.
3. Признаки делимости натуральных чисел.
4. Докажите признаки делимости натуральных чисел.
5. Деление числа с остатком.
6. Наименьшее общее кратное натуральных чисел.
7. Правило нахождения НОК чисел.
8. Наибольший общий делитель натуральных чисел.
9. Правило нахождения НОД чисел.
10. Запись числа в десятичной системе счисления. Приведите примеры.
V. Подведение итогов урока