Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Рациональные числа - ДЕЙСТВИТЕЛЬНЫЕ ЧИСЛА - КВАДРАТНЫЕ КОРНИ
Цель: дать понятие о множестве рациональных чисел.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (самостоятельная работа).
Вариант 1
1. Найти целочисленные решения уравнения:
a) (2x – 3)(6 - 2x)(3x + 8) = 0;
б) ху - 2х + 4у = 11.
2. Докажите, что уравнение не имеет целых корней:
а) 5х2 – 15x - 301 = 0; .
б) 9х + 18у = 736.
Вариант 2
1. Найти целочисленные решения уравнения:
а) (5х + 2)(8 - 4х)(3х - 7) = 0; .
б) ху + 5х - 3у = 17.
2. Докажите, что уравнение не имеет целых корней:
а) 5х2 + 20х - 423 = 0; .
б) 11х - 33у = 641.
III. Изучение нового материала (основные понятия)
Обыкновенной дробью называется число вида m/n (где m — целое число, а n — натуральное). Например: ![]() — обыкновенные дроби. Число m называют числителем дроби, а число n — знаменателем дроби. Всякое целое число можно также рассматривать как обыкновенную дробь со знаменателем 1. Например:
— обыкновенные дроби. Число m называют числителем дроби, а число n — знаменателем дроби. Всякое целое число можно также рассматривать как обыкновенную дробь со знаменателем 1. Например: ![]()
Напомним основное свойство дробей: если числитель и знаменатель данной дроби умножить или разделить на одно и то же (не равное нулю) число, то получится дробь, равная данной дроби.
Пример 1
Рассмотрим дробь 9/15. Умножим ее числитель и знаменатель на число 2. Получаем дробь ![]() Эта дробь равна данной.
Эта дробь равна данной.
Разделим теперь числитель и знаменатель дроби 9/15 на число (-3). Получаем дробь ![]() Эта дробь также равна данной. Итак, имеем:
Эта дробь также равна данной. Итак, имеем: ![]() Поэтому одну и ту же дробь можно представить в виде m/n разными способами.
Поэтому одну и ту же дробь можно представить в виде m/n разными способами.
Обыкновенная дробь m/n называется правильной, если |т| < n, и неправильной, если |m| ≥ n.
Пример 2
а) Дробь 1/3 — правильная, т. к. |1| = 1 < 3.
б) Дробь -7/15 - правильная, т. к. |-7| = -(-7) = 7 < 15.
в) Дробь 9/8 — неправильная, т. к. |9| = 9 > 8.
г) Дробь -5/5 — неправильная, т. к. |-5| = -(-5) = 5.
д) Дробь -11/3 — неправильная, т. к. |-11| = -(-11) = 11 > 3.
Неправильная дробь может быть записана в виде смешанной дроби, т. е. дроби, содержащей целую и дробную части. Например, ![]()
![]()
Рассмотрим более сложные задачи этого раздела.
Пример 3
При каких целых значениях а дробь ![]() будет целым числом? Найти такие числа А.
будет целым числом? Найти такие числа А.
Выделим в числе А такое слагаемое в числителе, которое без остатка делится на знаменатель: ![]()
Чтобы дробь А стала целым числом, необходимо, чтобы дробь ![]() стала целым числом. Так как а — целое число, то и число (а + 3) — целое. Поэтому (а + 3) должно быть делителем числа 2. Число 2 имеет делители ±1 и ±2. Поэтому необходимо рассмотреть четыре случая:
стала целым числом. Так как а — целое число, то и число (а + 3) — целое. Поэтому (а + 3) должно быть делителем числа 2. Число 2 имеет делители ±1 и ±2. Поэтому необходимо рассмотреть четыре случая:
а) а + 3 = 1, откуда а = -2 и ![]()
б) a + 3 = -1, откуда а = -4 и ![]()
в) а + 3 = 2, откуда а = -1 и ![]()
г) а + 3 = -2, откуда а = -5 и ![]()
Пример 4
Доказать, что сумма двух обыкновенных дробей также является обыкновенной дробью.
Запишем одну дробь в виде m/n, вторую — в виде a/b (где m, a — целые числа; n, b — натуральные числа). Теперь найдем сумму этих дробей: ![]() Таким образом, сумму дробей удалось представить в виде M/N, где числитель M = mn + na является целым числом (как произведение натуральных и целых чисел mb и nа и их сумма), знаменатель N = nb является натуральным числом (как произведение натуральных чисел n и b).
Таким образом, сумму дробей удалось представить в виде M/N, где числитель M = mn + na является целым числом (как произведение натуральных и целых чисел mb и nа и их сумма), знаменатель N = nb является натуральным числом (как произведение натуральных чисел n и b).
Таким образом, сумма двух обыкновенных дробей является обыкновенной дробью.
Любую обыкновенную дробь можно записать в виде десятичной дроби, разделив «уголком» ее числитель на знаменатель.
Пример 5
Обратить в десятичную дробь: а) 3/40, б) 59/110.

В случае а) была получена конечная десятичная дробь: 3/40 = 0,075. В случае б) легко увидеть, что после выполненного деления вновь получается остаток 40, и процесс деления будет неограниченно продолжаться (отмечено скобкой справа). Поэтому получаем: ![]() бесконечную периодическую десятичную дробь. При этом повторяющаяся группа цифр называется периодом. Принято период указывать в скобках:
бесконечную периодическую десятичную дробь. При этом повторяющаяся группа цифр называется периодом. Принято период указывать в скобках: ![]()
Учитывая, что конечная десятичная дробь не изменится, если после последней цифры записать любое количество нулей (например, 0,075 = 0,0750 = 0,07500 и т. д.), конечные десятичные дроби можно рассматривать как бесконечные периодические десятичные дроби с периодом нуль (например, 0,075 = 0,075(0)). Однако заметим, что период нуль никогда не указывается.
Таким образом, любая обыкновенная дробь m/n может быть представлена единственным образом в виде бесконечной периодической десятичной дроби.
Справедливо также и обратное утверждение: любая бесконечная периодическая десятичная дробь может быть представлена единственным образом в виде обыкновенной дроби m/n .
На примере рассмотрим, как производится такое обращение.
Пример 6
Обратить в обыкновенную дробь: а) 1,6; б) 1,(15).
а) Сразу запишем данную дробь в виде обыкновенной и выполним сокращение: ![]()
б) Обозначим данное число буквой х = 1,(15) = 1,1515... Так как период этой дроби содержит две цифры, то умножим число х на 102 = 100 и получим 100x = 115,1515... Теперь найдем разность чисел 100х и х: 100x - x = 99x = 115,1515... - 1,1515... = 114. Для нахождения х получаем уравнение: 99x = 114, откуда ![]()
Проверить полученные результаты очень просто: надо опять обратить полученные обыкновенные дроби в десятичные:
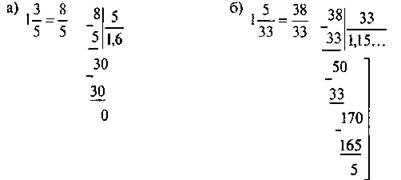
К сожалению, операции над бесконечными периодическими десятичными дробями выполнить намного сложнее. Самый простой способ решения таких задач: перевести эти дроби в обыкновенные и выполнить действия с ними.
Пример 7
Вычислить (1,(3) - 1,(6)): 0,(21).
а) х = 1,(3) = 1,333... Умножим это число на 10 и получим: 10х = 13,333... Тогда 10х - х = 9х = 13,333...- 1,333...= 12. Имеем 9х = 12 и ![]()
б) х = 1,(6) = 1,666... Умножим и это число на 10: 10x = 16,666... Получаем 10х - х = 9х = 16,666...— 1,666... = 15. Имеем 9х = 15 и ![]()
в) х = 0,(21) = 0,2121... Умножим это число на 100 и получим: 100х = 21,2121... Тогда 100х - х = 99х = 21,2121...- 0,2121... = 21, откуда 99х = 21 и ![]()
Теперь запишем этот пример для полученных обыкновенных дробей: ![]()
Таким образом, получаем дробь ![]()
В заключение этого урока сделаем основной вывод: к рациональным числам относятся: целые числа, обыкновенные дроби, конечные десятичные дроби и бесконечные десятичные дроби. Все рациональные числа можно представить в виде m/nт (где m — целое число, n — натуральное число). Множество рациональных чисел обозначают буквой Q.
Заметим, что разные бесконечные десятичные периодические дроби представляют разные рациональные числа. Исключением являются дроби с периодом 9, которые считают другой записью дробей с периодом 0.
Пример 8
а) 2,(9) = 2,99... = 3,00... = 3; б) 2,37(9) = 2,3799... = 2,3800... = 2,38. Бесконечные десятичные дроби с периодом 9 заменяют дробями с периодом 0. При обращении обыкновенной дроби в десятичную не может получиться дробь с периодом 9.
IV. Контрольные вопросы
1. Какие числа относятся к рациональным?
2. В каком виде записываются рациональные числа?
3. Как обозначают множество рациональных чисел?
V. Задание на уроке
№ 255; 257; 259 (а, в, д, ж, и); 260 (б, в, г); 261 (а б, в); 264 (а, в).
VI. Задание на дом
№ 253; 254; 256; 258; 259 (б, г, е); 260 (а, д); 261 (г-е); 262 (а, б); 263.
VII. Творческие задания
1. Докажите, что сумма, разность, произведение, частное двух рациональных чисел также является рациональным числом.
2. Запишите десятичную дробь в виде обыкновенной дроби: а) 1,(3); б) 2,(7); в) -3,(16); г) -5,(28); д) 6,5(21); е) 7,1(27); ж) 4,(163); з) 5,(234).
Ответы: ![]()
![]()
![]()
Решение:
а) Обозначим х = 1,(3), тогда 10x = 13,(3) и 10x - х = 13,(3) - 1,(3) = 12, или 9х = 12, откуда х = 4/3;
б) Обозначим х = 2,(7), тогда 10х = 27,(7) и 10х - х = 27,(7) - 2,(7) или 9х = 25, откуда х = 25/9;
в) Обозначим х = 3,(16), тогда 100х = 316,(16) и 100х – х = 316,(16) - 3,(16) или 99х = 313, откуда х = 313/99;
г) Обозначим х = 5,(28), тогда 100x = 528,(28) и 100х - х = 528,(28) - 5,(28) или 99х = 523, откуда х = 523/99;
д) Обозначим х = 6,5(21), тогда 1000x = 6521,(21) и 10х = 65,(21). Найдем 1000х - 10х = 6521,(21) - 65,(21) или 990х = 6456, откуда х = 6456/990;
е) Обозначим х = 7,1(27), тогда 1000х = 7127,(27) и 10х = 71,(27). Найдем 1000х - 10х = 7127,(27) - 71,(27) = 7056, откуда х = 7056/990;
ж) Обозначим х = 4,(163), тогда 1000х = 4163,(163). Найдем 1000х - х = 4163,(163) - 4,(163) или 999х = 4159, откуда х = 4159/999;
з) Обозначим х = 5,(234), тогда 1000х = 5234,(234). Найдем 1000х - х = 5234,(234) - 5,(234) или 999х = 5229, откуда х = 5229/999;
3. Выполните действия:

Ответы: ![]()
VIII. Подведение итогов урока