Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Квадратный корень из произведения и дроби - СВОЙСТВА АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ - КВАДРАТНЫЕ КОРНИ
Цель: рассмотреть свойства квадратного корня из произведения и дроби.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Перечислите основные свойства функции ![]() и нарисуйте ее график. .
и нарисуйте ее график. .
2. Сравните числа: ![]()
3. Расположите числа в порядке возрастания: ![]()
4. В какой точке график функции ![]() пересекает прямая у = -2х - 1 (если они пересекаются)?
пересекает прямая у = -2х - 1 (если они пересекаются)?
Вариант 2
1. Перечислите основные свойства функции у = х2 и нарисуйте ее график.
2. Сравните числа: ![]()
3. Расположите числа в порядке убывания: ![]()
4. В какой точке график функции ![]() пересекает прямая у = -3х - 2 (если они пересекаются)?
пересекает прямая у = -3х - 2 (если они пересекаются)?
III. Изучение нового материала (основные понятия)
Теорема: корень из произведения неотрицательных множителей равен произведению корней из этих множителей, т. е. ![]() (где a ≥ 0 и b ≥ 0). Докажем это утверждение. Для этого покажем, что выполняются два условия:
(где a ≥ 0 и b ≥ 0). Докажем это утверждение. Для этого покажем, что выполняются два условия:
![]()
Так как a ≥ 0 и b ≥ 0, то каждое из выражений ![]() имеет смысл. По определению арифметического квадратного корня выражения
имеет смысл. По определению арифметического квадратного корня выражения ![]() принимают только неотрицательные значения. Поэтому произведение
принимают только неотрицательные значения. Поэтому произведение ![]() неотрицательно.
неотрицательно.
Используя свойство степени произведения, имеем: ![]()
![]() Таким образом, мы показали, что выполняются условия 1) и 2). Значит, при любых неотрицательных значениях а и b по определению арифметического квадратного корня выполняется равенство
Таким образом, мы показали, что выполняются условия 1) и 2). Значит, при любых неотрицательных значениях а и b по определению арифметического квадратного корня выполняется равенство ![]()
Пример 1
Найдем значение выражения:
![]()
а) Используем теорему о корне из произведения: ![]()
![]()
б) Представим подкоренное выражение в виде произведения множителей, каждый из которых является квадратом целого числа. Применим также теорему о корне из произведения. Имеем: ![]()
![]()
в) В подкоренном выражении разложим разность квадратов чисел на множители и используем теорему о корне из произведения. Получаем: ![]()
Доказанная теорема справедлива и в случае, когда число множителей в подкоренном выражении больше двух. Докажем это утверждение, например, для трех множителей a ≥ 0, b ≥ 0 и с ≥ 0. Получаем: ![]()
![]()
Пример 2
Еще раз вернемся к примеру 16) и получим: ![]()
![]()
Рассмотрим теперь арифметический квадратный корень из дроби. Теорема: корень из дроби, числитель которой неотрицателен, а знаменатель положителен, равен отношению корня из числителя к корню из знаменателя, т. е. ![]() (где а ≥ 0 и b > 0). Докажем это утверждение. Для этого покажем, что выполняются два условия: 1)
(где а ≥ 0 и b > 0). Докажем это утверждение. Для этого покажем, что выполняются два условия: 1) 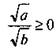 и 2)
и 2) 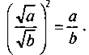
Так как а ≥ 0 и b > 0, то каждое из выражений 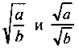 имеет смысл. По определению арифметического квадратного корня выражение
имеет смысл. По определению арифметического квадратного корня выражение ![]() принимает только неотрицательные значения, а выражение
принимает только неотрицательные значения, а выражение ![]() — только положительные значения. Поэтому дробь
— только положительные значения. Поэтому дробь ![]() неотрицательна.
неотрицательна.
Используя свойства степени дроби, имеем 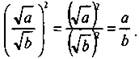 Таким образом, мы показали, что выполняются условия 1) и 2). Значит, при любых неотрицательных значениях а и положительных значениях b по определению арифметического квадратного корня выполняется равенство
Таким образом, мы показали, что выполняются условия 1) и 2). Значит, при любых неотрицательных значениях а и положительных значениях b по определению арифметического квадратного корня выполняется равенство ![]()
Пример 3
Найдем значение выражения ![]()
По теореме о корне из дроби имеем: ![]()
Разумеется, можно сочетать теоремы о корне из произведения и корне из дроби.
Пример 4
Найдем значение выражения ![]() .
.
Используя указанные теоремы, получим: 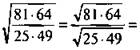
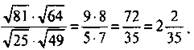
Рассмотренные теоремы справедливы для любых выражений (числовых и алгебраических).
Пример 5
Упростим выражение ![]()
Используя теоремы о корне из произведения и корне издроби, получим 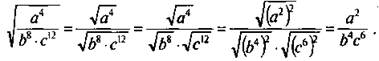
Тождества 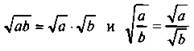 также удобно использовать, поменяв их части местами:
также удобно использовать, поменяв их части местами: 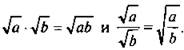
Пример 6
Найдем произведение ![]()
Получаем: ![]()
Пример 7
Найдем частное 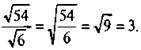
Пример 8
Найдем значение выражения 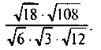
Используя рассмотренные тождества, получим: ![]()
![]()
Пример 9
Упростим выражение 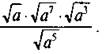
По смыслу задачи переменная a > 0. Получаем: 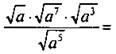
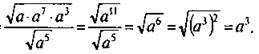
IV. Контрольные вопросы
1. Сформулируйте и запишите теорему о квадратном корне из произведения чисел.
2. Сформулируйте и запишите теорему о квадратном корне из дроби.
V. Задание на уроке
№ 357 (а, д); 358 (а, е); 360 (д); 363 (б); 365 (е); 371 (а, д); 372 (в); № 373 (в).
VI. Задание на дом
№ 357 (е); 358 (в, д); 360 (е); 363 (г); 365 (д); 371 (б, в); 372 (д, з); 373 (д).
VII. Подведение итогов урока