Вынесение множителя из-под знака корня. Внесение множителя под знак корня - ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ - КВАДРАТНЫЕ КОРНИ

Цель: рассмотреть и отработать вынесение множителя из-под знака корня и внесение множителя под знак корня.

Ход урока

I. Сообщение темы и цели урока

II. Изучение нового материала (основные понятия)

Для сравнения числовых выражений, преобразования иррациональных выражений и т. д. необходимы навыки вынесения множителя из-под знака корня и внесения множителя под знак корня, основанные на использовании свойств квадратного корня. Рассмотрим эти приемы на примерах.

Пример 1

Сравним значение выражений Это можно сделать двумя способами.

1 способ (вынесение множителя из-под знака корня). Преобразуем первое иррациональное число √75. Представим число 75 в виде произведения двух множителей, один из которых является квадратом натурального числа: 75 = 25 · 3. Используем теорему о корне из произведения и получим: Теперь легко сравнить данные числа. Так как

При решении число √75 было заменено произведением двух множителей 5 и √3, один из которых — целое число 5, а другое — иррациональное число √3. Такое преобразование называют вынесением множителя из-под знака корня.

2 способ (внесение множителя под знак корня). Теперь преобразуем второе иррациональное число 6√3, представив его в виде арифметического квадратного корня. Для этого число 6 заменим выражением √36 и используем теорему о корне из произведения: Сравним данные числа. Так как 75 < 108, то или

При решении выражение 6√3 было представлено в виде арифметического квадратного корня √108. Такое преобразование называют внесением множителя под знак корня.

Эти способы используются и при решении более сложных задач.

Пример 2

Упростим выражение

В данном выражении вынесем множители из-под знаков корня. Для этого подкоренные выражения представим в виде произведений квадратов натуральных чисел и числа 2, т. е. 50 = 25 · 2 = 52 · 2, 8 = 4 · 2 = 22 · 2 и 32 = 16 · 2 = 42 · 2. Тогда данное выражение имеет вид:

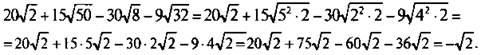Было учтено, что все слагаемые являются подобными членами, т. к. содержат выражения √2 с разными коэффициентами. Итак, данное выражение равно иррациональному числу √2 = -1,41.

Пример 3

Докажем, что выражение равно натуральному числу 2.

В выражении А изменим порядок умножения и внесем величину под знак корня. Получаем:

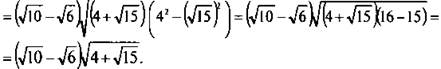
Была использована формула разности квадратов. Теперь внесем под знак корня величину Имеем:

Были использованы формула квадрата разности и вновь формула разности квадратов. Итак, данное выражение действительно равно натуральному числу 2.

Теперь рассмотрим применение этих способов в выражениях с переменными.

Пример 4

Вынесем множитель из-под знака корня в выражении .

Выражение имеет смысл только при a ≥ 0 (если a < 0, то и а3 < 0). Представим подкоренное выражение а3 в виде произведения а2 · а, в котором множитель а2 является степенью с четным показателем. Тогда, учитывая свойства квадратного корня, получаем: При этом было учтено, что а ≥ 0 и |а| = а.

Пример 5 .

Вынесем множитель из-под знака корня в выражении .

Выражение имеет смысл только при -а7 ≥ 0 (или а7 ≤ 0), т. е. a ≤ 0. Представим подкоренное выражение -а7 в виде произведения а6 · (-а), в котором первый множитель а6 является степенью с четным показателем, а второй множитель (-а) принимает только неотрицательные значения. Тогда получаем: Было учтено, что а3 ≤ 0 и |а3| = -а3.

Пример 6

Внесем множитель под знак корня в выражении

Отрицательный множитель нельзя представить в виде арифметического квадратного корня и поэтому такой множитель нельзя внести под знак корня. Поэтому внесем под знак корня положительный множитель 5. Получаем: Данное и полученное выражения имеют смысл только при х ≥ 0.

Пример 7

Внесем множитель под знак корня в выражении

Множитель а может быть любым числом (положительным, нулем или отрицательным). Поэтому надо рассмотреть два случая:

если a ≥ 0, то |а| = а и выражение имеет вид:

если а < 0, |а| = -а или а = -|а| и выражение имеет вид Итак, данное выражение равно при а ≥ 0 и равно при а < 0. Обратите внимание, что результат существенно зависит от величины переменной а.

Пример 8

Упростим выражение .

Учтем, что знаменатель подкоренного выражения является квадратом разности. Получаем: 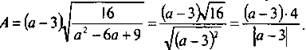Раскроем знак модуля, рассмотрев два случая:

а) если а > 3, то а - 3 > 0 и |а - 3| = а - 3, данное выражение равно

б) если а < 3, то а - 3 < 0 и |a - 3| = -(а - 3), данное выражение равно

Итак, выражение А = 4 при а > 3; А = -4 при а < 3. При а = 3 выражение А не имеет смысла. И вновь результат существенно зависит от величины переменной а.

III. Задание на уроке

№ 401 (в); 402 (a); 404 (а, в); 405 (в); 407 (б, г); 408 (а); 409 (а, б); 410 (а); 412 (а, б).

IV. Задание на дом

№ 401 (е); 402 (г); 404 (б, д); 405 (г); 407 (в, д); 408 (б); 409 (б, г); 410 (б); 412 (б, е).

V. Подведение итогов урока