Итоги контрольной работы - урок 4 - ПРИМЕНЕНИЕ СВОЙСТВ АРИФМЕТИЧЕСКОГО КВАДРАТНОГО КОРНЯ - КВАДРАТНЫЕ КОРНИ

Целы: сообщить результаты работы, рассмотреть наиболее типичные ошибки, разобрать трудные задачи.

Ход урока

I. Сообщение темы и цели урока

II. Итоги контрольной работы

1. Распределение работ по вариантам и результатам решения. Данные о результатах работы удобно заносить в таблицу (для каждой пары вариантов).

№ задачи Итоги	1	2	3	...	6
+	5
±	1
—	1
Ø	1

Обозначения:

+ — число решивших задачу правильно или почти правильно.

± — число решивших задачу со значительными ошибками; .

— — число не решивших задачу;

Ø — число не решавших задачу. Вариант 1, 2 — 8 учеников.

2. Типичные ошибки, возникшие при решении задач.

3. Наиболее трудные задачи и их разбор (учителем или школьниками, сделавшими эту задачу).

4. Разбор всей контрольной работы (вывесить на стенде ответы к заданиям вариантов и разбор наиболее трудных вариантов).

III. Ответы и решения

Вариант 1

1. Ответ: 14 – 4√6.

2. Ответ: А < В.

3. Ответ: -√а - 3 (при а ≥ 0, а ≠ 9).

4. Ответ: 2 + √10.

5. Ответ: -2/11.

6. Ответ: прямая у = 1 - х при х ≤ 1.

Вариант 2

1. Ответ: 21 - 6√6.

2. Ответ: А > В.

3. Ответ: -√с - 4 (при с ≥ 0, с ≠ 16).

4. Ответ: 5 + √15.

5. Ответ: -1/22.

6. Ответ: прямая у = х - 2 при х ≥ 2.

Вариант 3

1. Ответ: 23√2.

2. Ответ: 13.

3. Ответ: 6 + 3√6.

4. Ответ: a + √b (при b ≥ 0, a + √b ≠ 0).

5. Ответ: А < В.

6. Ответ: прямая у = 1 при х < 1.

Вариант 4

1. Ответ: 12√3.

2. Ответ: 10.

3. Ответ: 10 + 3√10.

4. Ответ: 2x - √y (при у ≥ 0, 2х - √y ≠ 0).

5. Ответ: А > В.

6. Ответ: прямая у = 1 при х > 2.

Решения

Вариант 5

1. Используем формулы квадрата суммы и квадрата разности, выполним действия и получим:

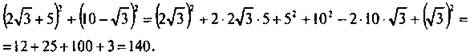
Ответ: 140.

2. Разложим числители дробей на множители и сократим дроби. Имеем:

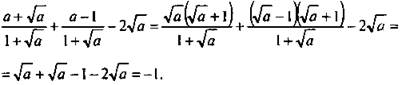
Ответ: -1.

3. Извлечем квадратные корни из выражений и раскроем модули.

Получаем: Было учтено, что √13 ≈ 3,6.

Ответ: 9.

4. Учитывая свойство арифметического квадратного корня, запишем функцию в виде Для построения графика функции у = |х - 2| + х раскроем знак модуля.

а) При х < 2 величина х - 2 < 0 и |х - 2| = -(х - 2) = 2 - х. Поэтому функция имеет вид у = 2 - х + х или у = 2. Строим эту функцию для х < 2.

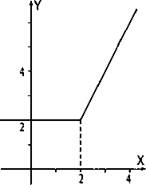
б) При x ≥ 2 величина х - 2 ≥ 0 и |х - 2| = х - 2. Тогда функция имеет вид у = х - 2 + х = 2х - 2. Строим эту функцию для х ≥ 2.

Ответ: см. график.

5. Очевидно, что выражения А и В являются положительными. Рассмотрим квадраты этих величин и Теперь сравним числа 2√6 и 5. Так как 6 < 6,25, то Поэтому А2 < В2 и А < В.

Ответ: А < В.

6. Умножим обе части равенства на сопряженную величину и получим: или или откуда

Ответ: 5.

Вариант 6

1. Используем формулы квадрата суммы и квадрата разности, выполним действия и получим:

Ответ: 60.

2. Разложим числители дробей на множители и сократим дроби. Имеем:

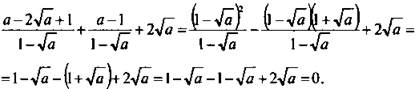
Ответ: 0.

3. Извлечем квадратные корни из выражений и раскроем модули. Получаем: Было учтено, что √11 ≈ 3,3.

Ответ: 13.

4. Учитывая свойство арифметического квадратного корня, запишем функцию в виде Для построения графика функции у = |х - 2| - х раскроем знак модуля.

а) При х < 2 величина х - 2 < 0 и |x - 2| = -(х - 2)= 2 - х. Поэтому функция имеет вид у = 2 – х - х или у = 2 - 2х. Строим эту функцию для х < 2.

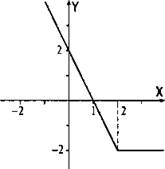
б) При х ≥ 2 величина х - 2 ≥ 0 и |х - 2| = х – 2. Тогда функция имеет вид у = х - 2 - х или у = -2. Строим график функции у = -2 для х ≥ 2.

Ответ: см. график.

5. Очевидно, что выражения А и В являются положительными. Рассмотрим квадраты этих величин и B2 = 13 = 7 + 6. Теперь сравним числа 2√10 и 6. Так как 10 > 9, то √10 > 3 и 2√10 > 6. Поэтому А2 > В2 и А > В.

Ответ: А > В.

6. Умножим обе части равенства на сопряженную величину и получим: или или откуда

Ответ: 3.