Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Подготовка к зачету по теме «Квадратные уравнения» - ДРОБНЫЕ РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ - КВАДРАТНЫЕ УРАВНЕНИЯ
Цель: решение задач по теме «Квадратное уравнение и его корни».
Ход урока
I. Сообщение темы и цели урока
II. Основные понятия (повторение материала)
При необходимости напомните учащимся основные понятия темы. Квадратным уравнением называют уравнение вида ах2 + bх + с = 0, где х — переменная (неизвестная), а, b, с — некоторые числа (а ≠ 0): а — первый коэффициент, b — второй коэффициент, с — свободный член уравнения.
Неполным квадратным уравнением называют уравнение, в котором хотя бы один из коэффициентов Ь или с равен нулю.
Решение неполного квадратного уравнения основано на разложении его левой части на множители.
Если b = 0, то уравнение имеет вид ах2 + с = 0 (при с ≠ 0). При –c/a > 0 уравнение имеет два корня 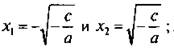 при –c/a < 0 уравнение корней не имеет.
при –c/a < 0 уравнение корней не имеет.
Если с = 0, то уравнение имеет вид ах2 + bх = 0 (при b ≠ 0). Уравнение имеет два корня х1 = 0 и х2 = -b/a.
Если b = 0 и с = 0, то уравнение имеет вид ах2 = 0. Уравнение имеет единственный корень х = 0.
Квадратное уравнение ах2 + bх + с = 0 решается способом выделения квадрата двучлена.
Выражение D = b2 - 4ac называют дискриминантом квадратного уравнения ax2 + bx + c = 0. Если D > 0, то уравнение имеет два корня ![]() (или
(или ![]() ).
).
Если D = 0, то уравнение имеет единственный корень х = -b/2a.
Если D < 0, то уравнение корней не имеет.
Выражение D1 = k2 - ac называют дискриминантом квадратного уравнения ах2 + 2kх + с = 0 (уравнение со вторым четным коэффициентом). Если D1 > 0, то уравнение имеет два корня ![]() Если D1 = 0, то уравнение имеет единственный корень х = -k/a. Если D1 < 0, то уравнение корней не имеет.
Если D1 = 0, то уравнение имеет единственный корень х = -k/a. Если D1 < 0, то уравнение корней не имеет.
Теорема Виета
Если приведенное квадратное уравнение х2 + рх + q = 0 имеет корни х1 и х2, то их сумма х1 + х2 = -р и произведение х1х2 = q.
Если квадратное уравнение ах2 + bх + с = 0 имеет корни х1 и х2, то их сумма х1 + х2 = -b/a и произведение х1х2 = c/a.
Обратная теорема Виета
Если числа m и n такие, что их сумма равна -р, а произведение равно q, то числа m и n являются корнями приведенного квадратного уравнения x2 + px + q = 0.
Уравнение, обе части которого являются рациональными выражениями, называют рациональным. Рациональное уравнение, в котором обе части являются целыми выражениями, называют целым. Рациональное уравнение, в котором хотя бы одна часть является дробным выражением, называют дробным.
Решение дробных рациональных уравнений:
1. Находят общий знаменатель дробей, входящих в уравнение.
2. Умножают обе части уравнения на этот общий знаменатель.
3. Решают получившееся целое уравнение.
4. Исключают те корни, при которых обращается в нуль общий знаменатель дробей.
5. Записывают ответ.
III. Задание на уроке
№ 633 (б); 636 (а); 640 (а); 646; 655; 673 (а, з); 678 (б); 681; 684; 701.
IV. Задание на дом
№ 633 (а, в); 636 (а); 640 (б); 647; 654; 673 (г, ж); 678 (а); 682; 686; 706.
V. Подведение итогов урока