Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Сложение и умножение числовых неравенств - ЧИСЛОВЫЕ НЕРАВЕНСТВА И ИХ СВОЙСТВА - НЕРАВЕНСТВА
Цель: рассмотреть другие свойства числовых неравенств и их применение к решению задач.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (письменный опрос).
Вариант 1
1. Докажите теорему 1.
2. Сформулируйте теорему 3.
3. Оцените величину 5а - 2, если 1,1 < а ≤ 1,2.
4. Сравните числа а и b, если верно неравенство 3а - 3b ≥ 1.
Вариант 2
1. Докажите теорему 2.
2. Сформулируйте теорему 4.
3. Оцените величину 6а - 4, если 1,6 ≤ а < 1,2.
4. Сравните числа а и b, если верно неравенство 4a – 4b ≤ -1.
III. Изучение нового материала (основные понятия)
Рассмотрим другие свойства числовых неравенств — теоремы о почленном сложении и умножении неравенств.
Теорема 5. Если a < b и с < d, то a + c < b + d.
К обеим частям неравенства a < b прибавим число с и получим верное неравенство a + c < b + c. Аналогично, к обеим частям неравенства с < d прибавим число b и получим верное неравенство b + c < b + d. Сравнивая два неравенства a + c < b + c и b + c < b + d, получаем неравенство a + с < b + d. Геометрическая иллюстрация теоремы приведена на рисунке.
![]()
Доказанная теорема справедлива и в случае почленного сложения трех и более неравенств.
Итак, если сложить почленно верные неравенства одного знака, то получится верное неравенство того же знака.
Теорема 6. Если а, b, c, d - положительные числа и а < b, с < d, то ac < bd.
Умножим обе части неравенства а < b на положительное число с и получим верное неравенство ас < bс. Аналогично, умножим обе части неравенства с < d на положительное число b и получим верное неравенство bc < bd. Сравнивая два неравенства ас < bс и bb < bd, получаем неравенство ас < bd. Геометрическая иллюстрация приведена на рисунке.
![]()
Теорема справедлива и в случае почленного умножения трех и более неравенств подобного вида.
Итак, если перемножить почленно верные неравенства одного знака с положительными частями, то получится верное неравенство того же знака.
Обратите внимание учащихся на точную формулировку теоремы. Если среди чисел a, b, с и d имеются отрицательные, то неравенство ас < bd может оказаться и неверным.
Пример 1
Рассмотрим неравенства:
а) -1 < 4 и 2 < 3. При почленном умножении этих неравенств получаем верное неравенство: -1 · 2 < 4 · 3 или -2 < 12.
б) -5 < 1 и -2 < 3. При почленном умножении этих неравенств получаем неверное неравенство: (-5) · (-2) < 1 · 3 или 10 < 3.
Таким образом, при нарушении условий теоремы может быть получено как верное, так и неверное неравенство.
Следствие: если а и b положительные числа и а < b, то аn < bn (n — натуральное число).
Умножим почленно n верных неравенств а < b с положительными левой и правой частями. Тогда получим верное неравенство аn < bn (по теореме 6).
Доказанные свойства неравенств могут быть использованы при оценке суммы, разности, произведения и частного.
Пример 2
Пусть 33 < a < 34 и 2 < b < 3. Оценим сумму, разность, произведение и частное чисел а и b.
а) Почленно сложим два данных двойных неравенства одного знака и получим верное неравенство того же знака: 33 + 2 < a + b < 34 + 3 или 35 < a + b < 37.
б) Для оценки разности a - b сначала оценим число -b. Для этого умножим все части неравенства 2 < b < 3 на отрицательное число -1. Знак неравенства при этом изменится на противоположный: 2 · (-1) > b · (-1) > 3 · (-1) или -2 > -b > -3, т. е. -3 < -b < -2. Теперь почленно сложим два неравенства одного знака 33 < a < 34 и -3 < -b < -2. Получим верное неравенство того же знака: 33 - 3 < а – b < 34 - 2 или 30 < a - b < 32.
в) Почленно умножим два неравенства одного знака 33 < a< 34 и 2 < b < 3 с положительными частями. Получим верное неравенство того же знака: 33 · 2 < a · b < 34 · 3 или 66 < ab < 102.
г) Для оценки отношения a/b сначала оценим число 1/b. Так как в неравенстве 2 < b < 3 все части положительны, то верно неравенство: 1/2 > 1/b > 1/3, т. е. 1/3 < 1/b < 1/2. Теперь почленно умножим два неравенства одного знака 33 < a < 34 и 1/3 < 1/b < 1/2 с положительными частями. Получим верное неравенство того же знака: 33 · 1/3 < a · 1/b < 34 · 1/2 или 11 < a/b < 17.
Рассмотренные свойства неравенств используются и при доказательстве неравенств.
Пример 3
Докажем неравенство ![]()
Для чисел a2 и b2 запишем неравенство между средним арифметическим и средним геометрическим: ![]() (очевидно, что для любого числах верно неравенство |х| ≥ х). Было получено верное неравенство
(очевидно, что для любого числах верно неравенство |х| ≥ х). Было получено верное неравенство ![]() Аналогично запишем еще два неравенства
Аналогично запишем еще два неравенства ![]() Теперь почленно сложим три неравенства одного знака и получим верное неравенство того же знака:
Теперь почленно сложим три неравенства одного знака и получим верное неравенство того же знака: ![]() или
или ![]() Заметим, что неравенство обращается в равенство только при а = b = с (именно в этом случае каждое из неравенств между средним арифметическим и средним геометрическим обращается в равенство).
Заметим, что неравенство обращается в равенство только при а = b = с (именно в этом случае каждое из неравенств между средним арифметическим и средним геометрическим обращается в равенство).
IV. Контрольные вопросы
1. Сформулируйте и докажите теорему 5.
2. Сформулируйте и докажите теорему 6 и следствие из нее.
V. Задание на уроке
№ 747 (б); 749; 750; 752; 754; 756.
VI. Задание на дом
№ 747 (а); 748 (а); 751; 753; 755; 757.
VII. Творческие задания
1. Докажите неравенства (используя неравенство между средним арифметическим и средним геометрическим):
![]()
![]() (а, b — числа одного знака);
(а, b — числа одного знака);
![]() (a, b — числа одного знака);
(a, b — числа одного знака);
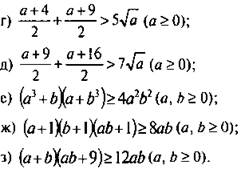
2. Найдите:
а) наименьшее значение выражения х + у, если ху = 16 и х > 0;
б) наименьшее значение выражения 3x + у, если ху = 12 и у > 0;
в) наибольшее значение выражения ху, если х + y = 8 и х, y > 0;
г) наибольшее значение выражения ху, если 3х + у = 30 и х, у > 0.
Ответы: а) 8; б) 12; в) 16; г) 15.
3. Найдите наименьшее значение выражения:
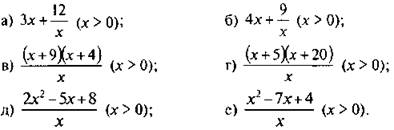
Ответы и указания: а) 12; б) 12;
в) 25, записать выражение в виде ![]()
г) 45, записать выражение в виде ![]()
д) 3, записать выражение в виде ![]()
е) -3, записать выражение в виде ![]()
4. Найдите наибольшее значение выражения.
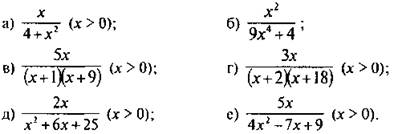
Ответы: ![]() Указание: рассмотрите выражение, обратное данному, и найдите его наименьшее значение (аналогично заданию 3).
Указание: рассмотрите выражение, обратное данному, и найдите его наименьшее значение (аналогично заданию 3).
VIII. Подведение итогов урока