Числовые промежутки - НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ - НЕРАВЕНСТВА

Цель: рассмотреть изображение и запись числовых промежутков.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Докажите теорему 5.

2. Оцените величину 3а – 4b, если 5 < a < 6 и 2 < b < 3.

3. Найдите наименьшее значение выражения

Вариант 2

1. Докажите теорему 6.

2. Оцените величину 5а – 2b, если 7 < a < 8 и 3 < b < 4.

3. Найдите наименьшее значение выражения

III. Изучение нового материала (основные понятия)

Известно, что каждое число х на координатной прямой изображается точкой. Также верно и обратное утверждение: каждая точка на координатной прямой соответствует какому-то числу х. Рассмотрим на координатной прямой точки с координатами -5 и 4. Если точка расположена между ними, то ей соответствует число х, которое больше числа -5 и меньше числа 4 (т. е. число х удовлетворяет двойному неравенству -5 < х < 4).

Верно и обратное утверждение: если число х удовлетворяет неравенству -5 < х < 4, то на координатной оси число х изображается точкой, расположенной между точками с координатами -5 и 4. Множество всех чисел, удовлетворяющих условию -5 < х < 4, называют числовым промежутком (или промежутком) от -5 до 4 и обозначают символом (-5; 4) (при этом читают «промежуток от -5 до 4»). Такой промежуток изображен (заштрихован) на рисунке. Заметим, что круглые скобки в символе (-5; 4) указывают, что границы -5 и 4 в рассматриваемый промежуток не входят.

В математике рассматриваются и другие виды промежутков. В таблице для каждого вида числового промежутка приведены его изображение на координатной оси, запись с помощью неравенств, обозначение и прочтение.

Геометрическое изображение	Запись с помощью неравенств	Обозначение	Прочтение
	-5 < х < 4	(-5; 4)	Промежуток от -5 до 4
	-5 ≤ x ≤ 4	[-5; 4]	Промежуток от -5 до 4, включая -5 и 4
	-5 ≤ х < 4	[-5; 4)	Промежуток от -5 до 4, включая -5
	-5 < х ≤ 4	(-5; 4]	Промежуток от -5 до 4, включая 4
	х > 4	(4; +∞)	Промежуток от 4 до плюс бесконечности
	Х ≥ 4	[4; +∞)	Промежуток от 4 до плюс бесконечности, включая 4
	х < -5	(-∞; -5)	Промежуток от минус бесконечности до -5
	X ≤ 5	(-∞; -5]	Промежуток от минус бесконечности до -5, включая -5

Заметим, что если граничная точка в промежуток не входит, то на координатной оси она изображается пустой точкой и в обозначении промежутка выделяется круглой скобкой. Если граничная точка в промежуток входит, то на координатной оси она изображается заполненной точкой и в обозначении промежутка выделяется квадратной скобкой.

Множество действительных чисел изображается всей координатной прямой. Это множество обозначают (-∞; +∞) (читается «промежуток от минус бесконечности до плюс бесконечности»).

Для дальнейшего обсуждения темы рассмотрим некоторые понятия теории множеств. Множество относится к первичным неопределяемым понятиям (подобно понятию натурального числа, точки, плоскости и т. д.). Поэтому под множеством будем понимать совокупность (или набор) элементов, отобранных по определенному признаку (признакам). Например: множество книг в шкафу, множество точек данной фигуры, множество двузначных натуральных чисел и т. д. Заметим, что понятие «множество» не следует понимать как совокупность, содержащую «много» элементов. Множество может содержать один, два и т. д. элемента. Более того, в математике приходится рассматривать и пустое множество, которое не содержит ни одного элемента. Например, множество книг в данном шкафу (а шкаф может быть и одежным) может оказаться пустым.

Множества обычно обозначают прописными буквами латинского алфавита: А, В и т. д., а их элементы — строчными буквами: а, b,... Пустое множество обозначают символом Ø. Если множество А состоит из n элементов a1, a2 ..., an, то пишут A = { a1, a2 ..., an}.

Говорят, что «элемент а принадлежит множеству А» и записывают а ∈ А или А ∋ а (А содержит а). «Элемента а не принадлежит множеству А» (А не содержит а) записывают так: а ∉ А или

Пример 1

Пусть A — множество цифр, т. е. A = {0,1,2,...,9}. Тогда, очевидно, 7 ∈ А и 10 ∉ А.

Рассмотрим две основные операции над множествами: пересечение множеств и объединение множеств.

Пересечением множеств А и В называют множество, состоящее из всех элементов, принадлежащим одновременно обоим множествам. Пересечение этих множеств обозначают символом А∩В.

Пример 2

Пусть даны множества А = {2,3,5,7,9} и B = {1,3,7,8,9}. Так как числа 3, 7 и 9 одновременно принадлежат обоим множествам, то эти числа являются элементами множества А∩В ,т. е. A∩В = {3,7,9}.

Можно дать наглядную иллюстрацию такой операции. Пусть А и В — множества точек данных фигур. Тогда фигура, являющаяся общей частью фигур А и В, содержит точки, одновременно принадлежащие этим фигурам. Поэтому эта общая часть — пересечение данных множеств А∩В (выделено двойной штриховкой).

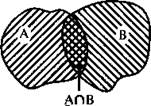
Если множества А и В не имеют общих элементов, то пересечением этих множеств будет пустое множество.

Объединением множеств A и В называют множество, состоящее из всех элементов, принадлежащих хотя бы одному из этих множеств. Объединение этих множеств обозначают символом AUВ.

Пример 3

Еще раз вернемся к примеру 2. Опять рассмотрим множества A = {2,3,5,7,9} и В = {1,3,7,8,9}. Так как числа 1, 2, 3, 5, 7, 8, 9 принадлежат или множеству А, или множеству В, или обоим этим множествам, то эти числа являются элементами множества АUВ, т. е. AUB = {1,2,3,5,7,8,9}.

Дадим иллюстрацию такой операции. Заштрихованная фигура содержит точки, принадлежащие или фигуре А, или фигуре В, или обеим этим фигурам. Поэтому заштрихованная фигура — объединение данных множеств А и В.

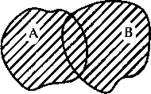
Теперь рассмотрим множества, представляющие собой числовые промежутки.

Пример 4

а) На рисунке изображены промежутки [-2; 3) и (1; 5]. Промежуток (1; 3) представляет собой их общую часть.

Поэтому промежуток (1; 3) является пересечением промежутков [-2; 3)]. Это можно записать так: [-2; 3)∩(1; 5] = (1; 3). Промежуток [-2; 5] является объединением промежутков [-2; 3) и (1; 5], т. к. любая точка промежутка [-2; 5] принадлежит или промежутку [-2; 3), или промежутку (1; 5], или обоим промежуткам одновременно. Это можно записать так: [-2; 3)U(1; 5] = [-2; 5].

б) На рисунке изображены промежутки [-2; 1) и (3; 5]. Эти промежутки не имеют общих точек. Поэтому пересечением этих промежутков является пустое множество, т. е. [-2; 1)∩(3; 5] = Ø. Объединением этих промежутков (-2; 1)U(3; 5] являются сами эти промежутки (а не один промежуток), т. к. любая точка из множества [-2; 1)U(3; 5] принадлежит или промежутку [-2; 1), или промежутку (3; 5].

IV. Контрольные вопросы

1. Приведите примеры разных видов числовых промежутков.

2. Дайте определение пересечения и объединения множеств А и В.

3. Рассмотрите два промежутка. Укажите их пересечение и объединение. Ответ обоснуйте.

V. Задание на уроке

№ 761 (а, д, ж); 763 (а, г); 764 (в, г); 765 (а); 768; 770 (а, б); 771 (а); 772; 774 (б, в).

VI. Задание на дом

№ 762; 763 (б, в); 764 (а, б); 765 (б); 767; 770 (в, г); 771 (в); 773 (а, г); 775 (а, г).

VII. Творческие задания

1. Найдите пересечение и объединение множеств А и В:

а) А = {1,5,6,7,10,12,14}, В = {2,3,5,8,9,11,12}.

б) А = {А,Б,Г,Д,Е,Ж,К}, В = {Б,В,Е,К,Л,М}.

в) А = {Оля,Петя,Юра,Лена,Вова}, В = {Катя,Петя,Витя,Лена,Миша].

г) А — множество натуральных двузначных чисел, В — множество чисел, кратных 5.

д) А — множество отрицательных целых чисел, В — множество цифр.

2. Найдите пересечение и объединение множеств А, В и С.

а) А = {1,3,5,6,8.11}, В = {2,5,7,11,12}, C = {1,5,6,9,11}.

б) А: (-3; 5) B: [-4; 4) С: (-2; 4].

VIII. Подведение итогов урока