Зачетная работа по теме «Неравенства» - НЕРАВЕНСТВА С ОДНОЙ ПЕРЕМЕННОЙ И ИХ СИСТЕМЫ - НЕРАВЕНСТВА

Цель: проверка знаний учащихся по вариантам одинаковой сложности.

Ход урока

I. Сообщение темы и цели урока

II. Характеристика зачетной работы

По сравнению с контрольной работой в зачетной увеличено количество заданий. Соответственно у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи находятся в части А, более сложные — в части В, еще сложнее — в части С. Каждая задача из А оценивается в 1 балл, из В — в 2 балла, из С — в 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка «3» ставится за 6 баллов, оценка «4» — за 10 баллов, оценка «5» — за 14 баллов.

Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного занятия можно и не посвящать (решения задач могут быть вывешены на стенде).

III. Задания зачетной работы

ЗР-4

А

Решите неравенство:

3. Решите систему неравенств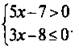

4. При каких значениях х функция у = 3х + 5 принимает отрицательные значения?

5. Найдите целые решения неравенства -2 ≤ 3х + 1 < 7.

6. Длины сторон прямоугольника (в см) удовлетворяют условию 1,2 < a < 1,3 и 2,7 < b < 2,8. Оцените периметр прямоугольника.

7. При каких значениях а уравнение 3х + 2 = с имеет положительный корень?

В

8. Сравните числа А = 234 · 236 и В = 2352.

9. Решите неравенство |2 - 3х| ≤ 7.

10. Найдите область определения функции

11. Решите неравенство

С

12. Решите неравенство

13. Докажите неравенство

14. В раствор объемом 8 л, содержащий 60% кислоты, вливают раствор, содержащий 20% кислоты. Сколько нужно влить второго раствора в первый, чтобы смесь содержала кислоты не меньше 30% и не больше 40%?

IV. Разбор заданий зачетной работы

1. Умножим обе части неравенства на положительное число 2 (при этом знак неравенства сохраняется) и получаем: 6х + х ≤ 28 или 7х ≤ 28. Разделим обе части неравенства на положительное число 7 (знак неравенства сохраняется) и получим х ≤ 4, т. е. х ∈ (-∞; 4].

Ответ: (-∞; 4].

2. В неравенстве раскроем скобки и приведем подобные члены. Получаем: или 5х > -2. Разделим обе части на положительное число 5 (знак неравенства сохраняется) и найдем х > -0,4, т. е. х ∈ (-0,4; +∞).

Ответ: (-0,4; +∞).

3. В системе неравенств решим каждое неравенство: и 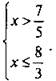Получаем решение данной системы неравенств т. е. х ∈ (7/5; 8/3].

Ответ: (7/5; 8/3].

4. Если функция у = 3х + 5 принимает отрицательные значения, то выполняется неравенство: 3х + 5 < 0 или 3х < -5. Решение этого неравенства х < -5/3, т. е. х ∈ (-∞; -5/3).

Ответ: (-∞; -5/3).

5. Сначала решим двойное неравенство -2 ≤ 3x + 1 < 7. Вычтем из всех частей неравенства число 1 и получим -3 ≤ 3х < 6. Разделим все части неравенства на положительное число 3 (при этом знаки неравенства сохраняются) и найдем -1 ≤ x < 2, т. е. х ∈ [-1; 2). Выпишем все целые числа, входящие в этот промежуток: -1; 0; 1.

Ответ: -1; 0; 1.

6. Периметр прямоугольника равен P = 2(a + b). Оценим сначала сумму a + b. Для этого почленно сложим неравенства одного знака 1,2 < a < 1,3 и 2,7 < b < 2,8 и получим 3,9 < a + b < 4,1. Умножим все части этого неравенства на положительное число 2 (знаки неравенства сохраняются) и найдем: 7,8 < 2(а + b) < 8,2 или Р ∈ (7,8; 8,2).

Ответ: (7,8; 8,2).

7. Сначала решим уравнение 3х + 2 = а. Получаем 3х = a - 2, откуда Так как этот корень положительный, то получаем неравенство: или а - 2 > 0, откуда а > 2, т. е. а ∈ (2; +∞).

Ответ: (2; +∞).

8. Запишем число А в виде Тогда видно, что число А меньше числа В = 2352. Итак, А < В.

Ответ: А < В.

9. Неравенство |2 - 3х| ≤ 7 равносильно двойному неравенству -7 ≤ 2 – 3x ≤ 7. Вычтем из всех частей неравенства число 2 и получим -9 ≤ -3x ≤ 5. Разделим все части неравенства на отрицательное число -3. При этом знаки неравенства меняются на противоположные. Получим 3 ≥ x ≥ -5/3, т. е. х ∈ [-5/3; 3].

Ответ: [-5/3; 3].

10. Область определения данной функции задается условиями: подкоренные выражения неотрицательны, и делить на нуль нельзя. Поэтому получаем систему неравенств Решим каждое неравенство системы 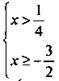и найдем решение системы х > 1/4, т. е. х ∈ (1/4; +∞).

Ответ: (1/4; +∞).

11. В неравенстве множитель 5x2 + 7 положительный при всех значениях х. Поэтому разделим обе части данного неравенства на этот множитель (при этом знак неравенства сохраняется) и получаем равносильное неравенство 3х + 2 ≥ 0. Решение этого неравенства х ≥ -2/3, т. е. x ∈ [-2/3; +∞).

Ответ: [-2/3; +∞).

12. В неравенстве очевидно, знаменатель положительный, т. е. х - 2 > 0 или х > 2. Умножим обе части данного неравенства на положительную величину х - 2. При этом знак неравенства сохраняется. Получаем: 8 > 2(х - 2) или 4 > х - 2, откуда 6 > х. Таким образом 2 < х < 6 или х ∈ (2; 6).

Ответ: (2; 6).

13. Для доказательства неравенства раскроем скобки, перенесем все члены в левую часть и выделим полные квадраты по переменным а и b. Получаем: или или Так как левая часть неравенства является суммой квадратов двух величин а - 2 и 2b + 1 , то при всех а и b такое неравенство выполняется.

Ответ: доказано.

14. В растворе объемом 8 л, содержащем 60% кислоты, л чистой кислоты. Пусть добавили х (л) раствора, содержащего 20% кислоты. Тогда в этом растворе находится (л) чистой кислоты. Посчитаем процентное содержание кислоты в смеси.

Количество чистой кислоты в смеси равно 4,8 + 0,2х (л). Объем смеси равен 8 + х (л). Тогда процентное содержание кислоты в смеси По условию 30 ≤ Р ≤ 40. Получаем систему неравенств 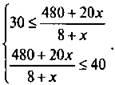Так как величина 8 + х > 0, то умножим каждое неравенство на эту величину. При этом знак неравенства сохраняется. Получаем систему линейных неравенств: или или откуда 8 ≤ х ≤ 24.

Ответ: [8; 24] л.