Простейшая квадратичная функция у = х1 и ее свойства - ФУНКЦИЯ у = х2 - КВАДРАТИЧНАЯ ФУНКЦИЯ

Цель: рассмотрение функции у = х2, ее свойств, построение графика функции.

Ход урока

I. Сообщение темы и цели урока

II. Повторение и закрепление пройденного материала

1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).

2. Контроль усвоения материала (письменный опрос).

Вариант 1

1. Какая функция называется квадратичной?

2. Найти значение функции y = -3х2 + 7х - 2 при х = -3.

3. При каком значении аргумента функция у = 2х2 - 5х + 1 принимает значение у = -1?

4. Известно, что y(х - 3) = -х2 + 12х - 30. Найти у(х).

Вариант 2

1. Какие значения аргумента называются нулями функции?

2. Найти значение функции y = -2х2 + 5х - 8 при х = -2.

3. При каком значении аргумента функция у = 3х2 - 4х + 2 принимает значение у = 22?

4. Известно, что у(2 - х) = -2х2 + 3х - 2. Найти y(х).

III. Изучение нового материала (основные понятия)

Рассмотрим частный случай квадратичной функции у = ax2 + bх + с при а = 1, b = 0 и с = 0 — функцию у = х2 (простейшая квадратичная функция). Составим таблицу значений этой функции на промежутке х ∈ [-3; 3] с шагом 0,5.

x	-3	-2,5	-2	-1,5	-1	-0,5	0
y	9	6,25	4	2,25	1	0,25	0

x	0,5	1	1,5	2	2,5	3
y	0,25	1	2,25	4	6,25	9

Отметим на координатной плоскости точки, указанные в таблице, и проведем через них плавную кривую. Получим график функции у = х2. Кривая, которая является графиком функции у = х2, называется параболой.

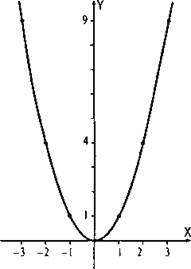
Учитывая построенный график и проведя исследование функции у = х2, рассмотрим ее основные свойства.

1. Область определения функции — все действительные значения х.

2. Область изменения (значений) функции — все неотрицательные значения у, т.е. у ∈ [0; +∞). Очевидно, что при всех значениях х величина у = х2 ≥ 0.

3. Значения функции у > 0 при x ≠ 0 и у = 0 при х = 0. Поэтому парабола проходит через начало координат, все остальные точки ее лежат выше оси абсцисс. Говорят, что парабола у = х2 касается оси абсцисс в точке (0; 0).

4. Функция у = х2 является четной, т. е. выполнено равенство у(-х) = у(х) (или (-х)2 = х2). Например, у(-2) = у(2) = 4. Поэтому график этой функции симметричен относительно оси ординат (или ось ординат является осью симметрии параболы). Точку пересечения параболы с ее осью симметрии называют вершиной параболы. Для параболы у = х2 вершиной является начало координат, т. е. точка (0; 0).

5. Функция у = х2 возрастает на промежутке х ≥ 0 и убывает на промежутке х ≤ 0.

Напомним, что функция у = х2 называется возрастающей, если большему значению аргумента x соответствует большее значение функции у (т. е. если x1 > х2, то и у(х1) > у(х2)).

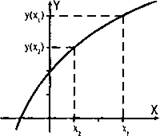
Как видно из рисунка, для значения аргумента х1 значение функции у(х1) больше, чем аргумента х2.

Функция у(х) называется убывающей, если большему значению аргумента х соответствует меньшее значение функции у (т. е. если х1 > x2, то y(х1) < у(х2)).

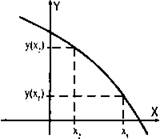
Из рисунка видно, что для значения аргумента x1 значение функции y(x1) меньше, чем для аргумента х2.

Пример 1

Докажем, что функция у(х) = х2 возрастает на промежутке х ≥ 0 и убывает на промежутке х ≤ 0.

Возьмем два произвольных значения аргумента x1 и х2, пусть x1 > х2. Тогда соответствующие значения функции Найдем разность у(х1) - y(х2) и определим ее знак: В этом выражении х1 - х2 > 0, т. к. х1 > х2. Множитель х1 + х2 может иметь разный знак. Рассмотрим два случая.

а) На промежутке х ≥ 0, очевидно, х1 > 0 и х2 ≥ 0. Поэтому сумма х1 + х2 > 0. Тогда величина y(x1) - y(x2) представляет собой произведение двух положительных множителей х1 - х2 и х1 + х2 и также положительна, т. е. y(x1) - y(x2) > 0 или у(х1) > у(х2). Мы показали, что на промежутке х ≥ 0 большему значению аргумента х1 соответствует большее значение функции y(x1). Тогда (но определению) на таком промежутке функция у(х) возрастает.

б) На промежутке х ≥ 0, очевидно, х1 ≤ 0 и х2 < 0. Поэтому сумма х1 + х2 < 0. Тогда множитель х1 - х2 > 0, а множитель х1 + х2 < 0. Произведение таких множителей отрицательно, т. е. у(х1) - y(х2) < 0 или y(х1) < y(x2). Было показано, что на промежутке х ≤ 0 большему значению аргумента х, соответствует меньшее значение функции y(х1). Тогда (по определению) на таком промежутке функция у(х) убывает.

Пример 2

Найдем координаты точек пересечения параболы у = х2 и прямой у = х + 2.

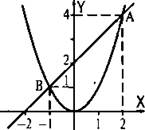
Координаты точек пересечения параболы у = х2 и прямой у = х + 2 являются решением системы уравнений Приравняв правые части уравнений, получим квадратное уравнение: х2 = х + 2 или х2 - х - 2 = 0. Корни этого уравнения x1 = -1 и х2 = 2. Найдем соответствующие значения функции у(-1) = (-1)2 = 1 и у(2) = 22 = 4. Таким образом, данные парабола и прямая пересекаются в двух точках А(2; 4) и В(-1; 1).

Пример 3

Построим график функции

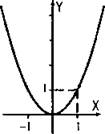
Учтем, что х - 1 ≠ 0 (т. е. х ≠ 1) и сократим дробь: Теперь построим график функции у = х2 (параболу) и удалим из нее точку, для которой х = 1 (показана стрелками).

Пример 4

Построим график функции

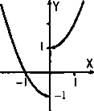
Учтем, что х ≠ 0. Раскроем знак модуля, рассмотрев два случая:

а) при х > 0 имеем |х| = х и функция у = х2 + 1. Построим этот график для положительных х (он получается смещением ветви параболы на одну единицу вверх) — часть 1 графика.

б) при х < 0, очевидно |х| = -х и функция у = х2 – 1. Строим этот график для отрицательных значений х. Он получается смещением ветви параболы на одну единицу вниз. Получаем часть графика 2. Стрелки указывают, что при х = 0 данная функция не существует.

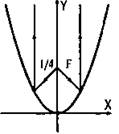
Разумеется, функция у = х2 имеет и другие (более сложные) свойства, которые находят применение в технике. Например, на оси симметрии параболы имеется точка, называемая фокусом параболы. Если в этой точке находится источник света, то все отраженные от параболы лучи идут параллельно оси симметрии параболы. Такое свойство используют при изготовлении прожекторов, телескопов, локаторов, дальномеров и т. д.

Фокусом параболы у = х2 является точка F(0; 1/4).

IV. Контрольный вопросы

1. Какая кривая называется параболой?

2. Перечислите основные свойства функции у = х2.

3. Какая функция называется: а) возрастающей, б) убывающей?

4. Каким свойством обладает фокус параболы?

V. Задание на уроке

№ 587; 589 (3, 4); 590 (5); 592 (1,4); 594 (1, 2).

VI. Задание на дом

№ 586 (1); 588; 589 (1, 2); 590 (6); 592 (2, 3); 593; 594 (3, 4).

VII. Творческие задания

1. Построить график функции:

Ответы: a) у = х2, х ≠ ±1; б) у = х2; в) у = х2, х ≠ 3; г) у = х2, х ≠ ±2.

2. Построить график функции:

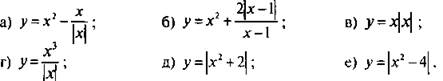
Ответы: а) у = х2 + 1 при х < 0, у = х2 - 1 при х > 0;

б) у = х2 - 2 при х < 1, у = х2 + 2 при х> 1;

в) у = -х2 при х < 0, у = х2 при х ≥ 0;

г) у = -х2 при х < 0, у = х2 при х > 0;

д) у = х2 + 2;

с) у = х2 - 4 при х < -2 и при х > 2, у = 4 - х2 при -2 ≤ х ≤ 2.

VIII. Подведение итогов урока