Зачетная работа по теме «Квадратичная функция» - ПОСТРОЕНИЕ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ - КВАДРАТИЧНАЯ ФУНКЦИЯ

Цель: проверка знаний учащихся по вариантам одинаковой сложности.

Ход урока

I. Сообщение темы и цели урока

II. Характеристика зачетной работы

По сравнению с контрольной работой в зачетной увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи находятся в части А, более сложные — в части В, еще сложнее — в части С. Каждая задача из А оценивается в 1 балл, из В — в 2 балла, из С — в 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка «3» ставится за 6 баллов, оценка «4» — за 10 баллов, оценка «5» — за 14 баллов.

Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного занятия можно и не посвящать (решения задач могут быть вывешены на стенде). Для стендового размещения разбор заданий приводится.

III. Задания зачетной работы

А

1. Дана функция у(х) = -7х2 + 3х - 4. Найти y(-2).

2. При каких значениях аргумента значение функции у = 2х2 - 7х + 9 равно 4?

3. Найдите координаты вершины параболы у = 3х2 + 4х + 1.

4. Напишите уравнение параболы у = х2 + px + q, проходящей через точки А(-2; 19) и В(3; -11).

5. Найти общие точки параболы y = 3х2 – 5x + 3 и прямой у = 2х - 1.

6. Периметр прямоугольника равен 60 см. Какими должны быть его стороны, чтобы площадь прямоугольника была наибольшей? Найти эту площадь.

7. Постройте фафик функции у = -х2 - 2х + 3 .

В

8. Дана функция у(х) = 3х2 - 2х + 1. Найти у(2х - 1).

9. Написать уравнение параболы, проходящей через точки А(-1; 1), В(0; -4) и С(2; -2).

10. Функция у = 3х2 + bx - 4 принимает наименьшее значение в точке х0 = -2. Найдите это значение.

11. Постройте график функции у = х2 - 4|х| + 3.

С

12. Дана функция у(2 - х) = 2х2 – х - 5. Найти у(х).

13. При каких значениях параметра k прямая у = (k - 3)х - 15 касается параболы у = 3х2 – 2kх – 3? Найти эти точки.

14. Постройте график функции у = |x2 – 4x|.

IV. Разбор заданий зачетной работы

1. Подставим значение аргумента х = -2 в уравнение функции и получим

Ответ: -38.

2. Так как значение функции равно 4, то получим квадратное уравнение 2x2 – 7x + 9 = 4 или 2х2 - 7х + 5 = 0. Его корни х1 = 1 и х2 = 2,5.

Ответ: x1 = 1 и х2 = 2,5.

3. Для квадратичной функции у = 3х2 + 4х + 1 найдем координаты вершины параболы: и

Ответ: x0 = -2/3, y0 = -1/3.

4. Так как парабола у = х2 + px + q проходит через точки А(-2; 19) и В(3; -11), то координаты этих точек удовлетворяют уравнению параболы. Получаем систему уравнений: или Вычтем из первого уравнения второе и получим: 35 = -5р, откуда р = -7. Подставим эту величину в первое уравнение: 15 = -2 · (-7) + q и найдем q = 1. Итак, уравнение параболы у = х2 - 7х + 1.

Ответ: у = х2 - 7х + 1.

5. Координаты общей точки параболы и прямой удовлетворяют системе уравнений Приравняем правые части уравнений и получим квадратное уравнение 3х2 - 5х + 3 = 2х - 1 или 3х2 - 7х + 4 = 0, корни которого х1 = 1 и x2 = 4/3. Используя второе уравнение, найдем соответствующие значения у: у = 2 · 1 - 1 и y2 = 2 · 4/3 - 1 = 5/3. Итак, данные парабола и прямая имеют две общие точки (1; 1) и (4/3; 5/3).

Ответ: (1; 1) и (4/3; 5/3).

6. Полупериметр прямоугольника равен 30 см. Если одна его сторона равна х (см), то другая 30 - х(см). Площадь прямоугольника S = х(30 - х) = -х2 + 30x. Эта функция имеет наибольшее значение при х = 15 и такая площадь равна S = -152 + 30 · 15 = 225 (см2). Итак, при заданном периметре прямоугольника наибольшую площадь 225 см2 имеет квадрат со стороной 15 см.

Ответ: 15 см, 15 см, 225 см.

7. Построим график функции у = -х2 - 2х + 3. Найдем точки пересечения графика с осью абсцисс. Получаем уравнение 0 = -х2 - 2х + 3, корни которого х1 = -3 и х2 = 1. Абсцисса вершины параболы и ордината Найдем точку пересечения с осью ординат. Положим х = 0 и получим у(0) = 3. Через отмеченные точки проведем параболу.

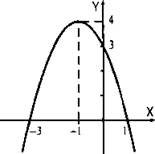
Ответ: см. график.

8. Для функции y(х) = 3х2 - 2х + 1 подставим значение аргумента 2х - 1 и получим

Ответ: 12х2 - 16х + 6.

9. Общее уравнение параболы у = ax2 + bх + с. Так как парабола проходит через точки A(-1; 1), В(0; -4) и С(2; -2), то координаты этих точек удовлетворяют уравнению параболы. Получаем систему линейных уравнений 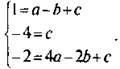Подставим значение с = -4 в первое и третье уравнения и получим систему уравнений или Вычтем из первого уравнения второе и получим 4 = -a, откуда a = -4. Подставим это значение в первое уравнение 5 = -4 - b, откуда b = -9. Тогда уравнение параболы у = -4х2 - 9х - 4.

Ответ: у = -4х2 - 9х - 4.

10. Так как функция у = 3х2 + bх - 4 принимает наименьшее значение в точке х0 = -2, то получаем уравнение откуда b = 12. Поэтому функция имеет вид у(х) = 3х2 + 12х - 4. Найдем наименьшее значение функции

Ответ: -16.

11. Построим график функции у = x2 - 4|x| + 3. Значения функции при двух симметричных значениях аргумента совпадают, например, у(-2) = у(2) = -1. Поэтому график данной функции симметричен относительно оси ординат. Достаточно построить график функции при х ≥ 0 и зеркально отразить его влево относительно оси ординат.

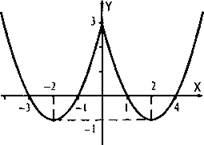
Ответ: см. график.

12. Дана функция у(2 - х) = 2х2 – х - 5. Чтобы найти у(х), введем новую переменную t = 2 - х, выразим х = 2 - t. Подставим эту величину в функцию y(2 - x) = 2x2 – x - 5 и получим Итак, имеем y(t) = 2t2 -7t + 1. Так как не имеет значения, какой буквой обозначен аргумент функции, то можно считать, что у(х) = 2х2 - 7х + 1.

Ответ: у(х) = 2х2 - 7х + 1.

13. Точка касания (х0; y0) данных прямой и параболы является единственным решением системы уравнений Приравняем правые части уравнений и получим квадратное уравнение: или 0 = x2 - (k - 1)x + 4. Это квадратное уравнение (а следовательно, и система уравнений) имеет единственное решение, если дискриминант D = (k - 1)2 - 16 = 0 или (k - 1)2 = 16 , или k - 1 = ±4, откуда k = 1 ± 4, т. е. k1 = -3 и k2 = 5.

а) При k = -3 уравнение 0 = x2 - (k - 1)x + 4 имеет вид: 0 = х2 + 4x + 4 или 0 = (х + 2)2, откуда х = -2. Из первого уравнения системы найдем

б) При k = 5 уравнение 0 = x 2 - (k - 1)x + 4 имеет вид: 0 = х2 - 4х + 4 или 0 = (х - 2)2, откуда х = 2. Из первого уравнения системы найдем у = 2x - 15 = 2 · 2 - 15 = -11.

Итак, при k = -3 точка касания (-2; -3), при k = 5 точка касания (2; -11).

Ответ: При k = -3 (-2; -3), при k = 5 (2; -11).

14. Построим график функции у = |х2 - 4х|. Сначала построим график функции у = х2 - 4х по характерным точкам: точкам пересечения с осями координат и вершине параболы (пунктирная кривая). Для тех частей параболы, для которых значения у ≥ 0 (части АВ и CD) функции у = |х2 - 4х| и у = х2 - 4х совпадают. Поэтому кривые АВ и CD являются также частями графика функции у = |х2 - 4х|.

Для той части графика, для которой значение у < 0 по определению модуля |х2 - 4х| = -(х2 - 4х). Поэтому ординаты части BED графика меняют знак на противоположный. Кривая BED отражается относительно оси абсцисс и переходит в кривую BFD.

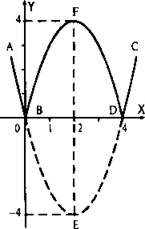
Итак, график функции y = |x2 - 4x| построен.

Ответ: см. график.