Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Понятие о квадратном неравенстве и его решении, аналитический способ решения - КВАДРАТНОЕ НЕРАВЕНСТВО И ЕГО РЕШЕНИЕ - КВАДРАТНЫЕ НЕРАВЕНСТВА
Цель: рассмотрение квадратного неравенства и его решения, аналитического способа решения.
Ход урока
I. Сообщение темы и цели урока
II. Изучение нового материала (основные понятия)
Понятие квадратного неравенства аналогично понятию квадратного уравнения. Если в одной части неравенства стоит квадратный трехчлен, а в другой — число нуль, такое неравенство называют квадратным. Например, неравенства 3х2 - 2х - 1 ≤ 0 и -5х2 + 3х + 2 > 0 являются квадратными. Вообще, если в части неравенства переменная х входит в степени 2 и ниже, то после несложных преобразований такое неравенство сводится к квадратному.
Пример 1
В неравенстве 2х2 ≥ 5х - 3 перенесем (изменяя знак) члены 5х и -3 в левую часть и получим квадратное неравенство 2х2 - 5х + 3 ≥ 0.
Напомним, что решением неравенства с одним неизвестным называется такое значение неизвестного, при котором это неравенство обращается в верное числовое неравенство. Решить неравенство — значит найти все его решения или доказать, что их нет. Например, для неравенства примера 1 число х = 2 является одним из решений, а число х = 1,2 — нет.
К квадратным неравенствам приводят многие геометрические и текстовые задачи.
Пример 2
Одну сторону квадрата увеличили на 2 см, а другую — на 6 см. Площадь получившегося прямоугольника стала больше 45 см3. Какова была сторона квадрата?
Пусть сторона квадрата равна х см, тогда стороны прямоугольника (х + 2) см и (х + 6) см и его площадь равна (х + 2)(х + 6) см2. По условию задачи получаем неравенство (х + 2)(x + 6) > 45 или х2 + 8х + 12 > 45, или x2 + 8x – 33 > 0. Разложим левую часть неравенства на множители (х – 3)(х + 11) > 0. Так как по условию х > 0, то и х + 11 > 0. Разделим обе части неравенства на положительное выражение х + 11, (при этом знак неравенства сохраняется) и получаем линейное неравенство х - 3 > 0, откуда х > 3. Итак, сторона квадрата больше 3 см.
Пример 3
На плану производит построение рота солдат, состоящая не менее чем из 72 человек. Оказалось, что шеренг на 6 больше, чем солдат в каждой шеренге. Сколько может быть солдат в каждой шеренге?
Пусть число солдат в каждой шеренге равно х, тогда число шеренг равно х + 6 и число солдат в роте равно х(х + 6). По условию задачи получаем неравенство х(х + 6) ≥ 72 или х2 + 6х – 72 ≥ 0. Разложим левую часть этого квадратного неравенства на множители (х + 12)(х - 6) ≥ 0. Так как по условию х > 0, то и х + 12 > 0. Разделим обе части неравенства на положительное выражение х + 12 (при этом знак неравенства сохраняется) и получаем линейное неравенство х - 6 ≥ 0, откуда х ≥ 6. Итак, в каждой шеренге находится не менее 6 солдат.
Заметим, что в двух последних примерах по условию задачи возникало дополнительное условие х > 0, что позволило легко свести квадратное неравенство к линейному неравенству и решить его. Теперь рассмотрим решение квадратных неравенств (без ограничений на х).
Пример 4
Решим неравенство x2 + 8х – 33 > 0.
Квадратное уравнение х2 + 8х - 33 = 0 имеет два корня x1 = -11 и х2 = 3. Поэтому квадратный трехчлен x2 + 8x - 33 можно разложить на множители x2 + 8x – 33 = (x + 11)(x - 3). Тогда данное неравенство имеет вид (х + 11)(х - 3) > 0. Произведение двух множителей положительно, если они имеют одинаковые знаки. Рассмотрим два случая.
1) Пусть оба множителя положительны, т. е. х + 11 > 0 и х - 3 > 0. Получаем систему линейных неравенств ![]() Решая систему, имеем
Решая систему, имеем ![]() откуда х > 3. Итак, все числа х > 3 являются решениями неравенства (х + 11)(x - 3) > 0.
откуда х > 3. Итак, все числа х > 3 являются решениями неравенства (х + 11)(x - 3) > 0.
2) Пусть оба множителя отрицательны, т. е. х + 11 < 0 и х – 3 < 0. Получаем систему линейных неравенств ![]() Решая систему, имеем
Решая систему, имеем ![]() откуда х < -11. Итак, все числа х < -11 также являются решениями неравенства (х + 11)(x - 3) > 0. Таким образом, решениями неравенства (х + 11)(x - 3) > 0, а следовательно, и данного неравенства х2 + 8х – 33 > 0 являются числа х < -11 и числа х > 3. Итак, х < -11, х > 3.
откуда х < -11. Итак, все числа х < -11 также являются решениями неравенства (х + 11)(x - 3) > 0. Таким образом, решениями неравенства (х + 11)(x - 3) > 0, а следовательно, и данного неравенства х2 + 8х – 33 > 0 являются числа х < -11 и числа х > 3. Итак, х < -11, х > 3.
Итак, при решении квадратного неравенства ax2 + bx + c > 0 или ax2 + bx + c < 0 надо:
1. Решить квадратное уравнение aх2 + bх + с = 0 и найти корни х1 и х2.
2. Разложить квадратный трехчлен ax2 + bx + c на множители ax2 + bx + c = а(х – х1)(x - х2).
3. Неравенство а(х – х1)(x – х2) > 0 или а(х – х1)(x – х2) < 0 свести к системам линейных неравенств.
4. Решить эти системы неравенств и записать ответ.
Пример 5
Решим неравенство -7х2 + 5х + 2 ≥ 0.
Для удобства запишем неравенство в виде неравенства с положительным первым коэффициентом. Для этого умножим обе части неравенства на отрицательное число -1. При этом знак неравенства меняется на противоположный и получаем 7х2 - 5х – 2 ≤ 0. Найдем корни уравнения 7х2 - 5х - 2 = 0. Имеем ![]() т. е. х1 = 1 и х2 = -2/7. Разложим квадратный трехчлен на множители и получим неравенство
т. е. х1 = 1 и х2 = -2/7. Разложим квадратный трехчлен на множители и получим неравенство ![]() Так как число 7 положительно, то неравенство
Так как число 7 положительно, то неравенство ![]() выполняется, если множители х - 1 и х + 2/7 имеют противоположные знаки. Рассмотрим два случая.
выполняется, если множители х - 1 и х + 2/7 имеют противоположные знаки. Рассмотрим два случая.
1) Пусть х – 1 ≥ 0 и х + 2/7 ≤ 0. Получаем систему линейных неравенств 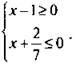 Решая систему, имеем
Решая систему, имеем 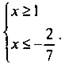 Такая система решений не имеет.
Такая система решений не имеет.
2) Пусть х – 1 ≤ 0 и х + 2/7 ≥ 0. Получаем систему линейных неравенств 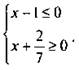 Решая систему, имеем
Решая систему, имеем 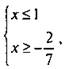 откуда -2/7 ≤ х ≤ 1.
откуда -2/7 ≤ х ≤ 1.
Итак, решениями неравенства ![]() а следовательно, и неравенства -7х2 + 5х + 2 ≥ 0 являются все числа из промежутка -2/7 ≤ х ≤ 1.
а следовательно, и неравенства -7х2 + 5х + 2 ≥ 0 являются все числа из промежутка -2/7 ≤ х ≤ 1.
Такой же подход можно использовать и при решении квадратных неравенств с параметрами.
Пример 6
Решим неравенство ![]() .
.
Найдем корни квадратного уравнения ![]() и получим
и получим ![]() т. е. х1 = 1, х2 = 2. Разложим квадратный трехчлен на множители и получим неравенство (х – a)(x _ 2) ≤ 0. Произведение множителей отрицательно, если множители х - a и х - 2 имеют противоположные знаки. При этом важно, какое из чисел а и 2 больше. Поэтому необходимо рассмотреть три случая.
т. е. х1 = 1, х2 = 2. Разложим квадратный трехчлен на множители и получим неравенство (х – a)(x _ 2) ≤ 0. Произведение множителей отрицательно, если множители х - a и х - 2 имеют противоположные знаки. При этом важно, какое из чисел а и 2 больше. Поэтому необходимо рассмотреть три случая.
1) Пусть а < 2. Тогда получаем две системы линейных неравенств: ![]() или
или ![]() (такая система решений не имеет, т. к. а < 2) и
(такая система решений не имеет, т. к. а < 2) и ![]() или
или ![]() (решение этой системы а ≤ х ≤ 2). Итак, при а < 2 решение данного неравенства а ≤ х ≤ 2.
(решение этой системы а ≤ х ≤ 2). Итак, при а < 2 решение данного неравенства а ≤ х ≤ 2.
2) Пусть a = 2. Подставим это значение в данное неравенство и получим: х2 - 4х + 4 ≤ 0 или (х - 2)2 ≤ 0. Очевидно, что такое неравенство имеет решение х = 2 (при остальных х выражение (х - 2)2 > 0). Итак, при a = 2 решение данного неравенства х = 2.
3) Пусть a > 2. Тогда получаем две системы линейных неравенств: ![]() или
или ![]() (решение этой системы 2 ≤ х ≤ a) и
(решение этой системы 2 ≤ х ≤ a) и ![]() или
или ![]() (такая система решений не имеет, т. к. а > 2). Итак, при а > 2 решение данного неравенства 2 ≤ х ≤ а.
(такая система решений не имеет, т. к. а > 2). Итак, при а > 2 решение данного неравенства 2 ≤ х ≤ а.
Так как в задачах с параметрами очень важен правильный ответ, то выпишем ответ данной задачи: при а < 2 а ≤ х ≤ 2, при а = 2х = 2, при а > 2 2 ≤ х ≤ а.
Заметим, что аналогичный подход можно использовать и при решении неравенств с модулями. При этом надо помнить, что при возведении в квадрат неотрицательных частей неравенства знак неравенства сохраняется и получается равносильное неравенство (т. е. имеющее те же решения, что и данное неравенство). Учитывая свойство модуля |а| = а2, отпадает необходимость раскрытия модуля.
Пример 7
Решим неравенство ![]()
Возведем в квадрат обе неотрицательные части данного неравенства и получим: ![]() или
или ![]() (при этом знак модуля исчезает). Перенесем все члены неравенства в левую часть
(при этом знак модуля исчезает). Перенесем все члены неравенства в левую часть ![]() Используя формулу разности квадратов, разложим эту часть на множители. Имеем:
Используя формулу разности квадратов, разложим эту часть на множители. Имеем: ![]() или
или ![]() или
или ![]() Произведение множителей положительно, если множители х - 2 и х + 1 имеют одинаковые знаки. Получаем две системы линейных неравенств.
Произведение множителей положительно, если множители х - 2 и х + 1 имеют одинаковые знаки. Получаем две системы линейных неравенств.
1) ![]() или
или ![]() Решение этой системы х > 2.
Решение этой системы х > 2.
2) ![]() или
или ![]() Решение этой системы х < -1.
Решение этой системы х < -1.
Итак, решение данного неравенства х < -1 и х > 2.
Пример 8
Решим неравенство ![]()
Возведем в квадрат обе неотрицательные части данного неравенства и получим: ![]() или
или ![]() (при этом знаки модулей исчезают). Перенесем все члены неравенства в левую часть
(при этом знаки модулей исчезают). Перенесем все члены неравенства в левую часть ![]() Используя формулу разности квадратов, разложим эту часть на множители. Имеем:
Используя формулу разности квадратов, разложим эту часть на множители. Имеем: ![]() или
или ![]() или
или ![]() Произведение множителей отрицательно, если множители 2 - х и 3х - 1 имеют разные знаки. Получаем две системы линейных неравенств.
Произведение множителей отрицательно, если множители 2 - х и 3х - 1 имеют разные знаки. Получаем две системы линейных неравенств.
1) ![]() или
или 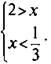 Решение этой системы x < 1/3.
Решение этой системы x < 1/3.
2) 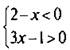 или
или 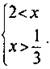 Решение этой системы х > 2.
Решение этой системы х > 2.
Итак, решение данного неравенства х < 1/3 и х > 2.
III. Контрольные вопросы
1. Какое неравенство называется квадратным? Приведите примеры.
2. Что называется решением неравенства с одной переменной?
3. Что значит решить неравенство?
4. Как решают квадратное неравенство (опишите алгоритм)?
IV. Задание на уроке
№ 649; 650 (1, 4); 651 (1, 2); 652 (2, 3); 653 (1, 4); 654 (5); 655 (1, 4); 657.
V. Задание на дом
№ 650 (2, 3); 651 (3, 4); 652 (1,4); 653 (2, 3); 654 (6); 655 (2, 3); 658.
VI. Творческие задания
1. При всех значениях параметра а решите неравенство:
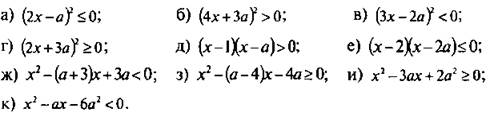
Ответы: а) при всех а х = a/2;
б) при всех а х — любое число, кроме х = -3/4а;
в) при всех а решений нет;
г) при всех а х — любое число;
д) при а < 1 х < а и х > 1, при а = 1 х — любое число, кроме х = 1, при а > 1 х<1 и х > a;
е) при а < 1 2а ≤ х ≤ 2, при а = 1 х = 2, при а > 1 2 ≤ х ≤ 2а;
ж) при а< 3 a < x < 3, при а = 3 решений нет, при а > 3 3 < х < a;
з) при а < -4 х ≤ а и х ≥ -4, при а = -4 х — любое число, при а > -4 х ≤ -4 и х ≥ a;
и) при a > 0 х ≤ 2а и х ≥ a, при a = 0 х — любое число, при a > 0 х ≤ a и х ≥ 2a.
к) при а < 0 3а < х < -2а, при а = 0 решений нет, при а > 0 -2а < х < 3а.
2. Решите неравенство:
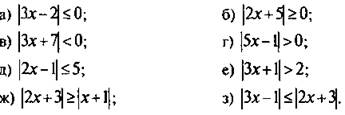
Ответы: а) х = 2/3; б) х — любое число; в) решений нет; г) x — любое число, кроме х = 1/5.
![]()
VII. Подведение итогов урока