Поурочные разработки по алгебре для 8 класса к учебнику Ю.Н. Макарычева
Графическое решение квадратного неравенства - РЕШЕНИЕ КВАДРАТНОГО НЕРАВЕНСТВА С ПОМОЩЬЮ ГРАФИКА КВАДРАТИЧНОЙ ФУНКЦИИ - КВАДРАТНЫЕ НЕРАВЕНСТВА
Цель: рассмотрение графического способа решения квадратного неравенства.
Ход урока
I. Сообщение темы и цели урока
II. Повторение и закрепление пройденного материала
1. Ответы на вопросы по домашнему заданию (разбор нерешенных задач).
2. Контроль усвоения материала (тест).
Вариант I
1. Решите неравенство ![]()
Ответы: ![]()
2. Решите неравенство 2х2 - 3х + 1 ≤ 0.
Ответы: ![]()
3. Решите неравенство |3х - 4| > 1.
Ответы: ![]()
Вариант 2
1. Решите неравенство ![]()
Ответы: ![]()
2. Решите неравенство 3х2 - 5х + 2 ≤ 0.
Ответы: ![]()
3. Решите неравенство |2х - 3| > 1.
Ответы: а) х > 1; б) х > 2; в) 1 < х < 2; г) х < 1 и х > 2.
III. Изучение нового материала (основные понятия)
Как известно, квадратичная функция задается формулой у = ax2 + bх + с (где а ≠ 0) и ее графиком является парабола. Поэтому графическое решение квадратного неравенства сводится к отысканию нулей квадратичной функции, построению эскиза графика этой функции и отысканию промежутков, на которых квадратичная функция принимает положительные или отрицательные значения.
Пример 1
Графически решим неравенство х2 – х – 2 ≥ 0.
Графиком квадратичной функции у = х2 – х - 2 является парабола, ветви которой направлены вверх. Найдем точки пересечения этой параболы с осью Ох. Для этого решим квадратное уравнение х2 – х - 2 = 0. Корни этого уравнения ![]() т. е. х1 = -1 и х2 = 2. Следовательно, парабола пересекает ось Ох в точках х = -1 и х = 2. Изобразим эскиз графика этой квадратичной функции.
т. е. х1 = -1 и х2 = 2. Следовательно, парабола пересекает ось Ох в точках х = -1 и х = 2. Изобразим эскиз графика этой квадратичной функции.
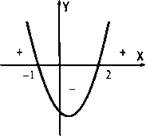
Неравенству х2 – х – 2 ≥ 0 удовлетворяют те значения х, при которых значения функции равны нулю или положительны, т. е. те значения х, при которых точки параболы лежат на оси Ох или выше этой оси. Из рисунка видно, что такими значениями являются все числах из промежутков х ≤ -1 и х ≥ 2.
График построенной функции может быть использован и при решении других неравенств, которые отличаются от данного только знаком неравенства. Из приведенного рисунка видно, что:
1) решениями неравенства х2 – х – 2 > 0 являются числа из промежутков х < -1 и х > 2;
2) решениями неравенства х2 - х - 2 ≤ 0 являются все числа промежутка -1 ≤ х ≤ 2.
3) решениями неравенства х2 - х - 2 < 0 являются все числа промежутка -1 < х < 2.
Заметим, что при решении квадратных неравенств необязательно приводить их к стандартному виду. Еще раз вернемся к предыдущему примеру и решим его несколько иначе.
Пример 2
Вновь решим неравенство х2 - х - 2 ≥ 0. Представим такое неравенство в виде х2 ≥ х + 2. В одной и той же системе координат построим графики функций у1 = х2 (парабола) и у2 = х + 2 (прямая линия). Найдем абсциссы точек пересечения этих графиков. Приравняем правые части функций и получим уравнение: х2 = х + 2 или х2 - х - 2 = 0. Корни этого квадратного уравнения х1 = -1 и х2 = 2. Поэтому такие графики пересекаются в двух точках А и В, абсциссы которых, соответственно, равны x1 = -1 и x2 = 2.
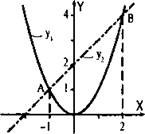
Неравенству x2 ≥ x + 2 или y1 ≥ y2 удовлетворяют те значения x, при которых значения первой функции больше или равны значениям второй функции, т. е. при которых график первой функции расположен выше или на уровне второй функции. Из рисунка видно, что такими значениями являются все числа jc из промежутков x1 ≤ -1 и х2 ≥ 2.
Несмотря на различие рисунков в примерах 1 и 2, получен один и тот же результат, т. е. одно и то же решение данного неравенства. Заметим, что второй способ оказывается более полезным при решении сложных неравенств (кубических неравенств, неравенств с модулями и т. д.).
Пример 3
Решим неравенство -x2 + 2x – 1 ≥ 0.
Запишем неравенство в виде –(x - 1)2 ≥ 0 и построим эскиз графика функции y = -(x – 1)2. Ветви этой параболы направлены вниз. Уравнение -(х – 1)2 = 0 имеет один корень х = 1. Поэтому парабола касается оси Ох в точке (1; 0). Для решения неравенства - (х - 1)2 ≥ 0 надо определить, при каких значениях х функции у неотрицательны.
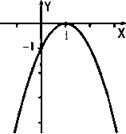
Из рисунка видно, что функция положительных значений не имеет. Значение у = 0 получается только при х = 0. Поэтому данное неравенство -х2 + 2x - 1 ≥ 0 имеет единственное решение х = 1.
Разумеется, как и в примере 1, используя построенный график, можно решить и аналогичные неравенства.
Пример 4
Решим неравенство 2х2 - 4х + 3 > 0.
Построим эскиз графика функции у = 2х2 - 4х + 3. Ветви этой параболы направлены вверх. Уравнение 2x2 – 4x + 3 = 0 корней не имеет, поэтому парабола не пересекает ось Ох. Это означает, что значения квадратичной функции при всех х положительны. Поэтому неравенство 2х2 - 4х + 3 > 0 выполняется при всех значениях х.
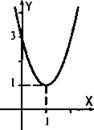
Для решения квадратного неравенства с помощью графика нужно:
1) определить направление ветвей параболы по знаку старшего коэффициента квадратичной функции;
2) найти корни соответствующего квадратного уравнения или установить, что их нет;
3) построить эскиз графика квадратичной функции, учитывая точки пересечения (или касания) с осью Ох, если они есть;
4) по графику определить промежутки, на которых функция принимает нужные значения.
Разумеется, используя рассмотренные подходы, можно решать и более сложные неравенства.
Пример 5
Решим неравенство х2 - 2х + 1 < |х + 1|.
Учитывая формулу квадрата разности, запишем данное неравенство в виде (x – 1)2 < |x + 1|. Построим графики функций y1 = (x – 1)2 и y2 = |х + 1|.
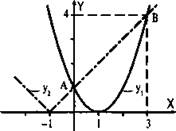
График функции у1 представляет собой параболу у = х2, смещенную на одну единицу вправо. График функции у2 —зависимость y = |x|, смещенная на одну единицу влево. Видно, что графики функций пересекаются в двух точках, причем абсциссы этих точек больше числа -1. Учитывая, что х > -1, для нахождения абсцисс точек пересечения получаем уравнение: (x – 1)2 = x + 1 (т. к. |х + 1| = х + 1 при х > -1), или х2 - 2х + 1 = х + 1 или х2 - 3х = 0. Корни этого уравнения x1 = 0 и х2 = 3. Неравенству х2 - 2х + 1 < |х + 1| или у1 < у2 удовлетворяют те значения х, при которых значения первой функции меньше значений второй функции, т. е. при которых график первой функции расположен ниже графика второй функции. Из рисунка видно, что такими значениями являются все х из промежутка 0 < х < 3.
Такими же способами могут быть решены и квадратные неравенства с параметрами.
Пример 6
При каких значениях параметра а неравенство х2 + 3ах + 4 > 0 выполняется при всех действительных значениях х?
Рассмотрим квадратичную функцию у = х2 + 3ах + 4. Графиком этой функции будет парабола, направленная ветвями вверх. Значения квадратичной функции положительны при всех значениях х, если дискриминант квадратного трехчлена х2 + 3ах + 4 отрицательный (тогда парабола не пересекает ось Ох). Найдем дискриминант D = 9a2 - 16. Получаем квадратное неравенство 9a2 - 16 < 0. Решим его графическим способом.
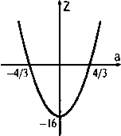
Построим график функции z = 9a2 - 16. Этот график пересекает горизонтальную ось в точках a = ±4/3 и направлен ветвями вверх. Из рисунка видно, что значения z < 0 при всех а из промежутка -4/3 < a < 4/3 (масштаб на графике искажен).
Пример 7
При каких значениях параметра а неравенство (a - 1)х2 - 2х + (a - 1) ≤ 0 выполняется при всех действительных значениях х?
Рассмотрим квадратичную функцию у = (a - 1)х2 - 2х + (а - 1). Графиком этой функции будет парабола, направление ветвей которой определяется старшим коэффициентом а - 1. По аналогии с предыдущей задачей легко сообразить, что квадратичная функция будет принимать неположительные значения (т. е. парабола будет располагаться ниже оси Ох или касаться ее) при выполнении двух условий:
1) старший коэффициент отрицательный (т. е. парабола направлена ветвями вниз), т. е. а – 1 < 0 или а < 1;
2) дискриминант квадратного трехчлена неположительный (т. е. парабола не пересекает оси Ох или касается ее), т. е. D/4 ≤ 0.
Займемся последним неравенством. Получаем: ![]()
![]() Решая это неравенство любым способом, получаем а ≤ 0 и а ≥ 2. С учетом условия а < 1 находим, что при а ≤ 0 условия задачи выполняются.
Решая это неравенство любым способом, получаем а ≤ 0 и а ≥ 2. С учетом условия а < 1 находим, что при а ≤ 0 условия задачи выполняются.
IV. Контрольные вопросы
1. Как построить график квадратичной функции (в случае затруднения объясните на конкретном примере)?
2. Как использовать график квадратичной функции для решения квадратного неравенства (можно объяснить на конкретном примере)?
V. Задание на уроке
№ 660 (2); 662 (1); 663 (1, 2); 664 (3); 665 (а, б, г); 666 (1,4); 670 (2); 671.
VI. Задание на дом
№ 661 (3); 662 (5); 663 (3,4); 664 (5); 665 (д, е, ж); 666 (2, 3); 670 (4); 673.
VII. Творческие задания
1. Решите неравенства:
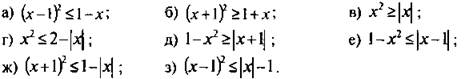
Ответы: ![]()
![]()
2. При каких значениях параметра а неравенство выполняется при всех значениях x:
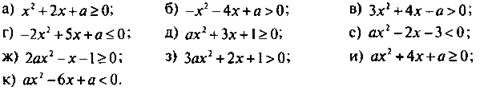
Ответы: а) а ≥ 1; б) а < -4; в) а < -4/3; г) a ≤ -25/8; д) a ≥ 9/7; е) a < -1/3; ж, з) таких а нет; и) а ≥ 2; к) а < -3.
VIII. Подведение итогов урока