Зачетная работа по теме «Квадратные неравенства» - МЕТОД ИНТЕРВАЛОВ - КВАДРАТНЫЕ НЕРАВЕНСТВА

Цель: проверка знаний учащихся по вариантам одинаковой сложности.

Ход урока

I. Сообщение темы и цели урока

II. Характеристика зачетной работы

По сравнению с контрольной работой в зачетной увеличено количество заданий. Соответственно, у учащихся возрастает возможность выбора задач. Все задания разбиты на три блока А, В и С. Самые простые задачи находятся в части А, более сложные — в части В, еще сложнее — в части С. Каждая задача из А оценивается в 1 балл, из В — в 2 балла, из С — в 3 балла. Поэтому за правильное решение всех задач блока А можно получить 7 баллов, блока В — 8 баллов и блока С — 9 баллов (всего 24 балла). Оценка «3» ставится за 6 баллов, оценка «4» — за 10 баллов, оценка «5» — за 14 баллов.

Так как эта работа является зачетной, то в нее не включены принципиально новые задачи. Поэтому разбору заданий работы отдельного занятия можно и не посвящать (решения задач могут быть вывешены на стенде). Для стендового размещения разбор заданий приводится.

III. Задания зачетной работы

А

Решите неравенство:

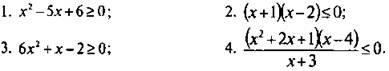
5. Найдите все решения неравенства принадлежащие промежутку -2 ≤ х ≤ 2.

6. При каких значениях х имеет смысл выражение

7. Графически решите неравенство

В

8. Докажите, что дробь при всех х принимает положительные значения.

9. Найдите область определения выражения

10. При каких значениях параметра а число 4 удовлетворяет неравенству

11. Решите неравенство

С

12. Решите неравенство

13. Найдите наименьшее целое значение переменной а, при котором имеет смысл выражение

14. При каких значениях параметра а неравенство выполняется при всех значениях х?

IV. Разбор заданий зачетной работы

1. Ответ: х ≤ 2, х ≥ 3. .

2. Ответ: -1 ≤ х ≤ 2.

3. Ответ: х ≤ -2/3, х ≥ 1/2. .

4. Ответ: -3 < х ≤ 4.

5. Ответ: -1,5 ≤ х ≤ 2. .

6. Ответ: х ≤ 0, х ≥ 6.

7. Ответ: —3 < х < 1.

8. Указание: в знаменателе дроби выделить полный квадрат разности. Ответ: доказано.

9. Ответ: х < -3, -3 < х ≤ 2, 7/3 ≤ х < 3, х > 3.

10. Ответ: а ≤ 2,3.

11. Ответ: 0 < х < 1, х = 3.

12. Решим неравенство методом интервалов. Сначала найдем корни многочлена. Введем новую переменную t = x2 - 5 и получим квадратное уравнение t2 – 10t - 11 = 0, корни которого t1 = -1 и t2 = 11. Вернемся к переменной х и имеем уравнение: х2 - 5 = -1 (корни х1,2 = ±2) и х2 -5 = 11 (корни х3,4 = ±4). Отметим эти корни на числовой оси и расставим знаки в промежутках.

На основании диаграммы знаков выписываем ответ: -4 ≤ х ≤ -2, 2 ≤ х ≤ 4.

13. Данное выражение имеет смысл, если подкоренные выражения неотрицательны. Получаем систему квадратных неравенств Решая каждое из неравенств системы, найдем Поэтому решение системы неравенств -5 ≤ а ≤ -4; -1,5 ≤ а ≤ 2. Наименьшее целое значение переменной а, входящей в эти промежутки, а = -5.

Ответ: а = -5.

14. Очевидно, что данное неравенство выполняется при всех значениях x, если дискриминант квадратного трехчлена отрицательный. Найдем Получаем неравенство а2 – а – 6 < 0, его решение -2 < а < 3.

Ответ: -2 < а < 3.