Поурочные разработки по Алгебре 8 класс
Урок 1 - ТЕОРЕМА ВИЕТА
Цели: повторить формулы для решения квадратных уравнений; доказать теорему Виета, показать ее применение; рассмотреть различные задания на применение теоремы Виета; сформировать умение использовать эту теорему.
Ход урока
I. Организационный момент.
II. Актуализация знаний.
На доске рассмотреть решение уравнений по двум различным формулам, найти для каждого уравнения сумму и произведение корней:
а) x2 – x – 6 = 0;
б) x2 – 8x – 20 = 0.
III. Объяснение нового материала.
Обратить внимание учеников на то, что объединяет решенные уравнения. Затем на доске записывается теорема Виета и доказывается учителем согласно параграфу.
IV. Закрепление нового материала.
1) Определить знаки корней данных уравнений:
а) x2 – 9x – 10 = 0; б) x2 + 5x + 6 = 0;
в) x2 + 4x – 5 = 0; г) x2 – 5x + 4 = 0.
Например: x2 + 4x – 12 = 0.
В данном уравнении произведение корней равно –12, значит один из корней положительный, а другой отрицательный. Так как сумма корней данного уравнения равна –4, то отрицательное число больше по модулю.
2) Решить уравнения № 29.3; 29.5; 29.7; 29.10; 29.12; 29.14.
3) Один из корней уравнения равен –2. Найдите коэффициент a и второй корень уравнения:
а) x2 + 5x + a = 0;
б) x2 + ax – 20 = 0.
4) Для сильных учеников предлагается задание:
Пусть x1 и x2 корни уравнения x2 + px + q = 0, найдите значения выражений (вспомнить, каким образом аналогичное задание решалось ранее, сделать выводы):
а) 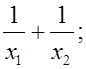 б) (x1 + x2)2; в)
б) (x1 + x2)2; в) ![]()
Р е ш е н и е:
а) 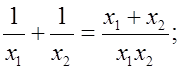
По теореме Виета из уравнения x2 + px + q = 0 следует 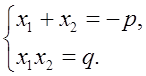
Значит, 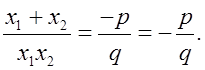
в) ![]()
![]()
V. Подведение итогов.
Домашнее задание: решить задания № 29.2; 29.6; 29.9; 29.13.