Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003

Указания
Первые указания

K главе 1

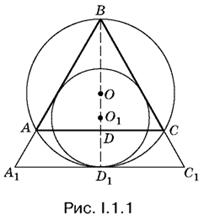
1.1. Если через точку D₁ касания окружностей провести их общую касательную, то, пересекая продолжения сторон ВА₁ и ВС₁, она образует треугольник А₁ВС₁ (рис. I.1.1). Воспользуйтесь тем, что OD = DD₁ = ^R/₂, а O₁D₁ = ^BD₁/₃.

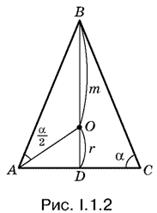
1.2. В треугольнике АОВ (O — центр вписанной окружности, рис. I.1.2) угол ВАО равен ^α/₂ , а угол ВОА равен сумме углов OAD и ODA, т. е. равен ^π/₂ + ^α/₂ . По условию BO = m, так как BD = r + m. Поэтому решение удобно начать с определения AB из треугольника BOA.

1.3. Вначале нужно выяснить смысл выражения «окружность делит сторону треугольника пополам». Если окружность имеет со стороной треугольника две общие точки, то ни про одну мы не сможем сказать, что она делит отрезок пополам, поскольку отрезок разделится на три части.

1.4. Отношение площади треугольника А₁В₁С₁ к площади треугольника АВС (рис. I.1.4) можно записать так:

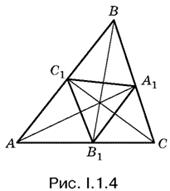
Теперь нужно найти каждое из отношений, входящих в правую часть.

1.5. Углы определяют треугольник лишь с точностью до подобия. Если ввести в рассмотрение один линейный элемент и выразить через него обе площади, то при подсчете отношения площадей этот элемент сократится. В качестве такого линейного элемента удобно выбрать радиус r вписанной в треугольник окружности.

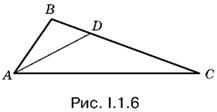
1.6. Так как В = 3C (рис. I.1.6), то сторона AB меньше стороны AC и можно доказать, что площадь треугольника АВD (АD — биссектриса треугольника АВС) меньше площади треугольника ADC. Таким образом по условию

1.7. Применить метод сравнения площадей.

1.8. Все участвующие в задаче величины связаны с площадью треугольника, которая известна. Воспользоваться сравнением площадей.

1.9. В треугольнике даны две биссектрисы и отношение, в котором эти биссектрисы делятся точкой их пересечения. Наряду с данными отношениями естественно воспользоваться свойством отрезков, на которые биссектриса делит противоположную сторону треугольника. Поскольку требуется определить углы треугольника, то от отношений данных линейных величин нужно перейти к отношению сторон данного треугольника.

1.10. Продолжить отрезок QМ до пересечения в точке А с другой стороной угла.

1.11. Известные высоты треугольника естественно связать между собой с помощью его площади. При этом вместо сторон треугольника удобнее рассматривать его углы, выразив стороны через третью высоту.

1.12. В соотношении b + с = k выразить b и с через известную высоту h и тригонометрические функции углов В и С.

1.13. Способ 1. Чтобы решить задачу, нужно установить связь между углом α, сторонами треугольника и его площадью. Однако установить эту связь непосредственно не удается. Поэтому необходимо рассматривать вспомогательные элементы, например перпендикуляры длины x, у и z, опущенные из точки О на стороны а, b, с соответственно.

Способ 2. Чтобы установить связь между углом α, сторонами треугольника и его площадью, можно ввести в рассмотрение длины отрезков: ОА = I, ОВ = m, ОС = n.

1.14. По условию CD = BC − AC (D — основание высоты). Однако BC и AC можно выразить через CD с помощью тригонометрических функций углов треугольника АВС. Это даст нам уравнение, связывающее углы треугольника АВС.

1.15. Если рассматривать длины сторон AC = b и BC = а, то все участвующие в задаче геометрические величины будут связаны с площадью треугольника ABC.

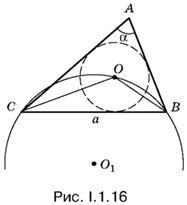
1.16. Чтобы геометрически связать окружность с центром О и окружность с центром О₁, нужно провести отрезки СО и ВО (рис. I.1.16). Окружность О₁ описана около треугольника СОВ. Длина хорды СВ известна. Следовательно, для того, чтобы найти радиус, достаточно определить угол СОВ.

1.17. Задачу удобно переформулировать иначе: через центр вписанной окружности проведем прямую, параллельную средней стороне треугольника, и докажем, что она пройдет через точку пересечения медиан, т. е. точка пересечения этой прямой с медианой, опущенной на меньшую сторону, делит медиану в отношении 2 : 1.

1.18. Воспользоваться методом сравнения площадей.

1.19. Точки A, О и L лежат на одной прямой — биссектрисе угла ВАС, аналогично точки В, О и K лежат на биссектрисе угла АВС. Прямая KL делит угол АСМ пополам (СМ — продолжение BC).

По условию A = 2С, а В = 4С (рисунок сделайте самостоятельно).

1.20. Так как сумма углов в треугольнике равна π, то углы А, В и С нетрудно вычислить.

1.21. Сделать несложное дополнительное построение, чтобы получились подобные треугольники.

1.22. Поскольку отрезки, длины которых входят в правую часть равенства, лежат на одной прямой, нужно выразить длины всех отрезков на той же прямой. Тем самым мы «спрямим» записанное соотношение и сделаем его доказательство простым.

1.23. В формулу входят отношения. Поэтому целесообразно сделать дополнительные построения, в результате которых получатся подобные треугольники.

1.24. При построении, описанном в условии, возникают подобные треугольники. Нужно с их помощью заменить стоящие в левой части отношения новыми отношениями с тем, чтобы в знаменателе была одна и та же сторона треугольника, а в числителе — отрезки этой стороны. (!)

1.25. Положение прямой, проходящей через точку О, можно определить с помощью угла α, который эта прямая составляет с некоторым фиксированным радиусом описанной окружности. Нужно доказать, что величина, о которой говорится в условии, не зависит от α.

1.26. Чтобы ответить на вопрос задачи, нужно знать стороны данного треугольника и радиус описанной около него окружности. С вычисления этих величин и следует начать решение задачи.

1.27. Связать углы треугольника и его стороны можно либо с помощью теоремы синусов, либо с помощью теоремы косинусов. Данное в условии соотношение между сторонами треугольника подсказывает, что теорема косинусов удобнее.

1.28. Если отрезки ОА, ОВ и ОС, входящие в данное соотношение ОА² = ОВ · ОС, выразить через радиус r вписанной окружности и углы треугольника, то должно получиться соотношение между тригонометрическими функциями этих углов, не содержащее r. (!)

1.29. Применить формулу, выражающую площадь треугольника через две стороны и синус угла, и теорему косинусов. (!)

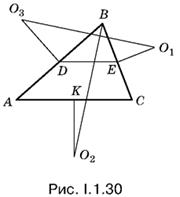
1.30. Чтобы доказать равенство двух отрезков, о которых идет речь в условии, можно ввести элементы, определяющие треугольник, и выразить через них эти отрезки. То же самое можно сделать геометрически: четырехугольник О₁ЕDО₃ (рис. I.1.30), построенный на отрезке О₁О₃, таков, что каждая из трех его остальных сторон равна половине соответствующей стороны треугольника. Остается построить такой же четырехугольник на отрезке ВО₂.

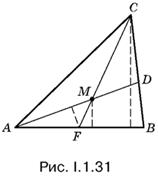
1.31. Площадь треугольника АFМ (рис. I.1.31) в восемь раз меньше площади треугольника АВС, так как АF = ½AB, а высота треугольника АFМ в четыре раза меньше высоты треугольника АВС (докажите). Если рассматривать AM и АD как основания треугольников АFМ и АВD, то соответствующие высоты этих треугольников относятся как 1 : 2. Выяснив, в каком отношении точка M делит отрезок АD, мы решим задачу.

1.32. Так как четырехугольник вписанный, то кроме входящих в задачу величин целесообразно рассмотреть радиус круга R и углы четырехугольника. Введя углы, мы сможем использовать свойство вписанного четырехугольника.

1.33. Использовать тот факт, что боковые стороны трапеции и отрезок, соединяющий середины ее оснований, лежат на прямых, пересекающихся в общей точке.

1.34. Если обозначить сторону квадрата через а, а расстояние от точки M до самой ближней стороны (либо до AB, либо до CD) через x, то остальные расстояния можно выразить через а и x.

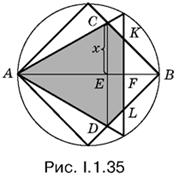
1.35. Фигура, площадь которой нужно определить, на рис. I.1.35 заштрихована. Отрезок CD разбивает эту фигуру на правильный треугольник и трапецию. Длина отрезка АF известна, она равна ³/₂. Если мы сможем определить длину отрезка СЕ (обозначим ее x), то задача будет решена.

1.36. Из параллельности сторон трапеции и треугольника следует, что углы при основании треугольника и при нижнем основании трапеции равны. Если обозначить эти углы через α, то можно выразить через α и другие углы, связанные с треугольником и трапецией.

1.37. Треугольники АОD и BОС подобны. Это позволяет из отношения оснований трапеции получить отношение высот треугольника АОD и трапеции. (!)

1.38. Нас интересует периметр третьего многоугольника. Обозначим его через x. Введем также радиус окружности R и число сторон b первого многоугольника.

1.39. Окружность не может лежать между точками M и О (докажите). Ее центр О₁ лежит на биссектрисе угла АОВ.

1.40. Из данного отношения площадей треугольников АВС и АDЕ, записанного в виде отношения произведений катетов, и из свойства произведения секущей на ее внешнюю часть найти отношение ^AE/_AB.

1.41. Пусть О₁ — центр окружности, радиус которой мы ищем, а О — центр данной окружности. В качестве связующего звена следует рассмотреть треугольник АОО₁.

1.42. Нужно обозначить сторону квадрата через а и составить с помощью теоремы Пифагора биквадратное уравнение для определения а через R и r.

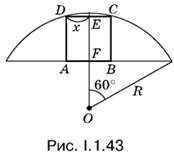
1.43. Вписанный в сегмент квадрат не должен нарушать симметрии сегмента. Поэтому он расположится так, как показано на рис. I.1.43. Обозначим половину стороны квадрата через x и составим уравнение относительно x.

1.44. Чтобы использовать условия задачи, нужно провести радиусы обеих окружностей в точки касания окружностей друг с другом и с нижним основанием. Центр меньшей окружности лежит на биссектрисе угла D.

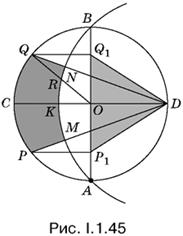
1.45. Вначале для определенности удобно предположить, что точки P и Q лежат по разные стороны от CD. В этом случае диаметр CD разделит фигуры РQNМ и Р₁Q₁D на две части (рис. I.1.45). Нужно доказать, что площадь фигуры СQNK равна площади треугольника Q₁OD. При этом полезен будет следующий факт. Если соединить точки Q и О, то, во-первых, угол QОС вдвое больше угла QDС, а во-вторых, треугольники ОQ₁D и ОQD равновелики.

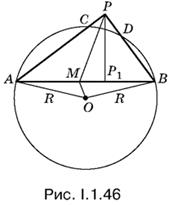
1.46. Соединим точки А и В, P и M и проведем радиусы из центра О в точки А и В (рис. I.1.46). Если длины отрезков AB, АР₁ и ОА = R заданы и отрезок AB построен, то прямоугольный треугольник АРВ и положение точки О определяются однозначно. Следовательно, зная длины этих отрезков, можно вычислить длины интересующего нас отрезка РМ.

1.47. Отрезок, соединяющий центр окружности с серединой хорды, перпендикулярен к этой хорде. Зная, что хорда удалена от центра на ^3R/₅, легко выразить ее длину через R.

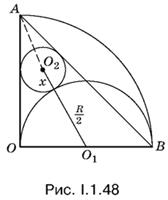
1.48. Использовать геометрически касание окружности О₂ с окружностью О₁ можно, соединив их центры (рис. I.1.48). Отрезок О₂О₁ пройдет через точку касания. Так как окружность О₂ касается сторон угла ОАВ, то ее центр лежит на биссектрисе угла ОАВ.

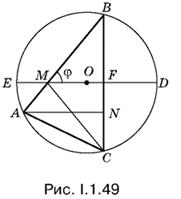
1.49. Если в треугольнике АВС провести высоту АN (рис. I.1.49), то искомая площадь будет равна ½АN · BC. Соединив точки M и С, разобьем треугольник АВС на равнобедренный треугольник МСВ и треугольник АМС, у которого угол АМС легко выразить через φ.

1.50. Задача вычислительная. Нужно воспользоваться формулой Герона и выражением радиуса R через стороны треугольника и его площадь S, т. е. R = ^abc/_4S . Стороны треугольника удобно обозначить: а, а − d, а + d.

1.51. Проведите через точки P и Q прямые, параллельные AC. Первая будет средней линией треугольника АВС, вторая — средней линией треугольника с вершиной В, которому первая средняя линия служит основанием.

1.52. Соединим точки P и T. Данный треугольник разбивается на пять. Пусть QT = m, TL = n, QN = RL = а. Чтобы использовать условия задачи, можно записать соотношения площадей различных треугольников, образовавшихся из данного треугольника PQR.

1.53. Хорда MN — сторона правильного шестиугольника, вписанного в первую окружность, так как опирающийся на MN центральный угол ∠МО₁N = 60°. Чем является MN для второй окружности?

1.54. Для вписанного в окружность четырехугольника воспользоваться свойством, в силу которого сумма противоположных его углов равна 180°. Удобно обозначить стороны четырехугольника через а, b, с, d, начиная со стороны AB, а опирающиеся на них углы (проведите диагонали) через α, β, γ, δ.

K главе 2

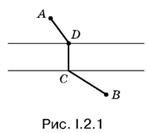
2.1. Предположим, что где-то построен мост (рис. I.2.1). В этом случае путь из А в В будет ломаной, состоящей из трех звеньев. Среднее звено всегда остается неизвестным по длине и направлению. Следовательно, нужно «спрямить» первое и третье звенья.

2.2. Из точки А отрезки МР и РN видны под углом 30° каждый. Следовательно, построить точку А можно как пересечение двух сегментов, вмещающих угол в 30°.

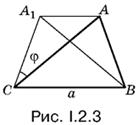
2.3. Пусть треугольник АВС искомый (рис. I.2.3). Чтобы на чертеже появился угол φ, отразим треугольник АВС от вертикальной оси, проходящей через середину BC. Получим треугольник СА₁А, в котором ∠А₁СА = φ.

2.4. В любом треугольнике АВС центр описанной окружности лежит на пересечении перпендикуляров, восставленных из середин сторон. Этот факт можно использовать для того, чтобы связать данные элементы треугольника: b и m_с.

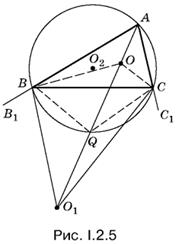
2.5. Точки О (центр вписанной окружности) и О₁ (центр вневписанной окружности) лежат на биссектрисе угла А треугольника АВС (рис. I.2.5). Отрезки ОС и О₁С, ОВ и О₁В взаимно перпендикулярны как биссектрисы смежных углов. Поэтому точки В, О, С, О₁ лежат на одной окружности с центром в точке Q.

2.6. Применить метод подобия, выбрав за центр подобия одну из вершин треугольника, А или С.

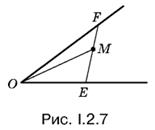
2.7. Если прямую FЕ (рис. I.2.7) вращать около точки M, то площади треугольников ОМF и ОМЕ будут изменяться так, что с увеличением одной уменьшается другая. Это должно навести на мысль рассмотреть некоторое среднее положение.

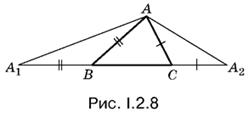
2.8. Чтобы использовать данный в условии периметр треугольника, нужно осуществить «спрямление», т. е. рассмотреть треугольник, который получается из искомого, если отложить на BC отрезки А₁В и СА₂, равные AB и AC соответственно, так, как это показано на рис. I.2.8.

2.9. Чтобы подойти к решению задачи, нужно построить из отрезков АР, ВР и СР ломаную с закрепленными концами и посмотреть, когда эта ломаная будет выпрямляться.

2.10. Зная гипотенузу, можно построить окружность, в которую вписан искомый прямоугольный треугольник АВС. Если биссектрису CD продолжить до пересечения с этой окружностью в точке E, то получим две равные дуги АЕ и ЕВ. Следовательно, отрезок ОЕ, соединяющий точку E с центром круга, перпендикулярен к AB и равен ^c/₂. Теперь все данные в условии элементы связаны между собой.

2.11. Пусть известны углы при вершинах А и D четырехугольника и его стороны AB = а, BC = b, CD = с. Если угол ВАD закреплен, то положение точки С определяется с помощью метода геометрических мест.

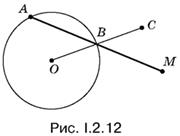
2.12. Пусть AM (рис. I.2.12) — искомая секущая и AB = ВМ. Чтобы связать ее с данной окружностью, соединим точки О и В. Если отрезок ОВ продолжим за точку В и отложим BC = ОВ = R, то точки О, А, С и M будут вершинами параллелограмма.

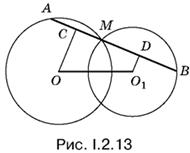
2.13. Пусть через точку M пересечения двух окружностей с центрами О и О₁ (рис. I.2.13) проведена секущая AB данной длины. Проведем к ней перпендикуляры ОС и О₁D. Отрезок CD вдвое меньше отрезка AB, так как точки С и D — соответственно середины хорд AM и МВ.

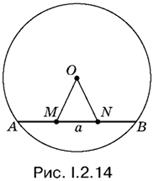
2.14. Если хорда AB искомая, то МВ − AM = а. Построим отрезок BN, равный AM (рис. I.2.14). Точки M и N лежат на одинаковом расстоянии от точки О, а MN = а.

2.15. Так как длина отрезка PQ и несущая его прямая известны, то можно воспользоваться методом параллельного переноса.

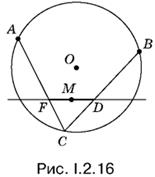
2.16. Нужно построить отрезок FD (рис. I.2.16), делящийся в точке M пополам. Следовательно, его можно рассматривать как одну из диагоналей параллелограмма. В качестве одной из вершин параллелограмма удобно выбрать точку В. Отразив ее симметрично от точки M, получим еще одну вершину.

2.17. Если через точки А и В провести прямую, то она, вообще говоря, должна пересечь прямую PQ в некоторой точке С. Остается воспользоваться свойством секущей и касательной, проходящих через общую точку. Случай, когда AB и PQ параллельны, рассмотрите отдельно. (!)

2.18. Соединить точку M с концами А и В данного диаметра. Рассмотреть получившиеся точки пересечения с окружностью.

2.19. Воспользоваться предыдущей задачей и построить произвольный перпендикуляр к данному диаметру, пересекающий окружность в точках С и D.

2.20. Какую бы точку С на прямой l мы ни взяли, величина |AC − BC| в силу неравенства треугольника не может превзойти длины отрезка AB. Следовательно, существует точка прямой l, отвечающая требованиям задачи. По условию точки А и В лежат по разные стороны прямой l. Принципиально ли это требование, или же можно сформулировать эквивалентную задачу для точек, лежащих по одну сторону прямой l?

2.21. Для построения естественно воспользоваться обычным методом геометрических мест. Каждая вершина квадрата лежит на внешней половине окружности, построенной на стороне четырехугольника как на диаметре. Чтобы отыскать второе геометрическое место точек, которому принадлежат вершины, нужно выяснить, что связана какая-то из линий, определяющих вершины, с данным четырехугольником. Рассмотрите с этой целью диагональ квадрата.

2.22. Дан отрезок и известно, что его длина 7. Отрезок длины 1 не известен. Если бы он был дан, то отрезок длины √7 можно построить, как только мы построим отрезок длины √3. Затем построим гипотенузу прямоугольного треугольника со сторонами √3 и 2.

2.23. Решение можно искать только при одновременном выполнении условий:

K главе 3

3.1. Чтобы связать участвующие в задаче элементы, нужно отрезок ОА луча, перпендикулярного к ребру, спроецировать на другую полуплоскость. Проекцию ОВ этого отрезка спроецировать в отрезок ОС, лежащий на втором луче.

3.2. Чтобы связать данные углы с величиной угла, который нужно найти, следует спроецировать катеты треугольника на плоскость P и построить искомый угол.

3.3. При проецировании угла α на плоскость P возникает четырехгранный угол, в котором три плоских угла даны, а два двугранных угла прямые. Чтобы установить связь между плоскими углами, нужно пересечь этот четырехгранный угол плоскостью Q, перпендикулярной к плоскости P.

3.4. Если спроецировать искомую прямую, параллельную а, на плоскость, перпендикулярную к а, то мы получим точку. Спроецируйте на эту же плоскость три оставшиеся прямые.

3.5. Начать нужно с построения искомого угла. Для этого прямые AB и SC нужно перенести в одну точку. Если сместить прямую SC, то она «повиснет в воздухе» и угол, который мы получим, не будет связан с треугольником. Поэтому проведем через току C прямую CD, параллельную AB; угол SCD искомый.

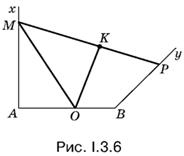
3.6. Лучи Аx и Вy удобно расположить так, как показано на рис. I.3.6. Утверждение, что ОК = АО, равносильно утверждению, что АM = MK (рассмотрите прямоугольные треугольники ОАМ и OKM).

3.7. Если такое сечение четырехгранного угла существует, то в результате параллельного сдвига плоскости этого сечения мы получим новую плоскость, пересечение которой с четырехгранным углом — тоже параллелограмм. Поэтому строить сечение можно в любой точке ребра четырехгранного угла.

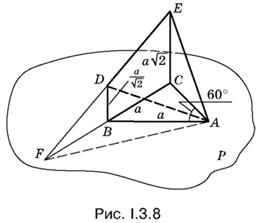
3.8. Если продолжить DE и BC до пересечения в точке F, то BD — средняя линия в треугольнике EFC (рис. I.3.8). Площадь треугольника DEА равна половине площади треугольника FEA.

3.9. Чтобы ответить на вопрос задачи, нужно определить высоту H пирамиды. Каждый из данных двугранных углов можно измерить с помощью линейного угла, опирающегося на высоту H. Остается использовать тот факт, что в основании лежит правильный треугольник.

3.10. Докажите, что высота, проведенная в треугольнике АDВ через вершину D, проходит через середину E основания AB. Тогда интересующий нас двугранный угол измеряется линейным углом DEC.

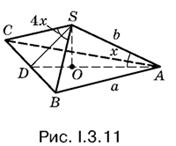
3.11. Условия задачи отражены на рис. I.3.11. Сторона а основания известна, так как известна площадь основания.

3.12. Аналогичное построение на плоскости приводит к образованию треугольника, подобного данному, с коэффициентом подобия ½. Поэтому и здесь следует постараться выяснить, подобны ли рассматриваемые тетраэдры.

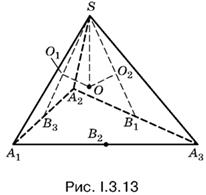
3.13. Если О — центр шара, касающегося боковых граней пирамиды в точках О₁, О₂ и О₃ (рис. I.3.13), то легко установить, что SB₁ = SB₂ = SB₃. Если мы сумеем доказать равенство треугольников А₂SВ₁ и А₂SВ₃, то установим, что в основании пирамиды лежит правильный треугольник.

3.14. Достроить усеченную пирамиду до полной и рассмотреть высоты пирамид, имеющих три основания, о которых идет речь в условии.

3.15. Построить угол между скрещивающимися прямыми можно, если параллельно перенести их так, чтобы они проходили через одну точку. В качестве такой точки удобно выбрать вершину А основания пирамиды. Если мы достроим треугольник АВС, лежащий в основании, до параллелограмма АВСЕ (рисунок сделайте самостоятельно), то угол DАЕ будет искомым. Образовавшаяся в результате четырехугольная пирамида будет состоять из ребер данной длины, за исключением ребра DЕ.

3.16. Тетраэдр разбивается на две пирамиды с общим основанием — плоскостью сечения. Данное отношение объемов позволяет найти отношение высот этих пирамид и, следовательно, отношение синусов искомых углов.

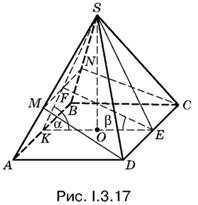
3.17. Условия задачи отражены на рис. I.3.17. Нас интересует отношение площадей треугольников DАМ и DМS, в то время как все известные элементы сосредоточены в плоскости KSЕ. Поэтому нужно связать элементы треугольников DАМ и DМS с элементами треугольника KSЕ.

3.18. Использовать условие задачи, согласно которому высота пирамиды, опущенная из вершины D, проходит через точку пересечения высот основания АВС, с тем, чтобы доказать, что треугольники АDВ и АDС прямоугольные.

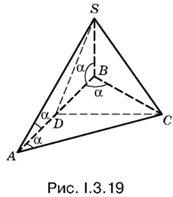
3.19. В пирамиде SАВС (рис. I.3.19) равнобедренные треугольники АSВ и АСВ равны. Следовательно, проведенные в них высоты из вершин S и С упадут в точку D — середину AB.

3.20. Если верхний из двух равных треугольников, лежащих один на другом в плоскости, начать вращать вокруг из общей стороны, то образованный ими двугранный угол может быть как острым, так и тупым. Поэтому придется рассмотреть два случая.

3.21. Если в основании АВС пирамиды провести высоту ВD, то отрезок SD разделит угол АSС пополам.

3.22. Покажите, что отрезки AB и CD взаимно перпендикулярны. Центр описанного шара лежит на их общем перпендикуляре KM, где K — середина СD, M — середина AB.

3.23. Расстояние от основания высоты до бокового ребра измеряется отрезком перпендикуляра, опущенного на боковое ребро. Чтобы связать участвующие в задаче величины, нужно измерить двугранный угол α линейным углом, построенным в точке бокового ребра, которая является основанием этого перпендикуляра. Следовательно, придется построить сечение пирамиды, проходящее через основание высоты и перпендикулярное к боковому ребру пирамиды.

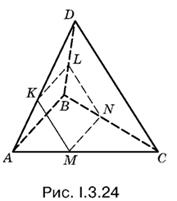
3.24. Чтобы в сечении получился квадрат, плоскость сечения необходимо провести так, чтобы она пересекала все четыре грани пирамиды (иначе мы получили бы в сечении треугольник). Докажите, что если KLNM — квадрат (рис. I.3.24), то плоскость KLNM параллельна двум скрещивающимся прямым AB и СD.

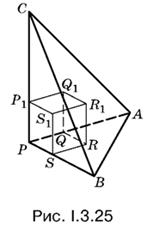
3.25. Для того чтобы найти наиболее рациональное решение задачи, поставьте пирамиду на одну из боковых граней (рис. I.3.25), а затем примените сравнение объемов.

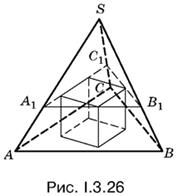
3.26. Вписать в пирамиду куб значит расположить его так, чтобы нижнее основание куба лежало на основании пирамиды, а верхнее основание куба было вписано в треугольник, полученный в горизонтальном сечении пирамиды (рис. I.3.26).

3.27. K решению этой задачи удобно подойти аналитически, рассмотрев общий случай. Предположим, что в сечении образовался некоторый треугольник со сторонами а, b и с. Полезно рассмотреть пирамиду, в основании которой лежит этот треугольник, а вершиной является вершина трехгранного угла.

3.28. По условию задачи попарно равны именно те ребра тетраэдра, которые лежат на скрещивающихся прямых. Использовать это условие можно, если расположить тетраэдр так, чтобы ребро AB лежало в горизонтальной плоскости P, а ребро DС было параллельно этой плоскости.

3.29. Нужно построить расстояние между прямыми AB и CD. Для этого через один из отрезков, например через AB, надо провести плоскость P, параллельную CD.

Решение естественно начать с построения плоскости P, проходящей через одно ребро (AB) и параллельной другому (CD). Удобный чертеж можно получить, повернув пирамиду вокруг AB так, чтобы плоскость P стала горизонтальной.

Далее нужно построить угол между скрещивающимися прямыми AB и CD. Напомним, что для этого достаточно построить прямую, пересекающую одну из них и параллельную другой.

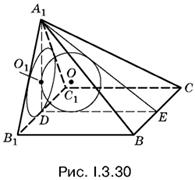
3.30. Плоскость А₁ВС отсекает от призмы четырехугольную пирамиду. Расположим ее так, как показано на рис. I.3.30. То, что в эту пирамиду вписан шар радиусом R, означает, что в треугольники В₁А₁С₁ и DА₁Е вписаны окружности радиусом R.

3.31. В силу соображений симметрии центр шара, о котором идет речь в задаче, совпадает с центром шара, вписанного в правильный тетраэдр.

3.32. Если куб преобразовать подобно, выбрав в качестве центра подобия точку О, то диагональ, проходящая через точку О, сохранит свое направление в пространстве.

3.33. Составным элементом этой задачи является соотношение, связывающее разность углов треугольника, прилегающих к некоторой его стороне, с углом между этой стороной и биссектрисой противоположного угла.

3.34. Диагонали, расстояние между которыми нужно найти, будут лежать на скрещивающихся прямых. Расстояние между скрещивающимися прямыми равно расстоянию между определяемыми ими параллельными плоскостями.

3.35. Так как сфера с центром в точке О расположена симметрично относительно всех трех ребер, выходящих из А, то О должна лежать на диагонали куба.

3.36. Вначале нужно извлечь информацию из того обстоятельства, что проекции каждой стороны четырехугольника на взаимно перпендикулярные плоскости равны. Отсюда следует, что каждая сторона четырехугольника параллельна плоскости, делящей угол между взаимно перпендикулярными плоскостями пополам.

3.37. Задачу можно свести к такой: доказать, что объем конуса меньше куба его образующей. (!)

3.38. Введите линейные элементы, характеризующие конус, например высоту H и радиус основания ρ. Затем величины H, ρ и p выразите через радиусы R и r шаров.

3.39. Чтобы использовать данное в условии отношение объемов двух конусов, нужно выразить радиус основания одного конуса через радиус основания другого. Для этого придется внутренний конус, свободно вращающийся в шаре, закрепить так, чтобы образующие конусов были параллельны.

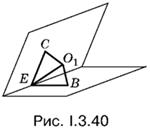
3.40. Не следует начинать решение с построения общего чертежа, который окажется весьма громоздким. Удобнее вначале провести анализ условия и вспомнить, что центр сферы, вписанной в двугранный угол (рис. I.3.40), лежит в плоскости, проходящей через точки касания В и С и перпендикулярной к ребру этого угла. Линейный угол ВЕС делится прямой EO₁ пополам, а отрезки СЕ и ВЕ равны. Если сделать соответствующие построения для треугольной пирамиды, то появится возможность использовать условие, что данная пирамида правильная.

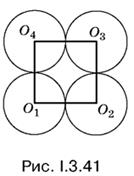
3.41. Центры четырех шаров, касающихся основания конуса, лежат в одной плоскости (рис. I.3.41). Если мы проведем осевое сечение конуса через O₁ и О₃, то сможем связать высоту H и радиус основания R конуса с радиусом r.

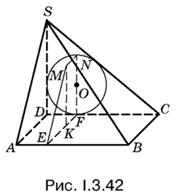
3.42. Необходимые построения показаны на рис. I.3.42. Плоскость EMNF проходит через ось цилиндра и перпендикулярна к основанию пирамиды; F — точка касания окружности основания цилиндра со стороной DС; M — точка касания с гранью ASB. Отрезки МК и EF взаимно перпендикулярны, KF — искомая величина.

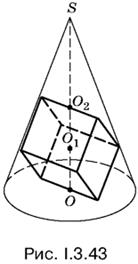
3.43. Условия задачи отражены на рис. I.3.43. Ввести линейные элементы, определяющие конус, и выразить их через ребро куба.

3.44. Поскольку в усеченную пирамиду вписан шар, то объем пирамиды можно представить в виде произведения одной трети радиуса шара на полную поверхность пирамиды. Обозначим стороны нижнего и верхнего основания через а и b соответственно. Воспользовавшись сравнением объемов, — в качестве второго выражения для объема нужно взять обычную формулу

— выразим площадь боковой грани пирамиды через а и b.

3.45. Нет необходимости изображать сами шары. Достаточно изобразить их центры и точки их касания с плоскостью.

3.46. Фигуры, о которых говорится в условии задачи, расположены так, что у них имеются две плоскости симметрии. Первая плоскость симметрии пройдет через ребро данного двугранного угла и через центр меньшего шара. На этой плоскости окажутся центры двух других шаров. Вторая плоскость симметрии будет перпендикулярна к ребру двугранного угла и тоже пройдет через центр меньшего шара. Поэтому достаточно сделать каркасный чертеж, на котором изобразить лишь одну из четырех равных частей данной конфигурации.

3.47. У рассматриваемой фигуры будут три плоскости симметрии, проходящие через ось конуса и центр одного из шаров. Проекции центров трех шаров на плоскость P образуют равносторонний треугольник, сторона которого равна 2R. Сделать каркасный чертеж.

3.48. Чтобы использовать условие задачи, нужно рассмотреть два соседних конуса. При этом нет необходимости рисовать их целиком, достаточно изобразить оси, общую образующую и образующие, по которым конусы касаются плоскости.

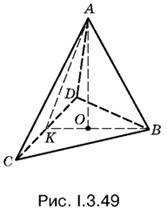
3.49. По условию сфера, радиус которой нужно найти, вписана в трехгранный угол А (рис. I.3.49). Это означает, что ее центр лежит на высоте АО. Однако все точки высоты АО (кроме концов) лежат внутри сферы, построенной на AB. Следовательно, касание двух сфер может быть только внутренним.

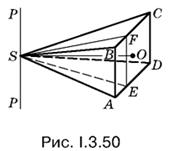
3.50. Искомое тело можно представить себе как часть пространства, заполненную в результате вращения вокруг оси РР (рис. I.3.50) треугольника SАВ и всех сечений пирамиды, проходящих через вершину S параллельно AB. Таким сечением является, например, треугольник SEF, изображенный на рис. I.3.50.

3.51. Способ 1. Задачу можно решить аналитически, если выразить полную поверхность конуса через радиус вписанного в него шара и угол а (рис. I.3.51; на нем изображено осевое сечение конуса). Затем следует воспользоваться соотношением S_пк = 2S_ш. В результате получим тригонометрическое уравнение относительно α.

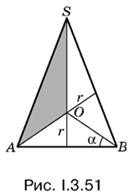
Способ 2. Объем конуса можно представить себе как сумму объемов V₁ и V₂ где V₁ — объем тела, полученного вращением треугольника ASO вокруг оси конуса, а V₂ — объем конуса с осевым сечением АОВ.

3.52. Пусть АВС и А₁В₁С₁ — основания призмы, а В₁В — ее ребро, принадлежащее двум равновеликим граням. Докажите, что вершина В₁ проецируется тогда на биссектрису одного из углов, образованных прямыми AB и BC. Может ли проекция вершины В₁ оказаться на биссектрисе внешнего угла треугольника АВС?

3.53. О пирамидах не сказано, какие они. Поэтому следует попытаться заполнить ими весь объем куба.

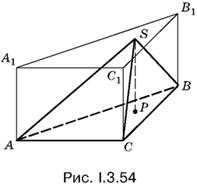
3.54. Высота SP пирамиды SABС (рис. I.3.54) фиксирована и равна 4. В основании правильный треугольник АВС со стороной 6. Кроме того, основание высоты не покидает треугольник АВС. Следовательно, вершина S пирамиды SАВС лежит в плоскости, параллельной плоскости треугольника АВС, и отстоящей от нее на расстоянии, равном 4. Если мы построим на основании АВС прямую призму А₁В₁С₁ABC с ребром 4, то вершина S пирамиды SАВС будет принадлежать верхнему основанию этой призмы.

K главе 4

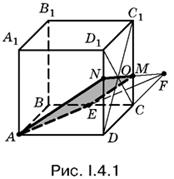
4.1. Построение сечения, о котором идет речь в задаче, показано на рис. I.4.1. Вначале найдена точка F сечения, лежащая в плоскости нижнего основания на пересечении прямых АЕ и DС.

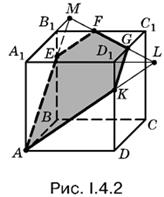
4.2. Построение сечения показано на рис. I.4.2, который подсказывает и рациональный способ вычисления площади сечения.

4.3. Чтобы построить сечение, проведите прямую через вершину А и центр верхнего основания и найдите точку пересечения этой прямой с ребром СС₁.

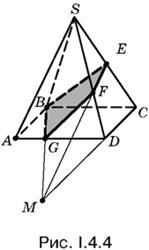
4.4. Сечение BEFG (рис. I.4.4) разбивает пирамиду на две части. Удобнее найти объем той части пирамиды, которая лежит под сечением, представив эту фигуру в виде разности двух пирамид EBCM и FGDM.

4.5. Сечение должно пройти через точки А, D и N (рис. I.4.5). Если их соединить, то получим пирамиду NACD, которую сечение отрезает от половины данной пирамиды.

4.6. Основную трудность в этой задаче представляет построение сечения. Начните с построения вспомогательного треугольника PQR.

4.7. Связать сечение с перпендикулярной к нему плоскостью центрального сечения пирамиды.

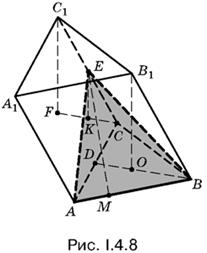
4.8. Чтобы вычислить площадь треугольника ABE, достаточно найти его высоту ЕМ (рис. I.4.8). Высоту B₁O призмы нетрудно вычислить, а высота EK пирамиды EABC в два раза меньше B₁O.

4.9. Чтобы построить сечение, достаточно провести через точку F два отрезка, лежащих внутри данного параллелепипеда: один в одной диагональной плоскости параллельно BD, а второй в другой диагональной плоскости параллельно AC₁.

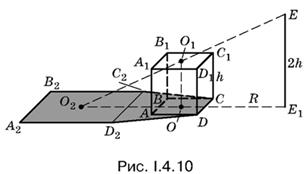
4.10. Построение тени, отбрасываемой кубом, показано на рис. I.4.10. Посмотрите, как будет изменяться тень при вращении источника света.

4.11. Площадь тени не изменится при произвольном параллельном переносе куба. Поэтому удобно расположить куб так, чтобы по крайней мере одна из его вершин (обозначим ее А) лежала в плоскости Π (рис. I.4.11).

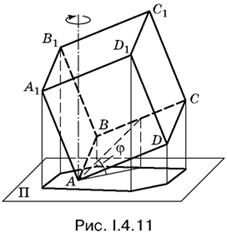
Площадь тени не изменится также и при вращении куба вокруг вертикальной прямой, проходящей через вершину А. Следовательно, для определения положения куба удобно воспользоваться острым углом между плоскостью его нижнего основания и плоскостью Π, который при таком вращении не изменяется.

Задача существенно упростится, если удастся выбрать в кубе простейшую фигуру, составленную из плоских фигур, которая отбрасывает на плоскость Π ту же самую тень.

K главе 5

5.1. Если точка M принадлежит геометрическому месту точек, то отрезок NО виден из нее под прямым углом. (!)

5.2. Если к треугольнику АМВ применить теорему косинусов, то получим еще одно соотношение, связывающее угол АМВ со сторонами треугольника.

5.3. Поскольку характеристики геометрического места точек содержатся в условии задачи, вполне удобно доказать, что любая точка окружности обладает указанным свойством. Для этого следует применить теорему косинусов к стороне МВ треугольника АМВ.

5.4. При любом выборе точки M треугольники АМВ и ВМС имеют общую сторону ВМ. Использовать условие равновеликости двух треугольников, имеющих общую сторону.

5.5. Пусть точка M зафиксирована. Площадь треугольника АВМ не изменится, если отрезок AB двигать по прямой AB. То же самое можно сказать о треугольнике СDМ. Остается рассмотреть два случая: 1) прямые AB и CD пересекаются, 2) прямые AB и CD параллельны.

5.6. Выясните, какую роль играет в задаче куб. Задачу можно разделить на две: вначале решить ту же задачу для прямых, на которых расположены диагонали куба, а затем высечь часть пространства, ограниченную кубом, и проследить, какие при этом произойдут изменения.

K главе 6

6.1. Воспользоваться тождеством p² − 1 = (p − 1)(p + 1).

6.2. Способ 1. Воспользоваться методом математической индукции. (!)

Способ 2. Разбить все числа на классы по модулю 3:

n = 3k, n = 3k + 1, n = 3k − 1,

и проверить утверждение для каждого класса. (!)

6.3. Поскольку 105 = 3 · 5 · 7, то а¹⁰⁵ = (а³)³⁵ = (а⁵)²¹ = (а⁷)¹⁵. Воспользуйтесь этим для разложения данного числа на множители.

6.4. Среди чисел от 1 до 500 будет 250 четных, 125 делящихся на 4 и т. д.

6.5. Чтобы данное число приняло более симметричный вид, его удобно умножить на 10. При этом делимость его на 81 не изменится.

6.6. Дополнить выражение n⁴ + 4 до полного квадрата и разложить на множители.

6.7. Так как по условию n четное, то нужно сделать подстановку n = 2k и привести данное выражение к общему знаменателю.

6.8. Способ 1. Дробь

сократима тогда и только тогда, если ее числитель представим в виде pr, а знаменатель — в виде qr, где p, q и r — целые числа и r ≠ ±1.

Способ 2. Если сократима дробь ^p/_q , то сократима и дробь ^q/_p.

6.9. Использовать сначала признак делимости на 4, а затем признак делимости на 9. (!)

6.10. Если условие, в силу которого число

в три раза меньше

записать символически, то получим уравнение, которое нужно будет решить в целых числах, каждое из которых расположено между 0 и 9.

6.11. Ясно, что число p нечетное. Одно значение p легко угадать — это p = 3. Есть ли другие?

6.12. Задачу удобнее решать от противного, исходя из предположения, что tg 5° = ^p/_q , где p и q — целые.

6.13. Если меньшее из чисел не оканчивается цифрой 9, то суммы цифр этих чисел различаются на 1. Поэтому обе суммы цифр одновременно делиться на 11 не могут. Нужно искать решение среди чисел, меньшее из которых оканчивается одной или несколькими цифрами 9.

6.14. Нужно правильно использовать условие, в силу которого x и у — целые. Однородное выражение относительно неизвестных нужно оставить слева и попытаться разложить на множители, а число 17 перенести в правую часть равенства.

6.15. Данное уравнение таково, что если x = а, у = b — его решение, то существуют еще три решения: (−а, b), (а, −b), (−а, −b), если а ≠ b.

6.16. Преобразовать исходное условие к виду 11(4x − 1) = 69(у − x) и воспользоваться тем, что x и у — натуральные числа.

K главе 7

7.1. Обе двойки представить как 3 − 1 и сгруппировать члены так, чтобы в числителе можно было вынести за скобки n + 1, а в знаменателе n − 1.

7.2. Прежде чем выполнять действия в скобках, следует упростить дроби, разложив числители и знаменатели на множители.

7.3. Перед нами сумма из трех слагаемых. Если первые два привести к общему знаменателю, то в числителе произойдут существенные упрощения.

7.4. Прежде чем производить вычитание, следует упростить дробь.

7.5. Если вынести за скобки х^2m, то в скобках останется x в степени, содержащей множителями m − n и ¹/_mn . Это упростит дальнейшие преобразования. (!)

7.6. Каждое из подкоренных выражений является полным квадратом.

7.7. Обратить внимание на то, что

9 + 4√2 = 8 + 4√2 + 1 = (2√2 + 1)².

7.8. Каждую из вторых скобок разбить на два слагаемых x² − u² и z² − у², после чего собрать все члены, содержащие множитель x² − u², и все члены, содержащие z² − у². (!)

7.9. Если обозначить левую часть через z, то, освобождаясь от радикалов, можно получить уравнение относительно z.

7.10. Равенство, которое нужно доказать, представляет собой однородное выражение седьмой степени. Возвести в степень

а + b + с = 0 и а + b = −с.

7.11. Задача сводится к разбору случаев, позволяющих раскрыть знаки абсолютной величины. Количество рассматриваемых случаев можно уменьшить, если заметить, что равенство, о котором идет речь, не меняется при замене x на −x.

7.12. Можно разобрать различные случаи взаимного расположения чисел x, у и 0. Однако проще возвести каждую часть в квадрат. Так как обе части неотрицательны, то мы получим равенство, равносильное данному. (!)

7.13. Условие можно записать в виде а^⅓ + b^⅓ = −с^⅓ и возвести это соотношение в куб.

7.14. Данный трехчлен тождественно равен выражению

(ax + b)³ − (сх + d)³, где а > 0, b > 0, с > 0, d > 0.

K главе 8

8.1. Поскольку выражения, стоящие в скобках, расположены симметрично относительно значения x = 5, удобно ввести новое неизвестное у = x − 5. После того как мы раскроем скобки, произойдут значительные упрощения. (!)

8.2. Можно перемножить скобки по две, чтобы получить квадратные трехчлены, отличающиеся только свободным членом.

8.3. Если записать уравнение в виде x² − 17 = 3у², то возникает мысль доказать, что левая часть ни при каких целых x не делится на 3. (!)

8.4. Если целое у зафиксировать, то получим квадратное уравнение относительно x. Поэтому естественно обратить внимание на те ограничения, которые накладывает на у условие неотрицательности дискриминанта этого уравнения. (!)

8.5. Остаток следует искать в виде аx + b, а частное удобно обозначить через Q(x). Следуя определению деления, записать тождество.

8.6. Если переписать уравнение в виде

то благодаря условию целочисленности решений можно ограничить возможные значения у рассмотрением нескольких случаев.

8.7. Если подставить известный корень в уравнение, найти коэффициенты при рациональной и иррациональной частях, то получим систему двух уравнений для определения а и b.

8.8. Ответьте на вопрос: достаточно ли воспользоваться теоремой Виета, в силу которой свободный член и второй коэффициент должны быть положительными?

8.9. Если обозначить первый корень через x₁, а знаменатель прогрессии через q, то останется применить теорему Виета. (!)

8.10. С помощью теоремы Виета получить зависимость между α₁, α₂, α₃ и коэффициентами данного уравнения. (!)

8.11. Разделить x³ + аx + 1 на x − α по правилу деления многочлена на двучлен.

8.12. Ясно, что остаток нужно искать в виде аx + b. Если данный многочлен обозначить через P(x), а частное от его деления на (x − 2)(x − 3) — через Q(x), то мы сможем воспользоваться определением деления многочленов.

8.13. Если многочлен x⁴ + 1 разделится на x² + рx + q, то в частном мы получим многочлен второй степени, т. е. x² + аx + b.

8.14. Если данный многочлен делится на (x − 1)³, то после замены x − 1 = у получим многочлен, который должен делиться на у³.

8.15. Если многочлен четвертой степени с коэффициентом 6 при старшем члене делится на x² − x + q без остатка, то в частном обязательно получится многочлен 6x² + аx + b, в котором а и b определяются одновременно с p и q.

K главе 9

9.1. Точки −2, −1, 0 делят числовую ось на четыре интервала, в каждом из которых нужно решить данное уравнение. (!)

9.2. Если рассматривать значения x, обращающие в нуль числа, стоящие под знаками абсолютных величин, то придется разбить числовую ось на пять частей.

Удобнее ввести новое неизвестное у = x². (!)

9.3. Это уравнение четвертой степени. Следовательно, нужно найти искусственный прием, приводящий к его решению. Удобно воспользоваться тем, что слева стоит сумма квадратов.

9.4. Возвести в куб и сравнить полученное уравнение с данным.

9.5. Свести уравнение к симметрической системе, обозначив первое слагаемое левой части через u, а второе через v. (!)

9.6. Если под радикалами раскрыть скобки, то получим квадратные трехчлены, отличающиеся лишь свободным членом. Поэтому данное в условии уравнение удобно заменить системой, обозначив первое слагаемое его левой части через u, а второе через v.

9.7. Поскольку неизвестное входит в уравнение либо в сочетании x − b, либо в сочетании а − x, то удобно ввести обозначения

и получить систему алгебраических уравнений.

9.8. Ввести вспомогательное неизвестное у и свести решение данного уравнения к решению системы уравнений относительно x и у.

9.9. Перенести

в правую часть уравнения и возвести обе части в квадрат.

9.10. Чтобы избавиться от знаков абсолютной величины, можно поступить двояко: либо потребовать, чтобы правая часть уравнения была неотрицательной, и решить уравнения

x² − ^3x/₂ − 1 = −x² − 4x + β, x² − ^3x/₂ − 1 = x² + 4x − β;

либо рассмотреть два случая: в первом выражение, стоящее под знаком абсолютной величины, неотрицательно, а во втором — отрицательно.

9.11. Рассмотреть различные случаи расположения x и у по отношению к нулю (всего придется рассмотреть четыре случая). (!)

9.12. Решить систему уравнений с параметром k, а затем решить систему неравенств. (!)

9.13. Рассмотреть различные случаи взаимного расположения чисел x и у и чисел x и −у. Это позволит раскрыть знаки абсолютной величины. (!)

9.14. Второе уравнение — уравнение окружности радиуса √а . Нарисовать кривую, которая определяется первым уравнением.

9.15. Одно решение очевидно: x = у = 0. Если ху ≠ 0, то можно разделить первое уравнение на ху, а второе на x²у².

9.16. Если бы во втором и третьем уравнениях не было коэффициентов 2 и 3, то уравнения системы получались бы друг из друга с помощью циклической перестановки неизвестных x, у и z. Однако влияние коэффициентов оказывается столь сильным, что попытка использовать это свойство системы не приводит к успеху. Попытайтесь преобразовать систему в распадающуюся, для чего потребуется отыскать алгебраическое выражение, общее для двух уравнений, и исключить его.

9.17. Если первое уравнение системы записать в виде x + у = −z и возвести в квадрат, то с помощью второго ее уравнения можно найти ху.

9.18. Сопоставьте первое и последнее уравнения. Если записать их в виде

x + у = 1 − z, х³ + у³ = 1 − z³,

то напрашивается способ, с помощью которого можно преобразовать систему в распадающуюся.

9.19. Если раскрыть скобки, то получим систему линейных уравнений относительно u = x + у + z, v = ху + xz + yz, w = xyz. Найдя u, v и w, можно вычислить х³ + у³ + z³, если возвести x + у + z = u в куб: u³ = х³ + у³ + z³ + 3uv − 3w.

Однако такой путь решения, хотя и прост по идее, требует значительных выкладок. Решение можно упростить, если ввести в рассмотрение многочлен M(t) = (t − x)(t − у)(t − z) + а, который в силу условия задачи имеет корни t = а, t = b, t = с.

9.20. Первые два уравнения системы симметричны относительно x и у. Нужно использовать эту симметрию для того, чтобы получить одинаковые правые части у этих двух уравнений.

9.21. Если второе уравнение возвести в квадрат, то можно сравнить два выражения для (x + у)². (!)

9.22. В первое уравнение входит у, в последующие уt, yt² и yt³ соответственно. Эта закономерность позволяет исключить у.

9.23. Каждый элемент, стоящий в левой части второго уравнения, получается из соответствующего элемента, стоящего в левой части первого уравнения, возведением в квадрат. Нужно использовать это свойство системы.

9.24. Левые части всех трех уравнений симметричны относительно x, у, z. Поэтому, подвергнув какому-то преобразованию любые два уравнения системы, разумно сделать то же самое и с оставшимися двумя парами уравнений.

9.25. Если известна сумма s = x₁ + x₂ + ... + x_n, то из каждого уравнения можно найти соответствующее x_k.

9.26. Чтобы избежать возведения двучлена в третью и, тем более, в пятую степень, нужно ввести новые неизвестные так, чтобы выражение 7x − 11у было одним из этих неизвестных.

9.27. Поскольку

входит в оба уравнения с разными знаками, а √у — с одинаковыми, то естественно сложить данные уравнения и вычесть. При этом мы приходим к системе, у которой слева стоят сумма и разность одинаковых радикалов, а справа — разные радикалы.

9.28. Чтобы левые части уравнений стали однородными относительно неизвестных, удобно ввести новое неизвестное z = √у.

9.29. Если каждое из уравнений возвести в квадрат, то получим систему относительно u = x² и v = у². Проверка здесь может оказаться довольно сложной, поэтому целесообразно следить за равносильностью в процессе решения. Чтобы в результате возведения в квадрат не появились посторонние решения, достаточно записать ограничения: x > 0, у > 0.

9.30. Все члены системы, содержащие x и у, однородны второй степени относительно x и у. Пусть данная система имеет решения x₁, у₁, z₁ Укажите симметричное решение, которое наряду с этим будет иметь система.

9.31. Поскольку вместе с условием x + у = 0 мы получаем три уравнения с двумя неизвестными, то имеет смысл воспользоваться подстановкой у = −x.

9.32. Поскольку данная система должна иметь решение при любом b, то, чтобы сузить область допустимых значений а, можно рассмотреть эту систему при некотором фиксированном b.

9.33. Вначале нужно использовать условие, что система должна иметь только одно решение. Второе уравнение можно рассматривать как четную функцию относительно x и у, т. е. наряду с решением x = x₁, у = у₁ оно имеет три симметричных решения: (−x₁, у₁), (x₁, −у₁), (−x₁, −у₁). Какое из этих решений наряду с (x₁, у₁) будет удовлетворять первому уравнению?

9.34. Второе уравнение можно преобразовать к виду

умножив числитель и знаменатель дроби на выражение, сопряженное знаменателю. Легко убедиться, что у ≠ 0. Поэтому можно полученное уравнение разделить на у, после чего нетрудно с помощью первого уравнения системы исключить

9.35. Представить уравнение в виде

|6 − |x − 3| − |x + 1|| = а(x + 5) + 4,

построить график функции, стоящей в левой части равенства, и рассмотреть поведение относительно этого графика прямой у = а(x + 5) + 4 при разных значениях а.

9.36. Обе части нужно возвести в квадрат. Чтобы обеспечить равносильность, в системе с полученным уравнением придется решать неравенство 4x² − 3аx ≥ 0. При этом выражение под вторым радикалом автоматически будет неотрицательным.

В задачах с параметрами, как правило, нарушать равносильность нецелесообразно. Рассуждения, связанные с ОДЗ, не дают строгого решения.

9.37. x = 0 — корень уравнения. Выражения в знаменателях имеют одинаковую составляющую 5x² + 6.

9.38. Это система однородных уравнений, и она решается стандартной подстановкой x + у = u, xу = v.

K главе 10

10.1. Из условия а + b = 2 следует, что числа а и b расположены симметрично относительно единицы. Использовать этот факт.

10.2. Условие а₁а₂...а_n = 1 можно использовать при преобразовании левой части неравенства, умножая или деля ее на произведение а₁а₂...а_n. Поскольку число множителей 1 + а_i совпадает с показателем степени в правой части неравенства и все множители равноправны, то следует доказать, что каждый из них не меньше двух.

10.3. Способ 1. Поделить данное в условии равенство а + b = с почленно на с^⅓.

Способ 2. Доказать эквивалентное неравенство:

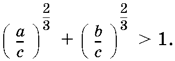
10.4. Избавиться от дробей и использовать условие 0 ≤ x ≤ 1. Это условие обеспечивает выполнение таких неравенств, как x^{k + 1} ≤ x^k, 1 − x^k ≥ 0 при любом натуральном k. (!)

10.5. Оценить каждый корень с помощью неравенства между средним геометрическим и средним арифметическим двух чисел, взяв в качестве первого числа подкоренное выражение, а в качестве второго единицу.

10.6. Предположить, что b ≤ а, и оценить левую часть данного неравенства, заменив b на а. (!)

10.7. Если бы между правой и левой частями стоял знак равенства, то мы имели бы производную пропорцию от

10.8. Воспользоваться неравенством между средним арифметическим и средним геометрическим двух чисел.

10.9. Способ 1. Если обозначить три положительных слагаемых в левой части неравенства через u, v и w, то uvw = 1. Следовательно, среди чисел u, v и w есть одно большее единицы и одно меньшее единицы, например, u > 1, v < 1. Тогда (1 − u)(v − 1) > 0.

Способ 2. Если u, v и w — положительные числа, причем w — наименьшее, то u > w, v > w. Неравенство v > w можно умножить на положительное число u − w и полученное неравенство разделить почленно на uw.

Способ 3. Если с < b < а, то можно записать, что b = с + d₁, а = b + d₂, где d₁ и d₂ — положительные числа. Подставьте в левую часть неравенства вместо а и b их выражения с + d₁ и b + d₂— соответственно.

10.10. Преобразования удобно начать с записи S по формуле Герона. Величину S нужно оценить так, чтобы прийти к выражению, симметричному относительно а, b и с. Поскольку из четырех множителей p, p − а, p − b, p − с первый удовлетворяет этому требованию (2р = а + b + с), следует подвергнуть преобразованиям три других множителя. При этом полезно обратить внимание на то обстоятельство, что их сумма равна p:

p − а + p − b + p − с = 3р − (а + b + с) = p.

10.11. Если перемножить крайние и средние скобки, то получатся два трехчлена, отличающиеся только свободным членом. Это позволяет оценить левую часть, выделив квадрат трехчлена, свободный член которого находится посередине между свободными членами первого и второго трехчленов. (!)

10.12. Данные уравнения симметричны относительно у и z и не симметричны (второе) относительно x. Если воспользоваться вторым уравнением и из первого выразить у + z через x, то мы получим простую систему относительно у и z, где x выступает в роли свободного члена.

10.13. Данные уравнения можно переписать в виде

у + z = 5 − x, yz + x(z + y) = 8,

после чего можно получить уравнение, корнями которого будут у и z, а коэффициенты будут зависеть от x.

10.14. Нужно рассмотреть три случая, в зависимости от того, положителен, отрицателен или равен нулю дискриминант трехчлена. Затем обратить внимание на знак старшего коэффициента. (!)

10.15. Так как коэффициент при x² положителен, то ветви параболы направлены вверх. Рассмотреть возможное расположение корней параболы относительно отрезка 1 < x < 2.

10.16. Воспользоваться теоремой Виета и рассмотреть случаи, когда х₁ и x₂ одного знака и разных знаков.

10.17. Определить направление ветвей параболы и расположение ее корней относительно точек −1 и +1, чтобы условия задачи выполнялись.

10.18. Если m ≠ 0 (случай m = 0 следует рассмотреть отдельно), то ветви параболы у = mx² − 4x + 3m + 1 должны быть направлены вверх.

10.19. Рассмотреть случаи, позволяющие раскрыть знаки абсолютной величины. Удобнее записать это неравенство как совокупность двух систем: в первой выражение, стоящее под знаком абсолютной величины, неотрицательно, а во второй системе оно отрицательно. (!)

10.20. Чтобы избавиться от знаков абсолютных величин, достаточно вспомнить о том, как они могли быть получены, например

= |x − 3|. (!)

10.21. Чтобы упростить данное неравенство, его нужно умножить на 4x. Поскольку результат будет зависеть от знака x, необходимо рассмотреть два случая: x < 0 и x > 0. (!)

10.22. Если перенести 3 в левую часть неравенства и привести полученное выражение к общему знаменателю, то получим дробь, которая должна быть отрицательной.

10.23. Неравенство можно упростить, если перенести все в одну сторону, привести выражения, стоящие под радикалами, к общему знаменателю и вынести за скобки неотрицательный множитель

10.24. Удобно рассмотреть два случая: x > 0 и x < 0 (при x = 0 сразу видно, что неравенство не выполняется).

10.25. В неравенство входит сумма двух выражений: √x ,

— и их удвоенное произведение. Кроме этого, в правой части стоит член −2x, который после перенесения его в левую часть можно использовать для образования суммы квадратов этих выражений.

10.26. Поскольку второе слагаемое всегда неотрицательно, целесообразно рассмотреть два случая: x > 0 и x ≤ 0.

10.27. Если привести обе части неравенства к основанию 2, то можно заметить симметрию показателей.

10.28. Если перенести все влево и сгруппировать члены, содержащие иррациональное выражение в показателе степени, то это поможет разложить левую часть на множители. (!)

10.29. Придется разобрать два случая: x > 0 и x ≤ 0. Когда x > 0, данное неравенство равносильно такому:

10.30. Чтобы сравнить показатели степени, необходимо выяснить, как основание расположено по отношению к единице.

10.31. Так как обязательно x > 0, то можно упростить неравенство, разделив обе его части на x.

10.32. При x > 0 получаем равносильное неравенство

Что будет при x < 0?

10.33. При возведении в квадрат нужно потребовать, чтобы подкоренное выражение было неотрицательным. (!)

10.34. Выражение, стоящее под знаком логарифма, должно быть положительным. Абсолютная величина выражения неотрицательна. Как видите, это не совсем одно и то же. (!)

10.35. При решении логарифмических неравенств удобнее иметь дело с одинаковыми основаниями логарифмов. Если вы выбрали в качестве такого основания число 5, то обратите внимание на правую часть неравенства. Осуществив в ней почленное деление числителя на знаменатель, вы обнаружите, что

При этом появляются ограничения x > 0, x ≠ 1. Существенны ли они в процессе решения?

10.36. Перейти к одному основанию и получить под знаками логарифма одинаковое число. (!)

10.37. Неравенство легко приводится к виду

log_{|x + 6|}(x² − x − 2) ≥ 1. (!)

10.38. Если обозначить log_аx = у, то получим простое неравенство относительно у.

10.39. Перейти к общему основанию k.

10.40. Вообще говоря, нужно рассмотреть случаи, когда основание x больше единицы и когда оно находится между нулем и единицей. Однако внимательное изучение данного неравенства позволяет рассмотреть только один из этих случаев.

10.41. Поскольку основание логарифма больше единицы, данное неравенство эквивалентно требованию, чтобы число, стоящее под знаком логарифма, было не меньше единицы.

10.42. Чтобы упростить это неравенство, нужно рассмотреть два случая, в зависимости от того, больше или меньше единицы основание логарифма. Однако правильное использование условия позволяет исключить случай

0 < (x − 1)² < 1.

10.43. Полезно обратить внимание на то обстоятельство, что первый сомножитель положителен. Следовательно, и второй сомножитель тоже должен быть больше нуля.

10.44. Нужно начать с приведения логарифмов к основаниям 2 и 3.

10.45. Поскольку неизвестно, как расположено выражение, стоящее в основании логарифма, относительно 1, то придется рассмотреть два случая: 0 < x² − 1 < 1 и x² − 1 > 1. (!)

10.46. Поскольку мы ищем как решения, при которых основание положительно, так и решения, при которых оно отрицательно, удобно начать с определения тех интервалов изменения x, где основание сохраняет свой знак.

10.47. Если у ≠ 0 фиксировано, то данное неравенство является обычным квадратным неравенством относительно x. Остается записать условие, при котором это квадратное неравенство имеет решение.

10.48. Прежде чем приступить к «техническому» решению задачи, ответьте на вопрос, следует ли из неравенства 3 < 2, например, теорема синусов?

10.49. Чтобы составить план решения, нужно рассмотреть строгое неравенство:

Корень в левой части этого неравенства существует и положителен при x < а. Поэтому оно равносильно системе

10.50. Разложить оба квадратных трехчлена на множители и общий множитель вынести за скобки.

10.51. Откажитесь от идеи непосредственной проверки данных в условии чисел путем их подстановки в неравенство. Проще это неравенство решить. (!)

10.52. Обратите внимание, что числа √5 + 2 и √5 − 2 при перемножении дают 1, т. е. эти числа взаимно обратны.

10.53. Обозначив log₂x = у, можно привести неравенство к виду

1 + у² ≤ |у| (4x − x² − 2).

В выражении в скобках нужно выделить полный квадрат.

K главе 11

11.1. С помощью формулы перехода к другому основанию можно выразить искомое число через десятичные логарифмы.

11.2. Число 1225 нужно разложить на простые множители. (!)

11.3. Перенести степени с основанием 2 в правую часть уравнения, а с основанием 3 в левую. После преобразований уравнения его правая часть может быть записана как 2 в некоторой степени, а левая — как степень числа 3.

11.4. Обозначить 3^{−|x − 2|} = у и исследовать квадратное уравнение.

11.5. Обозначить 12^|x| = у. При исследовании учесть, что не только дискриминант не должен быть отрицательным, но и найденные значения у не могут стать меньше 1. (!)

11.6. Уравнение можно переписать в виде

Прежде чем прологарифмировать, удобно получить в правой части единицу. (!)

11.7. Использовать тот факт, что числа 2 + √3 и 2 − √З взаимно обратные

11.8. Уравнение примет более симметричный вид, если разделить обе его части на 2^x.

11.9. Отдельно рассмотреть случаи, когда основание равно 0, 1, −1. (!)

11.10. Привести к одинаковому числу под знаком логарифма.

11.11. С помощью формулы log_ab = log_a^k b^k можно добиться того, что в уравнение будут входить только log_x7 и log₇x.

11.12. Если уравнение прологарифмировать по основанию 3, то мы получим уравнение третьей степени относительно log₃x. (!)

11.13. Уравнение легко преобразовать в иррациональное с помощью замены у = log_x 3. (!)

11.14. Так как 2 log_x 2 = log_x 4, то после умножения обеих частей уравнения на log₄x оно упростится. Нарушится ли при этом равносильность?

11.15. Вид уравнения подсказывает, что для его решения удобно перейти к логарифмам с общим основанием x. Равносильное ли получится уравнение?

11.16. В уравнение входят логарифмы выражения 3 + x при разных основаниях. Его можно упростить, если воспользоваться формулой

11.17. При решении удобнее следить за равносильностью, чем делать в конце проверку, которая окажется здесь достаточно громоздкой.

11.18. Если log_√bx записать при основании а, то уравнение упростится.

11.19. Если в каждом из подкоренных выражений произвести логарифмирование с переходом к общему основанию а, то это позволит выделить под радикалами полные квадраты. Очевидно, такие же ограничения, как на а, должны быть наложены и на x.

11.20. Система не может иметь решений, в которых хотя бы одно неизвестное обращается в нуль (докажите). Следовательно, каждое уравнение можно прологарифмировать.

11.21. Поскольку нам известно, чему равно x^у, то второе уравнение целесообразно возвести в степень у.

11.22. Из вида системы следует, что x и у положительны. Так как в левых частях уравнений одинаковые показатели степени, то целесообразно попытаться их найти.

11.23. Так как 11^xz : 11^z = 11^{(x − 1)z}, то с помощью этого соотношения можно получить уравнение относительно

.

11.24. Так как коэффициенты в левых частях уравнений одинаковы (двойку во втором уравнении можно убрать, прибавив единицу к показателю степени), то целесообразно посмотреть, нет ли у левых частей общего множителя.

11.25. Вначале нужно перейти к общему основанию у логарифмов, а затем получить систему двух алгебраических уравнений.

11.26. Способ 1. Систему можно решить подстановкой, выразив из второго уравнения у через x.

Способ 2. Воспользоваться равенством а^log_b^c = с^log_b^а .

11.27. Решение системы нужно начать с использования ограничений, что позволит сократить число рассматриваемых случаев.

Из второго уравнения следует, что x и у — величины одного знака. Поскольку должен существовать log₂ (x + у), то x и у положительны. Сумму x + у легко сравнить с единицей.

11.28. Это — алгебраическая система относительно u = log₂x и v = log₂(у + 1). (!)

11.29. Оба уравнения можно упростить с помощью формулы

log_a^kN = ¹/_k log_aN (а > 0, а ≠ 1).

11.30. Первые два уравнения можно рассматривать как систему относительно соответствующих степеней тройки. Нетрудно заметить, что это позволит найти x.

K главе 12

12.1. Выражения, стоящие в квадратных скобках, существенно упростятся, если раскрыть скобки и выполнить возведение в степень. (!)

12.2. Это тождество по структуре похоже на формулу тангенса суммы. Чтобы заметить это, достаточно переписать его так:

tg 2α [tg (30° − α) + tg (60° − α)] = 1 − tg (60° − α) tg (30° − α).

12.3. Перенести ctg x в левую часть и преобразовать вместе с ½ tg ^x/₂.

12.4. Поскольку нам нужно получить соотношение, в котором участвуют α + β и α, то вместо sin β удобно записать sin [(α + β) − α] и воспользоваться формулой синуса разности. (!)

12.5. Домножить и разделить на 2 sin ^π/₇ и воспользоваться формулой синуса двойного угла. (!)

12.6. Вычислить произведение косинусов этих углов можно, если домножить и разделить его на 2 sin ^π/₇. После этого нужно трижды последовательно воспользоваться формулой синуса двойного угла (см. задачу 12.5).

12.7. Удобнее доказать, что правая часть равна левой. Для этого стоящее в правой части выражение нужно преобразовать с учетом данных равенств.

12.8. В произведении sin (x + у) sin (x − у) удобно раскрыть синус суммы и синус разности.

12.9. Выразить дробь, стоящую в правой части последнего равенства, через синусы и косинусы α и β.

12.10. Данное выражение и выражение, которое нужно вычислить, симметричны относительно α, β и γ. Левую часть данного равенства удобно выразить через sin²α, sin²β, sin²γ.

12.11. Подставить β = α + ^π/₃, γ = α + ^2π/₃ и записать данное выражение через синусы и косинусы.

12.12. Так как ctg α, ctg β и ctg γ образуют арифметическую прогрессию, то ctg α + ctg γ = 2 ctg β. Если теперь вспомнить, что β = ^π/₂ − (α + γ), то можно получить соотношение, не зависящее от ctg α + ctg γ. (!)

12.13. cos 106° = cos (90° + 16°) = −sin 16° = −2 sin 8° cos 8°.

K главе 13

13.1. Множитель √2 sin (x + ^π/₄) замените на sin x + cos x.

13.2. Левую часть можно преобразовать так, чтобы она содержала множителем выражение, стоящее в правой части.

13.3. Выразить левую часть уравнения через sin x и cos x так, чтобы оказалось возможным разложение ее на множители.

13.4. Если преобразовать в сумму произведение синусов двух функций и произведение косинусов этих же функций, то получим сопряженные выражения. Поэтому целесообразно заменить тангенсы через синусы и косинусы соответствующих аргументов.

13.5. Если записать ¹/_{tg x} вместо ctg x, то после простых преобразований (следите за их равносильностью) придем к распадающемуся уравнению.

13.6. Прибавить к левой и правой частям уравнения tg 3x. Тогда слева можно вынести за скобки число 3, а справа tg 3x.

13.7. Нетрудно заметить, что множитель sin (x + ^π/₄) можно вынести в левой части уравнения за скобки, так как он получается при преобразовании суммы sin x + cos x в произведение.

13.8. Перенести tg 2x в правую часть и привести обе части уравнения к виду, удобному для логарифмирования.

13.9. Избавиться от иррациональностей с помощью перехода под радикалами к функциям половинного аргумента. Использовать условие, что 0 < x < 2π, и постараться раскрыть знаки абсолютной величины.

13.10. Перенести sin α в левую часть и привести полученную сумму к виду, удобному для логарифмирования. Стоящий в правой части sin x выразить через функции половинного аргумента.

13.11. Рассмотреть случаи, позволяющие раскрыть знаки абсолютной величины; задача сведется к решению двух уравнений и к выбору тех значений x, которые попадают в указанный интервал.

13.12. Вначале следует посмотреть, не стоит ли под радикалом полный квадрат какого-то выражения. Число 16 нам, скорее всего, не помешает, а вот число 17 менее удобно для последующих преобразований. Чтобы освободиться от его присутствия, удобно вынести под радикалом sec² x за скобки, а оставшееся в скобках выражение записать через sin x.

13.13. Перенести все члены уравнения в левую часть и разложить на множители с тем, чтобы появилась возможность избавиться от большинства радикалов.

13.14. Выразить sin 4x через tg 2x. Это тождество условное, поэтому нужно убедиться в равносильности полученного уравнения данному.

13.15. Перейти к функциям sin x и cos x.

13.16. Правую часть уравнения можно сократить на cos 2x, добавив условие cos 2x ≠ 0.

13.17. С помощью универсальной подстановки (через тангенс половинного угла) это уравнение может быть сведено к кубичному уравнению относительно у = tg ^x/₂. Равносильное ли получится уравнение?

13.18. Понизить степень.

13.19. Левую и правую части можно привести к виду, удобному для логарифмирования.

13.20. Уравнение упростится, если преобразовать произведения, стоящие в левой его части, в разность косинусов. Оно станет квадратным относительно у = cos x. (!)

13.21. Выразить sin 4x через sin x и cos x и вынести sin x за скобки после переноса в левую часть.

13.22. Раскрыть скобки и каждое из ста произведений преобразовать в сумму. (!)

13.23. Каждое произведение преобразовать в разность косинусов. (!)

13.24. Выразить cos 4x + 1 через cos 2x.

13.25. Произведение косинусов может равняться единице, если либо оба косинуса равны единице, либо оба равны минус единице.

13.26. Представить единицу в виде sin² x + cos² x.

13.27. Уравнение таково, что не остается надежд на упрощения в результате тригонометрических преобразований. Поэтому следует попытаться воспользоваться оценками. Во-первых, выражение, стоящее в левой части, всегда неотрицательно, кроме того, cos⁴ x ≥ 0; следовательно, и cos 3x ≥ 0. Во-вторых, слева стоит сумма квадратов, которую разумно дополнить до полного квадрата.

13.28. Обратить внимание на то обстоятельство, что левая часть уравнения не может стать меньше единицы, а правая не может превзойти единицу.

13.29. Второе уравнение легко свести к виду sin (2x − у) = 0, откуда у = 2x − πk. При подстановке в первое уравнение получим

4 tg 3x = 3 tg 4x.

Это уравнение удобнее преобразовать к виду

4(tg 4x − tg 3x) = tg 4x,

чем к виду

3(tg 4x − tg 3x) = tg 3x,

так как множитель 4 удобнее при тригонометрических преобразованиях.

13.30. Второе уравнение легко решается преобразованием его левой части в разность косинусов; в результате получится соотношение 2у = ^π/₂ − x + kπ. Прежде чем им воспользоваться, следует первое уравнение привести к виду, удобному для логарифмирования.

13.31. Левые части первого и второго уравнений нетрудно выразить через u = sin x и v = sin у.

13.32. Второе уравнение существенно упростится, если его левую часть преобразовать в сумму.

13.33. Из системы можно исключить x, если воспользоваться основным тригонометрическим тождеством

sin² φ + cos² φ = 1.

13.34. Нужно вначале решить первое уравнение, решение которого находится обычным путем. Найденное значение подставить во второе уравнение.

13.35. Разделив второе уравнение на первое, получим tg у = 2 tg x.

13.36. Удобно перейти к уравнениям относительно одной тригонометрической функции. При этом нужно следить за равносильностью.

13.37. Если возвести каждое уравнение в квадрат и полученные уравнения сложить, то мы исключим α. Однако для нас важнее исключить либо x, либо у. Как это сделать?

13.38. Левую часть первого уравнения можно преобразовать в разность sin (x − у) − cos (x + у). Из второго уравнения определяется cos (x + у).

13.39. Правая часть уравнения не может стать больше четырех. Если ввести обозначения tg² x = u, tg² у = v, то нетрудно заметить, что левая его часть не может стать меньше четырех.

13.40. Способ 1. Умножить sin² x на тригонометрическую единицу sin² 3x + cos² 3x и сгруппировать члены, содержащие sin² 3x.

Способ 2. Перенести все члены в левую часть и выделить полный квадрат разности 2 sin x − sin² 3x. Оставшиеся члены образуют неотрицательное выражение.

13.41. Способ 1. Преобразовать сумму тригонометрических функций cos x + cos у в произведение, а cos (x + у) выразить через косинус половинного аргумента.

Способ 2. Раскрыть cos (x + у) по формуле косинуса суммы.

13.42. Вопрос задачи естественно поставить следующим образом: при каких а и b равенство

tg x + tg (а − x) + tg x tg (а − x) = b

является тождеством (неабсолютным)?

13.43. Вначале следует попытаться оценить снизу левую часть уравнения, так как верхняя оценка правой части очевидна:

12 + ½ sin у ≤ 12,5.

13.44. Перенести sin Зx в левую часть уравнения и преобразовать sin x − sin Зx к виду, удобному для логарифмирования.

13.45. После раскрытия скобок произвести упрощения.

13.46. Условие записано таким образом, что введение нового неизвестного

является очевидным шагом к решению уравнения. Мы придем к квадратному уравнению относительно у.

13.47. В задаче требуется решить систему двух уравнений с одним неизвестным и выбрать решения, удовлетворяющие ограничению |x| < 5. Было бы заблуждением пытаться свести эти два уравнения в одно с помощью подстановки или какого-либо другого преобразования. Можно решить каждое в отдельности и отыскать общие корни. Однако попытайтесь использовать особенности данной системы.

13.48. Так как выражений, схожих с cos ^6x/₅ , в условии больше нет, то, скорее всего, cos ^6x/₅ преобразовывать не следует. В числителе левой части tg x естественно вынести за скобки. Выражение 3 − tg²x, оставшееся в скобках, удобнее преобразовать, заменив tg² x на

13.49. Воспользуйтесь тем, что

и cos Зx + cos x = 2 cos 2x cos x.

13.50. Разбить 4 ctg 2x на слагаемые и в левой части образовать выражения 2(tg x + ctg 2x), tg ^x/₂ + ctg 2x, ctg 2x − ctg Зх. Преобразовать каждое из этих выражений и затем преобразовать все уравнения к равной нулю дроби, у которой числитель и знаменатель — произведения тригонометрических функций.

13.51. Сделайте преобразование, имея в виду, что sin t ≠ 0, cos t ≠ 0, и воспользуйтесь соотношениями:

K главе 14

14.1. Если обе части неравенства возвести в квадрат, то получим равносильное неравенство. (!)

14.2. Использовать тот же прием, что и при решении уравнения cos x − sin x = −1, т. е. ввести вспомогательный угол. (!)

14.3. Способ 1. Можно перейти к неравенству относительно tg x. При этом придется рассмотреть различные случаи, в зависимости от знака cos x. (!)

Способ 2. Если синус и косинус выразить через tg ^x/₂, то получим квадратное неравенство. Равносильно ли оно данному? (!)

14.4. Если cos 2x и sin 2x выразить через tg x и обозначить tg x = y, то получится простое алгебраическое неравенство. Равносильно ли оно данному?

14.5. Способ 1. Можно перейти к совокупности двух систем: cos x и tg 2x должны быть нестрого (т. е. включая нуль) разных знаков.

Способ 2. Воспользоваться формулой тангенса двойного угла. Равносильное ли получится неравенство?

14.6. Неравенство можно привести к алгебраическому, если выразить все тригонометрические функции через cos x. (!)

14.7. Если записать sin 2x = 2 sin x cos x и перенести все члены неравенства в одну часть, то получим однородное выражение относительно sin x и cos x. Разделив на cos² x, получим алгебраическое неравенство относительно y = tg x. Равносильно ли оно данному? (!)

14.8. Вычислить дискриминант и выяснить, когда он положителен.

14.9. Неравенство может выполняться только при sin x ≥ 0 и cos x ≥ 0. Приняв во внимание эти ограничения, его можно возвести в квадрат. (!)

14.10. Записать решение неравенства в предположении, что

— новое неизвестное.

14.11. Привести к неравенству относительно одной тригонометрической функции.

14.12. Перенести −1 в левую часть, записать тангенсы через синусы и косинусы и выполнить сложение.

14.13. Это — иррациональное неравенство относительно у = cos x. Не следует забывать, что |у| ≤ 1. Благодаря этому решение можно упростить.

14.14. Если выразить sin x и cos x через tg ^x/₂ , то получим алгебраическое неравенство, которое решается методом интервалов. (!)

14.15. Выразить все тригонометрические функции через sin α.

14.16. Так как sin² x ≥ 0, то, заметив, что x = πk — решения неравенства, можно изолировать параметр а², разделив обе части неравенства на sin² x.

14.17. Если обозначить cos t = z, то данное выражение запишется в виде квадратного трехчлена относительно z, который должен быть положительным при всех −1 ≤ z ≤ 1. Найдите абсциссу вершины соответствующей ему параболы.

K главе 15

15.1. В правой части можно произвести логарифмирование, не нарушая равносильности.

15.2. Рассмотреть случаи 0 < tg x < 1 и tg x > 1. Удобно выразить sin² x через tg² x. (!)

15.3. Нетрудно заметить, что на самом деле интервал можно сузить: 0 < x < ^π/₂ , так как при ^π/₂ < x < π функции, стоящие под знаком логарифма, отрицательны.

15.4. Вначале нужно привести все логарифмы к общему основанию с помощью формулы log_a^k N = ¹/_k log_a N.

15.5. Неравенство эквивалентно условию, что основание логарифмов лежит между 0 и 1.

15.6. Начать следует с приведения левой части к виду, удобному для логарифмирования. Это позволит перейти к неравенствам, где уже не будут участвовать тригонометрические функции.

15.7. Использовать тот факт, что arccos у ≥ 0. Чему равносильно данное в условии неравенство?

15.8. Область значений левой части неравенства — интервал от 0 до ^π/₂ , а область значений правой части — интервал от 0 до π. Так как левая часть должна быть больше правой, то аргумент арккосинуса не может стать отрицательным.

15.9. Второй сомножитель неотрицателен при всех x, следовательно, неравенство может удовлетворяться лишь при положительных значениях первого сомножителя. Если произведение двух положительных чисел не меньше единицы, то хотя бы одно из них не меньше единицы.

15.10. Обозначим первый сомножитель через А, а второй через В. Так как А ≥ 0, то неравенство равносильно совокупности двух систем:

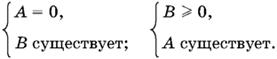
K главе 16

16.1. Правая часть уравнения не может стать меньше двух. Сравнить с оценкой левой части. (!)

16.2. Это уравнение легко привести к квадратному относительно 2^tg²x. (!)

16.3. Перейти к общему основанию. Не нарушится ли при этом равносильность?

16.4. Поскольку в левой части уравнения стоит произведение синуса и косинуса от одного аргумента, удобно воспользоваться формулой синуса двойного угла. Записать, чему равен аргумент.

16.5. Перейти к уравнению без логарифмов, позаботившись о сохранении ограничений.

16.6. Ввести вспомогательное неизвестное и преобразовать данное уравнение в квадратное. (!)

16.7. От этого уравнения легко перейти к тригонометрическому. При этом нужно учесть все ограничения, которыми логарифм связывает число и основание.

16.8. Уравнение равносильно уравнению

при условии, что cos² x ≠ ¹/₈.

16.9. Перейти к уравнению 5π(½)^x = ^π/₄ + πk и найти все k, при которых это равенство возможно.

16.10. Вначале решить квадратное уравнение относительно lg cos x. Затем найти cos x и на этом шаге провести исследование.

16.11. Решить квадратное уравнение и учесть все ограничения на параметр а в связи с появлением радикала и синуса.

16.12. Данную систему нужно заменить системой без логарифмов. Однако при этом следует помнить обо всех ограничениях, которые накладываются на число, стоящее под знаком логарифма, и на основание логарифма.

16.13. Уравнение составлено таким образом, что решить его с помощью элементарных преобразований нельзя. Остаются два пути: либо графическое решение, либо оценка правой и левой частей уравнения. Второй путь предпочтительнее, так как левая часть легко оценивается, если положить 4^{cos² − πx} = u.

16.14. Трехчлен x² − x + 0,5 всегда больше 0,25.

K главе 17

17.1. Данную систему решить относительно f(2x + 1) и g(x − 1).

17.2. f(x) = x(x² − 6x + 9) = x(x − 3)²,

f(f(x)) = f(x) (f(x) − 3)² = x(x − 3)²(x³ − 6x² + 9x − 3)².

17.3. Из второго уравнения найти 2 и подставить в первое. Воспользоваться условием, что x и у — целые числа.

17.4. Неравенство |x + 2| ≤ x + 2 удовлетворяется при всех x ≥ −2.

Уравнение следует преобразовать с помощью подстановки

2^{x − 1} = у, sin ^πx/₂ = 2.

17.5. Найти первообразную F(x) и воспользоваться условием касания графиков функций f(x) и F(x) в некоторой точке F₀(x₀; у₀).

17.6. Данное неравенство равносильно такому:

Рассмотрите случаи: а) 0 < x − у < 1 и б) x − у > 1.

17.7. Изобразите на графике часть плоскости, координаты точек которой удовлетворяют первому неравенству, для каждого квадранта отдельно. Для первого квадранта это будут все его точки.

17.8. Начать нужно с определения координат точки E. Для этого придется записать уравнение прямой, проходящей через две точки (x₁, у₁) и (x₂, у₂):

сначала для точек В и D, затем для точек А и C. Решение системы этих двух уравнений даст нам координаты точки E.

17.9. Оба неравенства зависят от x + у и от у − x. Это подсказка побуждает ввести новые переменные u = x + у и v = у − x.

17.10. Если x₁ и x₂ — целые, то и а — целое. (Докажите.)

17.11. Это биквадратное уравнение, и оно сводится к квадратному подстановкой x² = у. Знак дискриминанта квадратного уравнения не позволяет ответить на вопрос о числе корней исходного уравнения. Нужно позаботиться, чтобы у ≥ 0.

17.12. Поскольку cos 8x = 1 − 2 sin² 4x, исходное уравнение преобразуется в квадратное относительно у = sin 4x, где |у| ≤ 1.

17.13. Подставив любые значения x и а в данное уравнение, получим соответствующее единственное значение у. Таким образом, при любом фиксированном а любая прямая, параллельная оси у, пересечет кривую семейства, соответствующую этому а, в единственной точке. Это не означает, что через каждую точку плоскости (x, у) проходит кривая семейства. Не при любом у мы найдем точки плоскости (x, у), соответствующие данному семейству.

K главе 18

18.1. Если ввести в качестве неизвестных производительности труб, то получим три уравнения с четырьмя неизвестными (объем бассейна следует принять за единицу).

18.2. Если плечи весов равны l₁ и l₂, то можно вычислить массу P товара, отпущенного покупателю.

18.3. Эта задача менее всего похожа на «алгебраическую». Скорее, она напоминает рассуждения человека, пытающегося обнаружить факт на основе отрывочных сведений. Вначале следует обратить внимание на то обстоятельство, что листов в альбоме — число целое. После этого нужно использовать условие задачи с тем, чтобы ограничить рассмотрением возможные значения этой переменной.

18.4. Путь буксира изображен на рис. 1.18.4, где x — часть пути, которую прошел самостоятельно (т. е. без буксировки) первый понтон, а y — часть пути, которую прошел без буксировки второй понтон.

18.5. Так как некто родился в девятнадцатом веке, то неизвестны две последние цифры его года рождения. Если мы обозначим их через x и y, то сможем записать условия задачи в виде уравнений.

18.6. Если одна часть имеет массу x карат, то ее цена lx², где l — коэффициент пропорциональности.

18.7. Основная трудность в выборе неизвестных, которые позволили бы связать данные в условии величины. Здесь эту роль могут выполнить нормы расхода горючего при работе двигателя с фиксированной собственной скоростью. K чему удобнее отнести эти нормы: к часу работы двигателя или к километру пути в стоячей воде?

18.8. Выбор неизвестных подсказан условием задачи: x, y, z, s и t — число десятков порций соответствующих сортов мороженого. Выбрав в качестве неизвестных число десятков порций, а не число самих порций, и заметив, что неизвестные — натуральные числа, мы тем самым использовали условие, в силу которого у продавца есть по нескольку десятков порций мороженого. Последнее условие задачи запишется в виде неравенства y > s. Это ограничение позволит нам восполнить отсутствие пятого уравнения в системе с пятью неизвестными.

18.9. Пусть С — устье реки. Время, за которое плоты прошли весь путь от А до В, известно, а время, за которое прошли путь СB, обозначим через x. Если ввести в рассмотрение расстояние AC, то скорость течения реки можно выразить из остальных условий задачи.

18.10. Условия задачи отражены на схеме (рис. 1.18.10). С помощью схемы можно составить четыре уравнения: встреча в точке С дает два уравнения и две оставшиеся встречи — по одному.

18.11. Вначале нужно проследить весь процесс за один цикл в предположении, что объем сосуда принят за единицу, а часть его объема, занимаемая раствором, обозначена через x.

18.12. В качестве неизвестных удобно выбрать: x — скорость автомобиля, y — скорость мотоцикла и z — расстояние между пунктами А и В. Первая встреча произошла через ^z/_{x + у} ч после начала движения на расстоянии ^zy/_{x + у} км от пункта В.

Теперь нетрудно подсчитать расстояние между пунктами первой и второй встречи.

18.13. В качестве неизвестных удобно выбрать расстояние (x), которое пассажир проехал на такси и (y) на автобусе, скорость поезда (u) и время, на которое пассажир опоздал на поезд (t).

18.14. Скорости поездов связаны со всеми величинами, участвующими в задаче. Поэтому естественно ввести в качестве неизвестного x скорость товарного поезда до остановки. Тогда mx — скорость пассажирского поезда до остановки.

Однако одного неизвестного здесь мало, так как поезда выходили из своих пунктов в разное время. Чтобы связать скорости и времена, нам нужно ввести в рассмотрение расстояния. Пусть расстояние между А и В равно y, а расстояние между А и С равно z.

18.15. Вопрос задачи не имеет прямого отношения к ее решению. Поэтому величину, о которой спрашивается в задаче, не следует выбирать в качестве неизвестного, так как она сложно связана с остальными компонентами. Наиболее удачно связать участвующие в задаче величины — расстояния и промежутки времени — можно с помощью скоростей самолета и вертолета.

18.16. Если обозначить устье реки, на которой стоит порт M, буквой А, а устье второй реки буквой В, то для решения задачи удобно ввести два неизвестных расстояния. Сразу же появляется желание обозначить расстояние AB, которое требуется определить, буквой x, один из оставшихся отрезков, МА или NA, — буквой у, а последний отрезок записать как s − (x + у). Однако более естественно не нарушать симметрию и обозначить буквами x и у отрезки МА и BN соответственно. Тогда отрезок AB будет равен s − (x + у). Поскольку нас интересует только отрезок AB, то нужно определить x + у.

18.17. Поскольку линейные единицы измерения в условие не входят, целесообразно принять расстояние между А и В за единицу. Если ввести скорости поездов: u — скорого, v — пассажирского, 2v — курьерского, то легко определить u в долях AB в час.

18.18. Первый вопрос, который должен возникнуть у хозяйственника, решающего подобную задачу, какой из комплектов выгоднее заказать, т. е. для какого из них средние расходы на пересылку одной детали будут наименьшими.

K главе 19

19.1. Записать выражения для и_n и и_{n + 1} и сравнить.

19.2. Поскольку первый член арифметической прогрессии входит в качестве слагаемого в выражения для любого ее члена, удобнее сразу записать a_q − а_р, a_r − a_q, a_s − а_z. Это тем более удобно, что нас интересуют разности p − q, q − r, r − s.

19.3. Если ввести а₁ и u₁ — соответственно первые члены арифметической прогрессии с разностью d и геометрической прогрессии со знаменателем q, то а, b и с придется выразить через а₁, u₁, d и q.

19.4. В левой части удобно перейти к общему основанию x.

19.5. Если бы сумма состояла из одних девяток, то каждый член можно было бы представить в виде 10^k − 1.

19.6. Выражение, стоящее под знаком квадратного корня, умножить и разделить на 9. Число, состоящее из k девяток, равно 10^k − 1.

19.7. Условия задачи можно записать в виде а₁ + а₃ = 2а₂, а₁а₃ = а₂² . Из этой системы нетрудно исключить а₂.

19.8. Удобно ввести знаменатель прогрессии q и с его помощью записать теорему Виета для обоих уравнений. Это позволит определить q и x₁. (!)

19.9. Так как корни уравнения образуют геометрическую прогрессию, то x₂ = x₁q, x₃ = x₁q². Воспользуйтесь теоремой Виета для уравнения третьей степени.

19.10. Если приравнять выражения для удвоенной суммы n членов прогрессии и суммы всех ее членов, то получим уравнение относительно qⁿ.

19.11. Так как число делится на 45, то оно может оканчиваться либо нулем, либо пятью. Рассмотреть эти два случая.

19.12. Если обозначить через x цифру единиц, а через q — знаменатель прогрессии, то легко составить два уравнения, отражающих условия задачи. Однако можно пойти по другому пути: поскольку цифры числа образуют геометрическую прогрессию и само число больше 594, то в нашем распоряжении только три возможности: 931, 842 и 964. (!)

19.13. Всю работу следует принять за единицу. Чтобы использовать условия задачи, нужно знать производительность одного комбайна. Однако нам неизвестно, сколько часов перед завершением работы по плану все комбайны работали вместе. Поскольку удобнее вводить одноименные неизвестные, то эту величину обозначим через y, а через x обозначим количество часов, необходимых одному комбайну, чтобы убрать весь урожай. Тогда производительность комбайна будет равна ¹/_x.

19.14. Пусть братьям а, аq и аq² лет. Если младший получит x рублей, то остальные два получат xq и xq² рублей. Условия задачи позволяют составить три уравнения.

19.15. После того как числа, о которых говорится в задаче, будут обозначены буквами а, b и с и условия задачи будут переведены на математический язык, мы получим два уравнения с тремя неизвестными. Достаточно ли этого, чтобы решить задачу?

19.16. Воспользоваться методом математической индукции, что позволит доказать формулы для а_n и b_n.

19.17. Решив данное тригонометрическое уравнение, получим две серии углов, каждая из которых является арифметической прогрессией с известной разностью и первым членом, равным нулю. В каком случае две арифметические прогрессии могут быть объединены в одну?

K главе 20

20.1. Данное неравенство эквивалентно такому:

¹/_2² + ... + ¹/_n² < 1.

Оценить каждое слагаемое так, чтобы легко было оценить всю сумму, стоящую слева.

20.2. Домножить все члены на d.

20.3. Чтобы разложить дробь

на простейшие, можно начать с разложения дроби

, а результат умножить на

.

20.4. Слева стоит сумма членов геометрической прогрессии.

20.5. Выписать все коэффициенты многочлена 1 + x + 2x² + ... + nxⁿ и под ними написать коэффициенты того же многочлена, записанные в обратном порядке. Рассмотреть сумму произведений стоящих друг под другом чисел.

20.6. В левой части неравенства стоит абсолютная величина суммы членов бесконечной геометрической прогрессии со знаменателем −2x.

20.7. Каждое слагаемое k · k! можно представить в виде (k + 1)k! − k(k − 1)!. При этом следует иметь в виду, что 0! = 1. (!)

20.8. Коэффициенты в правой части образуют арифметическую прогрессию с разностью 3. Если домножить S_n на x², то справа получим сумму, все члены которой, кроме крайних, имеют коэффициент, отличающийся от подобного коэффициента S_n на 3.

20.9. Рассмотреть тождество

(x + 1)⁵ = x⁵ + 5x⁴ + 10x³ + 10x² + 5x + 1

и положить в нем последовательно x = 1, 2, ..., n.

20.10. В n-й группе n членов. Рассмотрите отдельно случаи, когда n четное и n нечетное.

20.11. Удобнее найти 2S_n sin ^π/_2n.

20.12. Можно разбить эту сумму на 1 00 сумм:

каждая из которых является суммой членов геометрической прогрессии. Однако попытайтесь решить эту задачу проще, обозначив искомую сумму через в и осуществив над ней некоторое несложное преобразование.

20.13. Общий член ряда имеет вид

Чтобы воспользоваться формулой геометрической прогрессии, нужно избавиться от 2 n в числителе. Чтобы понять, как это лучше сделать, запишите рядом два соседних члена ряда.

K главе 21

21.1. Если все, сидящие за круглым столом, одновременно сдвинуться на один стул в одном направлении, то у каждого останутся те же самые соседи.

21.2. Представить искомое число в виде разности числа всех перестановок из пяти элементов и перестановок, не удовлетворяющих условиям задачи.

21.3. Три разряда каждого числа должны быть заняты двойками. В оставшиеся четыре разряда можно поместить любые из восьми цифр, что даст 8⁴ вариантов.

21.4. Задачу следует начать решать в предположении, что есть разные цифры l₁, l₂ и l₃, которые входят в каждое число, а остальные пять цифр равноправны.

21.5. Легче найти число всевозможных размещений экскурсантов по каютам в предположении, что каюты неравноценны. Пусть таких размещений будет N, а размещений, о которых идет речь в задаче, K. Поскольку из каждого размещения экскурсантов по равноценным каютам можно получить 8! размещений по неравноценным каютам, то K · 8! = N.

21.6. В записи k-го члена суммы произвести сокращение на k.

21.7. Нужно найти такие n, для которых равенство

выполняется при некотором k.

21.8. Представить а + b + с + d в виде (а + b) + (с + d) и осуществить возведение в n-ю степень по правилам возведения в степень двучлена.

21.9. Коэффициент при x^k будет равен числу членов, содержащих x^k при почленном перемножении двух одинаковых многочленов. Придется различать случай, когда члены, содержащие x^k, могут быть получены в результате умножения друг на друга членов суммы 1 + x + x² + ... + x^{k − 1} + x^k (0 ≤ k ≤ n − 1), от случая, когда n − 1 < k ≤ 2(n −1).

21.10. Записать выражение для общего члена разложения и сравнить с выражением для десятого члена разложения.

21.11. Сгруппировать члены внутри скобки и последовательно дважды применить формулу бинома.

21.12. Если обозначить через Р_n число способов, которыми можно разбить на группы последовательность из n элементов, то можно получить рекуррентную формулу для Р_n.

21.13. Если на плоскости проведены m параллельных прямых, то они разбивают плоскость на m + 1 частей. Когда мы пересечем их некоторой прямой, то каждая часть разобьется на две. Что произойдет, если к уже проведенным k непараллельным прямым добавить еще одну?

K главе 22

22.1. Перенести acrtg ⁷/₂₃ в правую часть, после чего оценить значения обеих частей с тем, чтобы они попали в интервал (0, ^π/₂). (!)

22.2. Каждое из двух первых слагаемых лежит в интервале (0, ^π/₄). Это позволяет воспользоваться формулой тангенса суммы и заменить два первых слагаемых одним.

22.3. Начать нужно с представления в виде значения одной тригонометрической функции первого и третьего слагаемых. Чтобы их сумма попала в область главных значений арккотангенса, придется прибавить к ней π. (!)

22.4. Если 0 ≤ x ≤ 1, то сумма существует и лежит в интервале [0, π], т. е. в интервале монотонности косинуса.

22.5. Начать нужно с выяснения, в каком интервале лежит π(x² + x − 3), если 0 ≤ x ≤ ^{√3 − 1}/₂.

22.6. Убедившись в существовании арксинусов при 0 ≤ x ≤ 1, перенести ^π/₄ в левую часть, а вычитаемое — в правую, затем доказать, что левая часть равенства будет лежать в интервале монотонности синуса. (!)

22.7. Так как x < −1, то значение каждой функции, входящей в правую часть, можно уточнить с тем, чтобы сумма попала в интервал монотонности синуса и тангенса. (!)

22.8. Из данного уравнения можно найти значения arcsin x. Из этих значений остается выбрать те, которые лежат в области значений арксинуса. (!)

22.9. Поскольку arcsin x — нечетная функция, то одновременно с корнем x уравнение имеет корень −x. Это позволяет искать лишь неотрицательные корни.

22.10. Из условия следует, что x > 0. Левая часть заключена в интервале [0, π], который является интервалом монотонности косинуса.

22.11. Воспользовавшись тем, что 2 + cos x > 0 и 2 cos² x/₂ ≥ 0, можно уточнить интервал значений левой части уравнения.

22.12. Левая и правая части лежат в интервале монотонности синуса. (!)

22.13. Уточнение интервалов с тем, чтобы получить равносильное уравнение, приведет к нерациональному способу решения. Проще перенести, например, arctg (x + 1) в правую часть и взять котангенсы от обеих частей. Каким образом может быть нарушена равносильность?

K главе 23

23.1. Поскольку sin x ≤ 1, то log₃ sin x ≤ 0. (!)

23.2. В указанной последовательности действий первое ограничение накладывается на трехчлен x² − x − 1, он должен быть положительным. Следующее ограничение накладывается уже на log_½ (x² − x − 1). (!)

23.3. Нужно пройти всю последовательность действий, начиная с самого внутреннего, и записать все встречающиеся при этом ограничения. (!)

23.4. Найдя область определения функции arccos (x² − 3x + 1), исключить точки, в которых не существует tg 2x. (!)

23.5. Решить графически систему неравенств, обеспечивающих существование данного выражения. (!)

23.6. Способ 1. Доказательство можно вести от противного, предположив, что функция имеет период T.

Способ 2. Найти корни функции и исследовать их в предположении, что у функции имеется период.

23.7. Записать тождество, равносильное условию, что f(x) имеет своим периодом число T. Рассмотреть это тождество при x = 0 и x = ±T. (!)

23.8. Ясно, что любое общее кратное периодов cos ^3x/₂ и sin ^x/₃ будет периодом данной функции. Доказать, что наименьшее общее кратное будет основным периодом.

K главе 24

24.1. Заменить cos² x на 1 − sin² x. В результате получится квадратный трехчлен относительно sin x.

24.2. Записать у как одну функцию другого аргумента.

24.3. Привести к одной тригонометрической функции другого аргумента.

24.4. Выражение можно представить в виде А² + В² + С, где С — константа.

24.5. Чтобы раскрыть знаки абсолютных величин, нужно нанести на числовую ось точки ±1 и ±2, которые разобьют ее на пять интервалов.

24.6. Воспользоваться неравенством между средним арифметическим и средним геометрическим нескольких чисел.

24.7. Чтобы найти максимум AB + BC, удобно ввести углы x и у (рис. 1.24.7), имея в виду, что x + у = π − α, и перейти с помощью теоремы синусов к тригонометрическим соотношениям. (!)

24.8. Если обозначить катеты основания через а и b, то боковая поверхность призмы равна

причем ab = 4.

24.9. Квадрат должен быть вписан в шестиугольник так, чтобы не нарушалась симметрия, т. е. центр квадрата должен совпадать с центром шестиугольника.

24.10. Прежде всего необходимо обратить внимание на свойства квадратного трехчлена, стоящего в знаменателе. Его дискриминант отрицателен и, следовательно, трехчлен не может быть равен нулю при действительных x.

Если обозначить теперь данную дробь через у, то можно получить квадратное уравнение относительно x, в котором у играет роль параметра.

24.11. Если ребра параллелепипеда обозначить через а, b и с, то условие задачи можно записать в виде системы

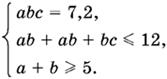
Из второго и третьего неравенств следует, что

ab + с(а + b) ≥ ab + 5с.

24.12. Чтобы найти наименьшее значение этой функции, естественно выделить полный квадрат. Однако удобнее вначале перейти от котангенсов к косекансам, что позволяет выразить функцию только через синусы:

Теперь в числителе следует выделить полный квадрат разности. При этом могут представиться два случая, в зависимости от знака произведения sin (α + x) sin (α − x). Чтобы не рассматривать их отдельно, можно необходимые преобразования записать так:

sin² (α + x) + sin² (α − x) = [|sin (α + x)| − |sin (α − x)|]² + 2 |sin (α + x) sin (α − x)|.

24.13. Известно, что arcsin x + arccos x = ^π/₂ . Поэтому данную функцию удобно преобразовать так, чтобы воспользоваться этим соотношением.

24.14. Воспользоваться преобразованием нормирования:

после чего коэффициенты при sin α и cos α можно объявить косинусом и синусом общего аргумента φ, т. е.

Функция у достигает своего наименьшего значения

когда sin (α + φ) = −1, и наибольшего значения

при sin (α + φ) = 1. (!)

24.15. Систему естественно привести к виду

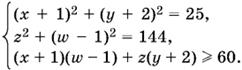
Свободные члены равны, соответственно, 5², 12² и 5 · 12. Удобно каждое из соотношений разделить на его свободный член.