Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003

Решения
Геометрические задачи на плоскости

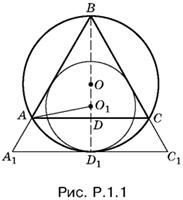
1.1. Треугольник А₁BC₁ (рис. P.1.1) правильный, так как он подобен данному треугольнику ABC. Точки B, О, О₁ и D лежат на одной прямой. Чтобы найти АО₁, нужно вычислить O₁D. Но O₁D = O₁D₁ − DD₁. Отрезок O₁D₁ равен трети отрезка ВD₁, как радиус окружности, вписанной в правильный треугольник А₁BC₁. Таким образом, O₁D₁ = ^2R/₃ . Отрезок DD₁ мы найдем, если рассмотрим треугольник ABC, как вписанный в окружность с центром О:

DD₁ = ^R/₂.

Отсюда O₁D = ^2R/₃ − ^R/₂ = ^R/₆ . Так как АD = ½ AC = ^{R √3}/₂, то

Ответ. R ^√7/₃

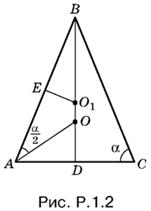
1.2. B треугольнике AOB (рис. P.1.2) известны: ∠ BAO = ^α/₂ , ∠ AOB = ^α/₂ + ^π/₂, BO = m· По теореме синусов находим AB = m ctg ^α/₂· Теперь можно найти AC и R = ВО₁:

AC = 2AD = 2АВ sin (^π/₂ − α) = 2АВ cos α = 2m ctg ^α/₂ cos α,

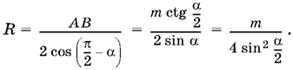
Ответ.

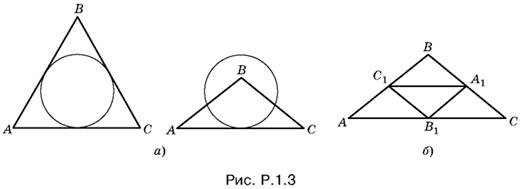
1.3. Условие задачи может быть геометрически осуществлено в двух случаях (рис. Р.1.3, а), т. е. когда треугольник либо правильный, либо равнобедренный тупоугольный (докажите). Решить эту задачу можно сразу для обоих случаев. На рис. Р.1.3, б изображены треугольник ABC и треугольник А₁В₁С₁, составленные из средних линий первого треугольника. Треугольник А₁В₁С₁ подобен треугольнику ABC с коэффициентом подобия половина. Следовательно, радиусы окружностей, описанных около этих треугольников, относятся как один к двум.

1.4. Если сторона а треугольника ABC биссектрисой АА₁ разделена на отрезки а₁ и а₂, то можно записать следующие соотношения (рис Р. 1.4.):

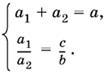
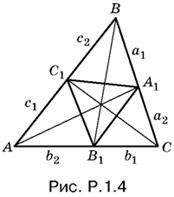
Решая эту систему уравнений относительно a₁ и а₂, получим

Вычислим аналогично отрезки, на которые разделены стороны b и с треугольника ABC:

Так как отношение площадей треугольников, имеющих общий угол, равно отношению произведений сторон, между которыми лежит этот общий угол, то

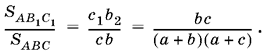
Аналогично находим

Теперь найдем отношение

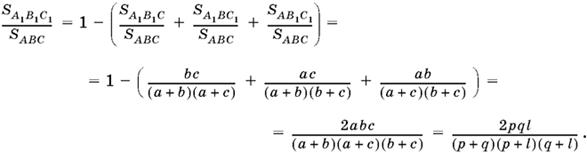
Ответ.

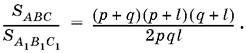
1.5. Выразим площадь треугольника ABC через радиус r вписанной окружности и углы А, B и С треугольника. Вначале запишем

S_ABC = S_AOB + S_BOC + S_COA

(рис. P.1.5).

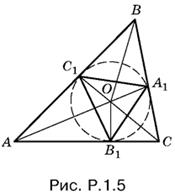
Так как

S_AOB = ½АО · ВО sin OB,

где

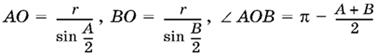
и, следовательно, sin ∠AOB = sin ^{A + B}/₂ = cos ^C/₂ , то

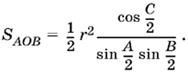
Аналогично находим S_BOC и S_COA и вычисляем искомую площадь:

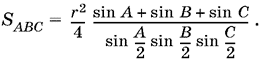
Выразим теперь через r, А, B и С площадь треугольника А₁В₁С₁. Разобьем и его на три треугольника:

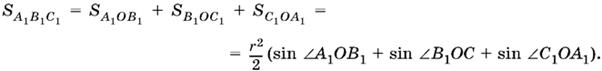
Чтобы найти угол А₁ОВ₁, рассмотрим четырехугольник А₁ОВ₁С. B этом четырехугольнике два угла прямых, а потому два других — угол А₁ОВ₁ и угол С — образуют в сумме развернутый угол, т. е. угол А₁ОВ₁ равен π − С. Аналогично находим углы В₁ОС₁ и С₁ОА₁.

Итак,

Остается найти отношение

Ответ. 2 sin ^A/₂ sin ^B/₂ sin ^C/₂ .

1.6. Так как B = 3С, то из соотношения между площадями мы получим

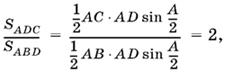
т. е. ^АС/_AB = 2, откуда, в силу теоремы синусов, ^{sin B}/_{sin C} = 2. Вспоминая, что по условию B = 3С, придем к тригонометрическому уравнению sin 3С = 2 sin С. Домножим обе части уравнения на cos С, получим sin 3С cos 3С = sin 2С. Преобразовав левую часть в сумму синусов, придем к уравнению

sin 4С + sin 2С = 2 sin 2С, или sin 4С = sin 2С.

Так как C — угол треугольника, меньший 1 (ведь 3C и C — углы одного треугольника), то последнее уравнение может выполняться только в том случае, если

4C = π − 2C, т. е. C = ^π/₆ .

Находим остальные углы:

B = 3С = ^π/₂, A = ^π/₃.

Ответ. ^π/₃, ^π/₆, ^π/₂.

1.7. С одной стороны, площадь треугольника CAD (рис. Р.1.7) можно выразить через стороны b, l и угол между ними, а с другой стороны, — как сумму площадей треугольников АВС и ABD:

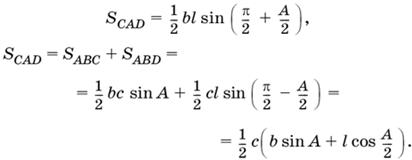
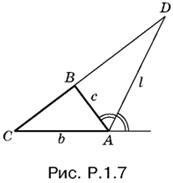
Приравнивая эти два выражения, найдем l(b − c) cos ^A/₂ = bc sin A,

или

l(b − c) cos ^A/₂ = 2bc sin ^A/₂ cos ^A/₂.

Так как cos ^A/₂ в треугольнике не может быть равен нулю, то на него можно сократить. Теперь найдем l.

Ответ.

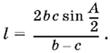
1.8. Воспользуемся сравнением площадей. С одной стороны, S = pr = ^{a + b + c}/₂r, где через а обозначена искомая сторона. Находим отсюда, что 2S = ar + (b + c)r. С другой стороны, если биссектрису угла А обозначить через l_a, то

S = ½ l_ab sin ^α/₂ + ½ l_ac sin ^α/₂ = ½ l_a(b + c) sin ^α/₂

(рисунок сделайте самостоятельно). Из последнего равенства находим, что

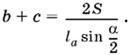
Подставляем в выражение для 2S полученное раньше:

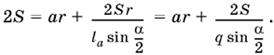
B последнем преобразовании мы учли условие задачи, согласно которому l_а = rq. Осталось ввести в рассмотрение радиус R описанной окружности. По условию R = prq. По теореме синусов

a = 2R sin α = 2prq sin α,

откуда r =^a/_{2pq sin α}. Полученное соотношение позволяет определить a из последнего выражения для 2S. B самом деле, после подстановки получим

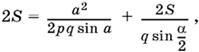
откуда после несложных преобразований найдем a.

Ответ.

1.9. B треугольнике ABC (рис. P.1.9) введем обозначения: ВМ = a₁, СМ = a₂, АN = b₁, СN = b₂. Так как ВО — биссектриса треугольника АВМ, то AB : ВМ = АО : ОМ = √3 : 1. Аналогично AB : АN = ВО : ОN = 1 : (√3 − 1). Итак,

Величины a₁ и b₁ можно выразить через стороны треугольника

a₁ = ^ac/_{b + с}, b₁ = ^bc/_{а + с}.

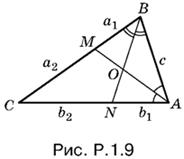
После подстановки в предыдущие два равенства мы получим два однородных выражения относительно a, b и с:

^{b + c}/_a = √3, ^{a + c}/_b = ½(√3 + 1),

из которых легко найти отношения a : b и с : b. Достаточно переписать эти равенства в виде

1 + ^с/_b = √3^a/_b, ^a/_b + ^с/_b = ½(√3 + 1).

Получим ^a/_b = ^√3/_c, ^с/_b = ½.

Таким образом, треугольник ABC подобен прямоугольному треугольнику с углами в ^π/₆ и ^π/₃·

Ответ. Углы А, B и С равны ^π/₃, ^π/₂, ^π/₆ соответственно.

1.10. Из треугольника MPA (рис. Р.1.10) находим MP = PA ctg α. Но PA = OA − OP = ^q/_{cos α} − p. Таким образом,

Находим MQ:

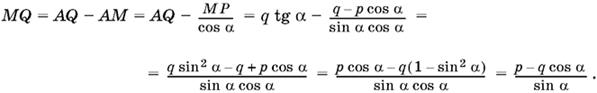
Полезно заметить, что MQ можно было не вычислять, поскольку выражение для MQ должно получиться из выражения для MP с помощью замены p на q, а q на p.

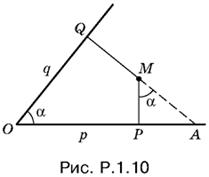
Ответ.

1.11. Пусть AP = 3, CR = 2√2 (рис. Р.1.11) Используя метод «сравнения площадей» для треугольника ABC, получим

3a = 2√2 c.

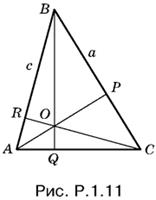
Так как а = ^BQ/_{sin C}, с = ^BQ/_{sin A}, то после сокращения на BQ получим

³/_{sin С} = ^2√2/_{sin А}^. (1)

По условию BQ = 6OQ. Найдем отрезок AQ из треугольников ABQ и AOQ соответственно:

AQ = BQ ctg А = 6OQ ctg А, AQ = OQ ctg ∠OAQ,

где ∠OAQ = ^π/₂ − С. Приравнивая эти два выражения, получим второе уравнение, связывающее углы треугольника:

6 ctg А ctg С = 1. (2)

Остается решить систему из уравнений (1) и (2). Для этого возведем уравнение (1) в квадрат и воспользуемся формулой

Получим

9(1 + ctg² С) = 8(1 + ctg² А). (1′)

Из уравнения (2) следует, что

(2′)

подставляя значение ctg² С в уравнение (1'), после несложных преобразований придем к биквадратному уравнению относительно ctg А:

32 ctg⁴ А − 4 ctg² А − 1 = 0. (3)

Так как треугольник ABC по условию остроугольный, то нас интересуют лишь положительные корни уравнения (3). Легко убедиться, что оно имеет единственный положительный корень ctg А = ½. Подставляя в (2), найдем ctg С = ⅓. Теперь можно найти площадь данного треугольника:

S_ABC = ½AP · a,

где АР = 3. Величину а найдем из треугольника BRC:

Ответ. 6 см².

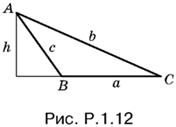
1.12. Поскольку B − С = ^π/₂, угол B — тупой (рис. P.1.12).

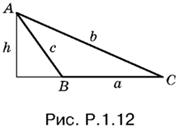
Так как

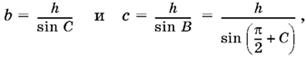
то соотношение b + с = k можно переписать так:

откуда

h(sin С + cos С) = k sin С cos С.

Возведем последнее уравнение относительно sin 2 С. Корни этого уравнения

Если мы возьмем перед корнем знак минус, то получим sin 2С < 0, чего быть не может, так как угол С острый, следовательно, 0 < 2С < π.

Остается

B правой части стоит положительное число. Чтобы можно было найти С, это число не должно превышать единицу, т. е.

Неравенство можно переписать так:

При возведении в квадрат необходимо добавить ограничение k² − 2h² ≥ 0. Получим систему

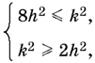
решением которой будет k ≥ 2√2 h, так как k и h по условию положительны.

Ответ.

1.13. Способ 1. После того как из точки О опущены перпендикуляры длины x, y и z на стороны а, b и с соответственно (рис. P.1.13, а), можно записать

2S = ax + by + cz.

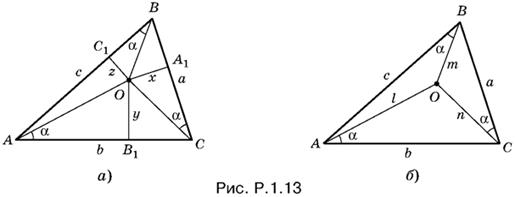
С одной стороны, АО = ^y/_{sin α}, а с другой стороны

Таким образом,

После простых преобразований получим

(y² − z²) cosec² α = c² − 2cz ctg α,

(x² − y²) cosec² α = b² − 2by ctg α,

(z² − x²) cosec² α = a² − 2ax ctg α,

где последние два уравнения выведены аналогично первому из рассмотренных отрезков CO и BO. Сложив все три уравнения, получим в левой части нуль, а в правой выражение, в которое входит S:

0 = (a² + b² + c²) − 2(ax + by + cz) ctg α.

Таким образом,

Способ 2. Так как площадь треугольника ABC равна сумме площадей трех треугольников, на которые треугольник ABC разбивается точкой O (рис. P.1.1З, б), то

S = ½ sin α (an + bl + cm).

Записав теорему косинусов для каждого из треугольников AOB, BOC, COA, получим

2an cos α = a² + n² − m²,

2bl cos α = b² + l² − n²,

2cm cos α = c² + m² − l².

Сложим три последних равенства:

2 cos α (an + bl + cm) = a² + b² + c².

Используя полученное ранее выражение для S, исключим an + bl + cm.

Ответ.

1.14. По условию CD = BC − AC (рис. P.1.14).

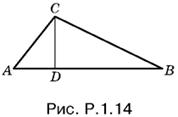
Так как

AC = ^CD/_{sin A}, BC = ^CD/_{sin B},

то

CD (¹/_{sin B} − ¹/_{sin A}) = CD

или

sin А − sin B = sin A sin B.

Последнее уравнение можно переписать так:

4 sin ^{A − B}/₂ cos ^{A + B}/₂ = cos (А − B) − cos (А + B).

Так как А − B = φ, то после замены

cos (А + B) = 2 cos² ^{A + B}/₂ − 1

приходим к уравнению относительно y = cos ^{A + B}/₂:

y² + 2 sin ^φ/₂ y − cos² ^φ/₂ = 0.

Из его корней

y_{1, 2} = ±1 − sin ^φ/₂

годится только первый, т. е.

cos ^{A + B}/₂ = 1 − sin ^φ/₂.

Задача имеет решение при 0 < φ < π.

Остается решить систему

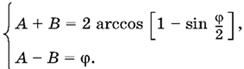
Ответ. А = arccos [1 − sin ^φ/₂] + ^φ/₂,

B = arccos [1 − sin ^φ/₂] − ^φ/₂

С = π − А − B.

1.15. Площадь S треугольника ABC (рис. P.1.15) может быть записана с помощью биссектрисы l следующим образом:

S = ½(а + b)l sin ^С/₂.

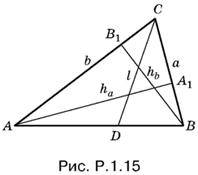
Теперь приравняем три выражения для 2S:

аh_а = bh_b = (а + b)l sin ^С/₂.

Исключая а, получим

откуда

Задача имеет решение, если

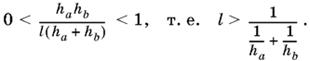
B правой части стоит величина, равная половине среднего гармонического длин h_а и h_b.

Ответ.

если длина биссектрисы больше среднего гармонического длин h_а и h_b.

1.16. Так как ОС и OB (рис. P.1.16) — биссектрисы соответствующих углов треугольника ABC, то

∠COB = π − (∠OCB + ∠OBC) = π − ^{B + C}/₂.

Но B + С = π − А = π − α. Следовательно, ∠COB = ^π/₂ + ^α/₂.

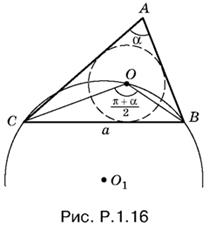
Применяя теорему синусов, получим

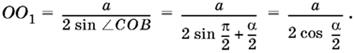
Ответ.

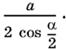
1.17. Проведем через центр О₁ (рис. P.1.17) вписанной в треугольник ABC окружности прямую, параллельную AC и пересекающую медиану AE в точке О. Докажем, что О — точка пересечения медиан треугольника ABC.

С помощью сравнения площадей получим (а + d)BD = rP, где

P = а + (а + d) + (а + 2d) = 3(а + d),

откуда BD = 3r.

Так как AE — медиана, то из подобия треугольников BDC и EFC следует, что

EF = ½ D = ³/₂ r.

Из подобия треугольников AOC и AEF получаем АО : AE = OG : EF = 2 : 3.

Следовательно, АО : ОЕ = 2 : 1 и О — точка пересечения медиан.

1.18. Площадь треугольника ABC (рис. P.1.18), с одной стороны, равна ½ h_аа = 2kr², а с другой стороны, равна pr. Следовательно, p = 2kr.

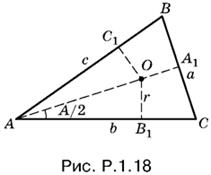
Так как АВ₁ = АС₁ (касательные к одной окружности) и аналогично BC₁ = ВА₁, СВ₁ = СА₁, то СВ₁ + BC₁ = СА₁ + ВА₁ = а, АВ₁ + СВ₁ + BC₁ = p и АВ₁ = p − а = 2kr − kr = kr. Теперь можно вычислить

tg ^А/₂ = ^r/_kr = ¹/_k.

Чтобы найти стороны b и с, определим величины b + с и bc. Величина b + с определяется просто:

b + с = 2p − а = 3kr.

Чтобы найти bc, вспомним, что площадь треугольника ABC, равная 2kr², может быть записана в виде ½ bc sin А, где sin А = ^2k/_{1 + k²} (по формуле универсальной подстановки). Таким образом, bc = 2r²(1 + k²).

Решая систему уравнений

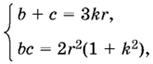
найдем

или наоборот

Задача имеет решение при k > 2√2.

Ответ.

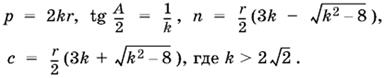
1.19. Так как углы С, А, B треугольника ABC образуют геометрическую прогрессию со знаменателем 2, то А = 2С, B = 4С (рис. P. 1.19). Точка О — центр вписанной окружности, т. е. OK и OL являются отрезками соответствующих биссектрис.

Вычислим углы треугольника OLK. Угол KOL равен углу BOA треугольника BOA, в котором два угла уже известны: угол при вершине А равен С, а угол при вершине B равен 2С. Следовательно, угол BOA = π − 3С. Но по условию π = А + B + С = 7С, т. е. угол BOA, а следовательно, и угол LOK равны 4С.

Рассмотрим далее треугольник EKC. Угол при вершине E в этом треугольнике (равный углу AEO из треугольника AEO) вместе с углом OAE, равным С, образуют угол LOK, равный 4С. Таким образом, угол KEC равен 3С. Угол ECK равен половине угла ECM, который вместе с углом С образуют π, т. е. 7С. Следовательно, угол ECK равен 3С. Найденные два угла, каждый из которых равен 3С, позволяют найти третий: угол OKL равен С.

Таким образом, подобие треугольников ABC и ОLK доказано.

1.20. Сумма всех углов треугольника равна 7А. Поэтому

B силу теоремы синусов

Соотношение, которое нужно доказать, эквивалентно такому:

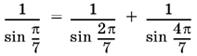
или

Преобразуем левую часть:

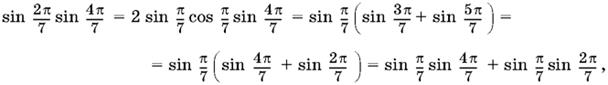
что и доказывает наше соотношение.

1.21. Проведем AL параллельно BC (рис. P.1.21).

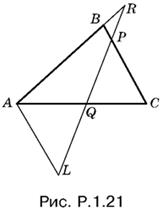
Из подобия треугольников RAL и RBP следует, что

Из подобия треугольников AQL и CQP:

Подставляя значение AL в отношение, полученное раньше, придем к равенству

что и требовалось доказать.

1.22. Пусть AE — высота треугольника, опущенная на BC (рис. P.1.22). Тогда все участвующие в левой части равенства величины можно выразить через AE и длины отрезков, лежащих на BC. При этом следует стремиться связать каждый отрезок с точкой 1. Получим

AB² = BE² + AE² = (BD + DE)² + AE².

AC² = CE² + AE² = (CD − DE)² + AE².

AD² = DE² + AE.

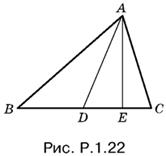
Воспользовавшись полученными соотношениями, составим сумму

AB² · DC + AC² · BD − AD² · BC.

Раскрыв скобки и приведя подобные члены, получим

(DE² + AE²)(DC + BD − BC) + DC · BD² + BD · DC².

Так как DC + BD = BC, то остается

DC · BD² + BD · DC² = (BD + DC)DC · BD = BC · DC · BD,

что и требовалось доказать.

1.23. Проведем CE и AD параллельно BQ, а отрезки AP и CR продолжим до пересечения с ними (рис. P.1.23).

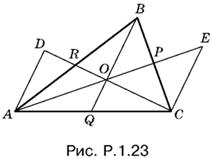
Рассмотрим образовавшиеся в результате подобные треугольники. Так как отрезки AD и OQ параллельны, то

Из подобия треугольников ADO и OEC следует, что

. Итак,

.

Воспользовавшись двумя парами подобных треугольников: EPC и OBP, ADR и RBO, мы можем записать

Следовательно,

1.24. Треугольник ABC и три треугольника, образовавшихся внутри него (рис. P.1.24), подобны.

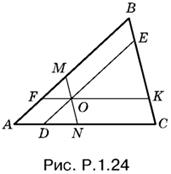
Поэтому

Следовательно,

1.25. Обозначим угол AOD (рис. P.1.25) через α. Так как углы AOB и BOC равны 120°, то углы BOF и COE равны соответственно 60° − α и 60° + α. Составим сумму

AD² + CE² + BF² = R² sin² α + R² sin² (60° + α) + R² sin² (60° − α).

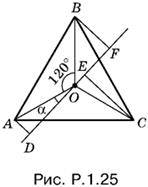
После понижения степени получим

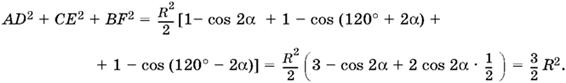
Тем самым доказано, что эта величина не зависит от положения прямой на плоскости.

1.26. По теореме косинусов

с² = а² + b² − 2ab cos С = 7,

откуда с = √7. По теореме синусов

Угол AOB (рис. P.1.26) центральный, а угол ACB вписанный. У них общая дуга, следовательно, угол AOB равен 120°.

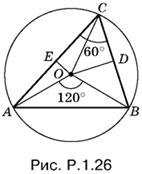
Применим теперь теорему синусов к треугольнику AOB:

Оставшиеся величины R_AOC и R_BOC можно найти по формуле R = ^abc/_4S.

Площади каждого из этих треугольников проще вычислить, если найти их высоты, опущенные из точки О:

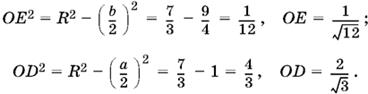
Таким образом, площади треугольников AOC и BOC равны

соответственно, а радиусы окружностей, описанных около этих треугольников, равны ⁷/_√3 и ⁷/_4√3 соответственно.

Ответ.

1.27. По теореме косинусов и в силу равенства а² = с(b + с) получим b² + с² − 2bc cos А = c(b + с), откуда

cos А = ^{b − c}/_2c.

Данное в условии равенство можно записать так: с² = а² − bc, и сравнить его с теоремой косинусов для угла С. Получим

cos С = ^{b + c}/_2a.

Нам нужно доказать, что угол А вдвое больше угла С. Вычислим для этого cos 2С и сравним с cos А:

B выражение для cos А, которое мы получили раньше, сторона а не входит. Поэтому заменим в правой части полученной формулы а² на bc + с². Получим

т. е. cos А = cos 2С. Так как cos С = ^{b + c}/_2a > 0, то угол С острый. Углы А и 2С лежат между 0 и π, т. е. в интервале монотонности косинуса. Таким образом, из равенства косинусов следует равенство углов А = 2С.

1.28. Центр О вписанный окружности лежит на пересечении биссектрис (рисунок сделайте самостоятельно). Поэтому

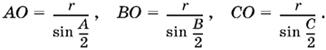
Подставляя в данное соотношение OA² = OB · OC, получим

Применив к правой части формулу преобразования произведения синусов в сумму, приведем равенство к виду

Заметив, что B + С = π − А, получим

cos ^{B − C}/₂ = 2 sin² ^А/₂ + sin ^А/₂,

что и требовалось доказать.

1.29. По условию S = а² − b² − с² + 2bc. С другой стороны, S = ½с sin А. Сравнивая эти выражения, получим а² − b² − с² + 2bc = ½ bc sin А.

Воспользуемся теоремой косинусов и заменим а² на b² + с² − 2bc cos А. После приведения подобных и сокращения на bc останется тригонометрическое уравнение

½ sin А = −2 cos А + 2,

которое можно переписать так:

sin ^А/₂ cos ^А/₂ = 4 sin² ^А/₂.

Так как А — угол треугольника, то А лежит в первой четверти и sin ^А/₂ ≠ 0. Наше уравнение принимает вид tg ^А/₂ = ¼.

Ответ. А = 2arctg ¼.

1.30. Пусть О₁, О₂, О₃ — центры квадратов, построенных на сторонах треугольника ABC (рис. P.1.30). Опустим из них перпендикуляры на стороны. Проведем средние линии DE и KE. На отрезках О₂K и KE построим параллелограмм KELO₂.

Рассмотрим четырехугольники О₁EDO₃ и BELO₂. При повороте около точки E одного из них на 90° он совпадает с другим (убедитесь в равенстве сторон и углов самостоятельно). Следовательно, отрезки О₁О₃ и ВО₂ равны, что и требовалось доказать.

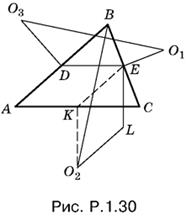
1.31. Достроим треугольник ABC до параллелограмма так, чтобы сторона AB была диагональю параллелограмма (рис. P.1.31).

Проведем BD₁ || AD. Точку пересечения BD₁ с диагональю CC₁ параллелограмма обозначим через M₁. Треугольники MDC и M₁BC подобны. Так как MF = ^CF/₄, то MC : MM₁ = 3 : 2. Следовательно, MD : M₁B = 3 : 5. Так как M₁B = AM, то AM : MD = 5 : 3.

Площадь треугольника AFM в восемь раз меньше площади треугольника ABC, т. е. равна 8 . Высота треугольника AFM (F — середина AB), опущенная из вершины F, в два раза меньше высоты треугольника ABD, опущенной из вершины B. Так как AM : AD = 5 : 8, то площадь треугольника AFM относится к площади треугольника ABD как 5 относится к 2 · 8, т. е. как 5 : 16.

Зная, что площадь треугольника AFM равна ⅛, можно теперь найти и площадь треугольника ABD.

Ответ. ²/₅.

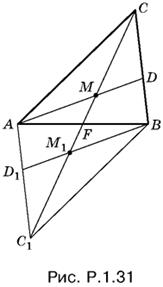
1.32. Способ 1. Пусть R — радиус окружности, а α, β и γ − вписанные углы, опирающиеся соответственно на стороны AB, BC и AD (рис. P.1.32). Углы, опирающиеся на одну и ту же дугу, равны (это отмечено на рисунке). Углы DBC и DAC тоже равны, и их нетрудно вычислить: ∠ DBC = ∠ DAC = π − (α + β + γ). По теореме синусов

AB = 2R sin α, BC = 2R sin β, DC = 2R sin (α + β + γ), AD = 2R sin γ.

Таким образом,

AB · DC + AD · BC = 4R² [sin α sin(α + β + γ) + sin β sin γ] = 2R² [cos(β + γ) − cos(2α + β + γ) + cos(β − γ) − cos(γ + β)] = 2R² [cos (β − γ) − cos(2α + β + γ)].

Так как

AC = 2R sin (α + β), BD = 2R sin (α + γ),

то

AC · BD = 4R² sin (α + β) sin (α + γ) = 2R² [cos (β − γ) − cos (2α + β + γ)].

Итак,

AB · DC + AD · BC = AC · BD.

Способ 2. Введем обозначения: AB = а, BC = b, CD = с, DA = d, AC = e, BD = f. Нужно доказать, что ac + bd = ef. Выберем на диагонали AC точку E так, чтобы угол CBE был равен γ. Тогда треугольники CBE и DBA подобны. Поэтому EC : b = d : f.

Из подобия треугольников ABE и DBC (углы ABE и DBC равны как равносоставленные) получаем AE : а = с : f. Определим из первого соотношения EC, а из второго AE и сложим эти два равенства:

откуда ас + bd = ef, что и требовалось доказать.

1.33. Продолжим боковые стороны AB и CD трапеции (рис. P.1.33) до пересечения в точке S. Если через S и M (где M — середина BC) провести прямую, то она пересечет AD в точке N, которая является серединой AD.

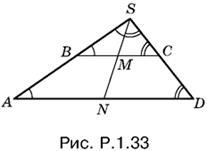
Из подобия треугольников BSM и ASN имеем

откуда

Так как по условию MN = AN − BM, то BM = SM и треугольник SMB равнобедренный. Аналогично доказывается, что треугольник SMC также равнобедренный. Следовательно, угол SMC равен удвоенному углу А, а угол SMB — удвоенному углу D (по свойству внешнего угла треугольника). Но оба этих угла SMB и SMC образуют развернутый угол. Следовательно, сумма углов А и D равна 90°.

1.34. Пусть AB = а, MR = x (рис. P.1.34).

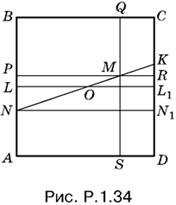
Выразим через а и x длины отрезков MQ, MS и MP. Ясно, что для этого достаточно найти длину отрезка QM, поскольку MS = а − QM, а MP = а − x. Так как QM = CR = CK + KR, то вычислим CK и KR. По условию AN = ^а/₃, а потому (треугольники OLN и OL₁K равны) CK = ^а/₃. Чтобы найти KR, рассмотрим подобные треугольники MKR и NKN₁:

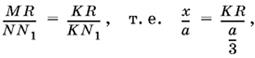
откуда KR = ^x/₃, а QM = ^а/₃ + ^x/₃. Остается убедиться в том, что числа а − x, ^{2a − x}/₃, ^{а + x}/₃, x образуют арифметическую прогрессию с разностью ^{2x − a}/₃.

1.35. Пусть CE = x (рис. P.1.35).

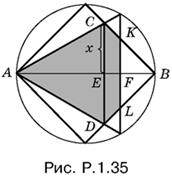
Выразим через x отрезок AE из треугольника ACE, в котором угол CAE равен 30°: AE = x√3 . С другой стороны, AE = AB − BE, а так как BE = CE = x, то AE = 2 − x. Итак, 2 − x = x√3 , откуда x = √3 − 1.

Заметим, что KF = FB = ½; площадь искомой фигуры равна

S_ACD + S_BCD − S_BKL = 2S_ACB − S_BKL.

Ответ. 2√3 − ⁹/₄ .

1.36. Углы при нижнем основании трапеции и основании треугольника равны. Обозначим их через α. Тогда угол BAO равен углу ABO, т. е. равен 90° − α (рис. P.1.36). Поэтому угол OAD равен 2α − 90°. Так как треугольник MNO равнобедренный (MO = NO), то угол MNO равен α, а угол NOE равен 90° − (180° − 2α), т. е. равен 2α − 90°.

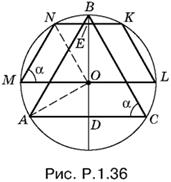
Треугольники ONE и AOD равны (по гипотенузе и острому углу). Следовательно, OE = AD. Кроме того, MO = OB, как два радиуса, и NE = OD, как стороны равных треугольников. Это означает, что BD = l.

По условию AD · BD = S, следовательно, OE = AD = ^S/_l.

Ответ. ^S/_l.

1.37. Из подобия треугольников AOD и BOC (рис. P.1.37) находим, что ^MO/_NO = p, т. е. ^MN/_NO = p + 1.

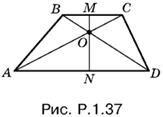
Отношение площадей трапеции и треугольника AOD можно записать в виде

Ответ. (p + 1)².

1.38. Пусть R — радиус окружности, n — число сторон первого многоугольника, x — периметр третьего.

Периметры первого и второго многоугольников равны соответственно

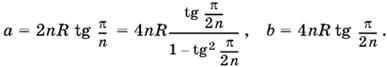
Периметр третьего равен

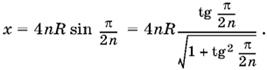
Сравнивая первые два выражения, найдем, что 1 − tg²^π/_2n = ^b/_a. Следовательно,

Ответ.

1.39. Если точки О и M расположены так, как показано на рис. Р.1.39, а, то NM > KL, так как хорда NM ближе к центру окружности. Но NM < а, а KL = 2а. Получаем а < 2а, что невозможно. Следовательно, фигуры расположены так, как показано на рис. Р.1.39, б.

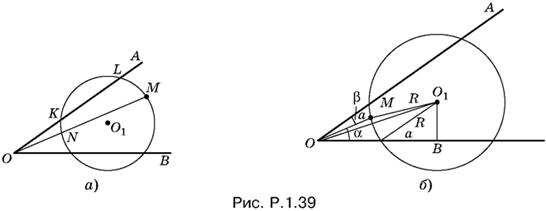
Центр рассматриваемой окружности лежит на биссектрисе угла AOB, так как точка О₁ равноудалена от лучей AO и OB.

Предположим для определенности, что угол α больше угла β. Треугольник OMO₁, в котором сторона OM равна а, сторона MO₁ равна R, а ОО₁ легко выражается через R, позволяет составить уравнение для определения R. B самом деле, угол MOO₁ равен α − ^{α + β}/₂ = ^{α − β}/₂. Следовательно, по теореме косинусов

R² = а² + ОО₁² − 2а · ОО₁ · cos ^{α − β}/₂.

Из треугольника О₁ОВ находим

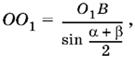
а так как

то

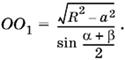
После подстановки уравнение относительно R выглядит следующим образом:

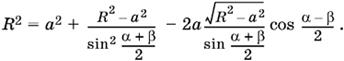
Заменим

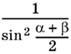
на

и после несложный упрощений

получим

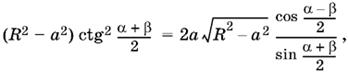
откуда

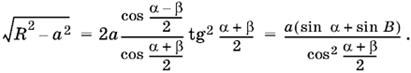
Ответ.

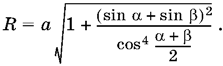
1.40. Запишем отношение площадей данных прямоугольных треугольников (рис. P.1.40):

Кроме того, AD · AB = AE · AC. Найдем отсюда AO и подставим в предыдущее равенство; получим

Обозначим углы ADC и AEB, опирающиеся на дугу BC, через φ:

Следовательно, дуга BC равна

Угол А прямой и измеряется полуразностью высекаемых им на окружности дуг (2π − ∪DE) и BC:

^π/₂ = ^{(2π − ∪DE) − ∪BC}/₂, т.E. ^π/₂ = ½(∪DE + ∪BC).

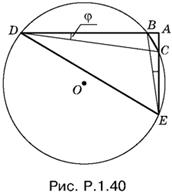
Отсюда найдем величину дуги DE, которая равна

Ответ.

1.41. Введем обозначения, указанные на рис. P.1.41. B треугольнике AOO₁:

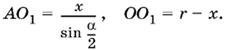
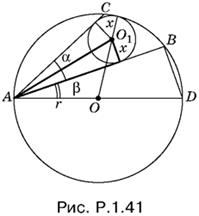
Чтобы применить к этому треугольнику теорему косинусов, обозначим угол BAD через β. Из треугольника ABD:

Следовательно, по теореме косинусов для треугольника АОО₁:

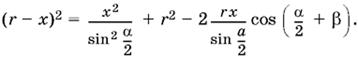
Раскроем скобки и воспользуемся формулой косинуса суммы. После упрощения получим искомый радиус.

Ответ.

1.42. Обозначим сторону квадрата через а. Тогда (см. рис. P.1.42)

Перед корнем выбраны два знака, так как искомый квадрат может быть расположен либо так, как показано на рис. P.1.42, а, либо так, как показано на рис. P.1.42, б. B первом случае нужно взять знак плюс, а во втором — минус.

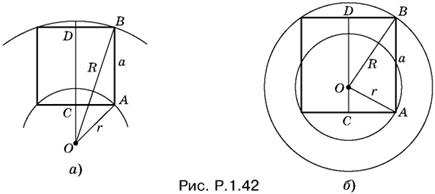
С другой стороны, из треугольника OBD находим

Получаем уравнение

После простых преобразований и повторного возведения в квадрат получаем уравнение

2a⁴ − 2a²(R² + r²) + (R² − r²)² = 0,

в котором исчезло различие между случаями, изображенными на рис. P.1.42, а, б. Из последнего уравнения имеем

или

Из первого выражения для а² видно, что оба значения положительны, если неотрицательно подкоренное выражение. Так как по условию R > r, то получаем

и окончательно

Ответ.

Задача имеет решение при 1 < ^R/_r ≤ 1 + √2. Если же ^R/_r = 1 + √2, то задача имеет единственное решение

1.43. Так как OE² = R² − x² и OF = ^R/₂ (рис. P.1.43), то

С другой стороны, EF = 2x. Получаем уравнение

R² − x² = (^R/₂ + 2x)²,

решая которое найдем половину стороны квадрата x = ³/₂ .

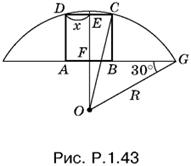
Ответ. 3.

1.44. Введем обозначения, указанные на рис. P.1.44. Так как меньшая окружность вписана в угол ADC, то ее центр О₁ лежит на биссектрисе этого угла.

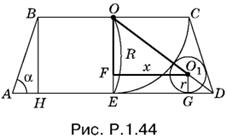
Из треугольника ОО₁F имеем ОО²₁ = OF² + FO²₁, т. е.

(R + r)² = (R − r)² + x². (4)

Из треугольника АВН: АН = ВН ctg α = R ctg α, т. е.

а = 2R + 2Rctg α. (5)

Из треугольника O₁GD:

r = (^a/₂ − x)tg ^α/₂. (6)

Из уравнения (4) находим 4Rr = x², или 2√R √r = x, и подставляем в уравнение (6). Получим

2r + 4√R √r tg ^α/₂ − a tg ^α/₂ = 0,

или, проще,

2 ctg ^α/₂r + 4√R √r − a = 0.

Мы пока не будем выражать R через а и α, а, наоборот, заменим а его выражением через R и α. Это удобнее, так как квадратное уравнение таково, что впоследствии √R можно будет вынести за скобки:

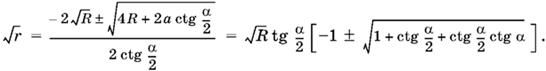
Знак минус перед корнем не имеет геометрического смысла. Если в подкоренном выражении воспользоваться формулой котангенса двойного угла, то

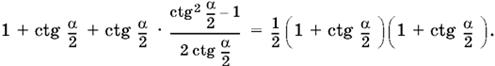
Следовательно,

Итак,

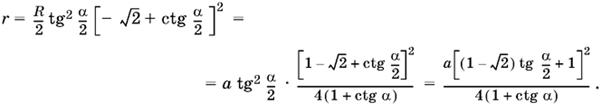
Ответ.

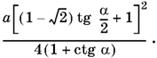
1.45. Рассмотрим вначале случай, когда диаметр CD разбивает фигуру PQNM на две части. Докажем, что фигуры CQNK и OQ₁D равновелики (рис. P.1.45, а). Имеем

S_CKNQ = S_CDQ − S_KND,

где S_CDQ = S_COQ + S_QOD.

Итак, S_CKNQ = S_COQ + S_QOD − S_KND.

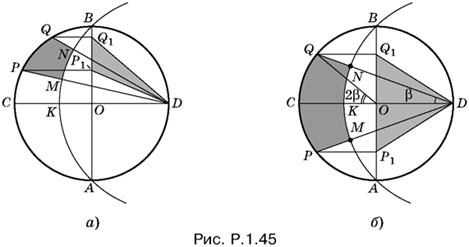
Если радиус меньшей окружности равен r, то радиус большей равен r√2. Углы CDQ и COQ опираются на общую дугу CQ, причем один из них вписан в окружность, а другой является центральным. Следовательно, если угол CDQ равен β, то угол COQ равен 2β. Теперь мы можем вычислить площади секторов COQ и KDN:

Таким образом, S_COQ = S_KND. Тем самым доказано, что S_CKNQ = S_QOD. Поскольку треугольники QOD и Q₁OD равновелики (у них общее основание и общая высота), то

Аналогично доказывается равенство

, что и завершает доказательство для случая, когда точки P и Q лежат по разные стороны от CD.

Если точки P и Q лежат по одну сторону от диаметра (рис. P.1.45, б), то решение не меняется. Только в конце найденные площади придется не складывать, а вычитать.

1.46. Из треугольника OAK (рис. P.1.46)

OK² = R² − (^AB/₂)².

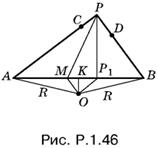
Так как KP₁ = AP₁ − ^AB/₂, то из треугольника OKP₁

По условию OP₁ = MP₁. Приравнивая два полученных выражения для OK² и заменяя ОР₁ на МР₁, найдем

Нам нужно вычислить длину отрезка MP. Чтобы воспользоваться прямоугольным треугольником MPP₁, в котором мы знаем длину МР₁, нужно вычислить PP₁. Так как треугольник APB прямоугольный, то

Теперь можно вычислить и МР:

Раскрывая скобки и приводя подобные члены, получим MP² = R².

Ответ. R.

1.47. Из треугольника AOC (рис. P.1.47) легко найти AC = ^4R/₅. Так как AC · СВ = МС · CN, то

откуда x = ^2R/₁₅.

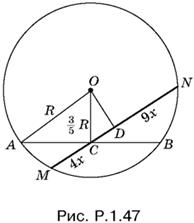
Проведем перпендикуляр OD к хорде MN. Так как MD = ^13x/₂, то

CD = MD − МС = ^5x/₂ = ^R/₃.

Косинус угла OCD равен синусу искомого угла NCB:

^CD/_OC = ^R/₃ : ^3R/₅ = ⁵/₉.

Ответ. arcsin ⁵/₉.

1.48. Соединим центры О₂ и O₁ рассматриваемых окружностей. Отрезок O₁О₂ равен x + ^R/₂ (рис. P.1.48).

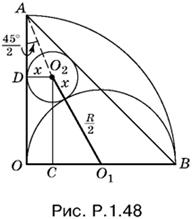
Центр О₂ лежит на биссектрисе угла OAB, равного 45°. Поэтому угол DAO₂ равен ^45°/₂. Это позволяет выразить через R и x отрезок DO:

DO = R − AD = R − x ctg ^45°/₂ = R − x ^{1 + cos 45°}/_{sin 45°} = R − x(√2 + 1).

Так как CO₁ = ^R/₂ − x, O₂С = DO = R − x(√2 + 1), а O₁O₂ = x + ^R/₂, то по теореме Пифагора для треугольника O₂CO₁ получим

(^R/₂ − x)² + [R − x(√2 + 1)]² = (^R/₂ + x)²,

или после преобразований

[R − x(√2 + 1)]² = 2Rx,

т. е.

Получили квадратное уравнение относительно √x. Решая его, найдем

Так как

то

(Второе значение √x не имеет смысла.)

Ответ. x = (3 − 2√2)R.

1.49. Соединим точки M и C (рис. P.1.49).

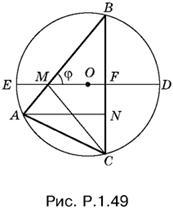
Так как диаметр ED перпендикулярен к BC, то точка N делит хорду BC пополам. Это означает, что треугольник МСВ равнобедренный. Обозначим МВ = МС = px. Угол АМС равен удвоенному углу МBC, т. е. π − 2φ. Из треугольника АМС по теореме косинусов имеем

AC² = АМ² + МС² − 2АМ · МС cos (π − 2φ) = x²(q² + р² + 2 pq cos 2φ),

а из треугольника ABC по теореме синусов

AC = 2R sin ^π/₂ − φ = 2R cos φ,

т. е.

АС² = 4R² cos² φ.

Приравнивая найденные выражения для АС², получим

Площадь треугольника ABC будем искать в виде S = ½AN · BC. Так как МВ = px, а МА = qx, то AB = (p + q)x. Из треугольника ABN находим AN = AB cos φ = (p + q)x cos φ. Сторону BC можно определить из треугольника MBF в котором сторона BF = ½BC:

BC = 2BF = 2MB sin φ = 2px sin φ.

Таким образом, S = p(p + q)x² sin φ cos φ = ½ p(p + q)x² sin 2φ, откуда

Ответ.

1.50. Стороны треугольника по условию равны а − d, а, а + d, где через а мы обозначили длину средней стороны. Тогда полупериметр p = ^3a/₂ и из формулы Герона получим уравнение относительно а:

Введем новую переменную

. Тогда получим

откуда

Далее найдем

Поскольку R = ^abc/_4S, то в нашем случае

Ответ.

1.51. Проведем PP₁ || AC и QQ₁ || AC (рис. P.1.51).

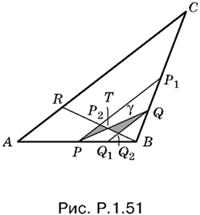
Пусть P₂ — точка пересечения PP₁ с BR, а Q₂ — точка пересечения QQ₁ с BR. По условию P — середина AB. Следовательно, Р₁ — середина BC, а Р₂ — середина BR. Аналогично Q — середина P₁B (так как по условию QB = ^BC/₄), Q₁ — середина PB, Q₂ — середина BP₂. Из подобия треугольников P₂TP и Q₂TQ (у них равны углы) следует, что P₂T : TQ₂ = PP₂ : QQ₂. Так как P₂P₁ = 4P₂P, а

, то QQ₂ = 2P₂P. Поэтому P₂T : TQ₂ = 1 : 2, а значит, и PT : TQ = 1 : 2.

Ответ. B отношении 1 : 2.

1.52. Способ 1. Соединим точки P и T (рис. P.1.52, а).

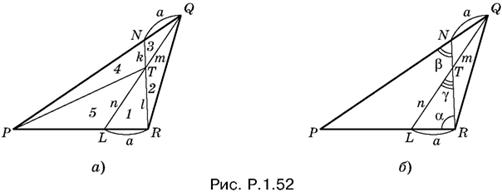
Пусть QN = RL = а, QT = m, TL = n, RT = l, TN = k. Обозначим треугольники, полученные из треугольника PQR: треугольник LTR — цифрой 1, треугольник RTQ — цифрой 2, треугольник QTN — цифрой 3, треугольник NTP — цифрой 4, треугольник PTL — цифрой 5, а их площади или площади образовавшихся из них фигур буквой S с соответствующими индексами.

Треугольники 1 и 1 + 5 имеют общую высоту. Аналогично треугольники 3 и 4. Поэтому

S₁ : S_{1 + 5} = а : PR, S₃ : S₄ = а : PN,

откуда

(7)

B треугольниках 1 и 3 углы при вершине T равны как вертикальные, т. е. S₁ : S₃ = (nl) : (mk). У треугольников 4 и 1 + 5 общая высота, соответствующая вершине P, т. е. S₄ : S_{1 + 5} = k : l. Остается найти PN : PR из (7).

Способ 2. Пусть QN = RL = а, QT = m, TL = n (рис. P.1.52, б). Обозначим угол NRP через α, угол PNR через β, а равные углы RTL и NTQ через γ.

Из треугольника PNR имеем

^PN/_PR = ^{sin α}/_{sin β}. (8)

Из треугольника NTQ имеем

^a/_m = ^{sin γ}/_{sin β}. (9)

Из треугольника LTR имеем

^a/_n = ^{sin γ}/_{sin α}. (10)

Разделим (10) на (9):

^m/_n = ^{sin β}/_{sin α}, т. е. в силу (8) ^PN/_PR = ⁿ/_m.

Ответ. n : т.

1.53. Так как ∠MO₁N = 60°, то MN сторона правильного вписанного в первую окружность шестиугольника. Ее длина равна радиусу первой окружности. На хорду MN (рис. P.1.53) опирается также вписанный в первую окружность ∠MO₂N, измеряемый половиной дуги MbN, которая равна 300°.

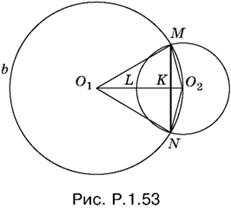
Поэтому центральный угол ∠MO₂N = 150°. Чтобы вычислить периметр фигуры MLNO₂, общей для обеих окружностей, нужно знать радиус второй окружности. Он равен длине любого из отрезков O₂L, O₂N и O₂М. Можно рассчитать из треугольника O₁MO₂ по теореме косинусов

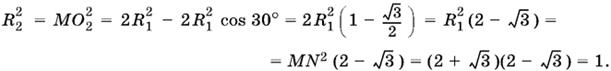
Теперь можно вычислить длины каждой из дуг MLN и MO₂N: дуга

B сумме получим

Ответ.

1.54. Пусть AB = а, BC = b, CD = с, DA = а, а опирающиеся на эти хорды углы равны соответственно α, β, γ, δ (рис. P.1.54).

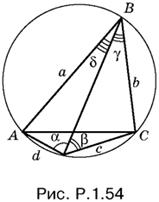
Тогда площадь S четырехугольника ABCD равна:

S = ½ab sin (γ + δ) + ½cd sin (α + β) = ½ sin (α + β)(ab + cd).

(Так как γ + δ = π − (α + β), то sin (α + β) = sin (α + β).)

По теореме синусов

а = 2R sin α = 2 sin α (так как R = 1),

b = 2 sin β, с = 2 sin γ, d = 2 sin δ.

Поэтому

S = sin (α + β)(2 sin α sin β + 2 sin γ sin δ) = sin (α + β) [cos (α − β) − cos (α + β) + cos (γ − δ) − cos (γ + δ)] =

(мы учли, что cos (α + β) = cos π − (γ + δ)) = − cos(γ + δ))

= 2 sin (α + β) cos ^{(α + γ) − (β + δ)}/₂ cos ^{(α + δ) − (β + γ)}/₂ =

(сумма четырех углов равна π, т. е. α + γ = π − (β + δ), α + δ = π − (β + γ))

= 2 sin (α + β) sin (β + δ) sin (β + γ).

Наибольшее значение S достигается при sin (β + δ) = 1, sin (β + γ) = 1 и при максимально возможном значении sin (α + β). Проверим, не противоречивы ли эти требования и реализуются ли они в реальности.

Из равенства синусов единице получаем, что β + δ = 90°, β + γ = 90°.

Отсюда δ = γ и ∠BCD = 180 ° − (β + γ) = 90°.

Таким образом, треугольник BCD — прямоугольный, a BD — диаметр окружности и BD = 2. Далее треугольник BAD равен треугольнику BCD (δ = γ и общая гипотенуза BD). Мы убедились, что условия sin (β + δ) = 1 и sin (β + γ) = 1 реализуемы. Остается еще одна степень свободы — выбор величины угла ABC, равного δ + γ, который по условию не превышает 45°. Чем больше угол δ + γ, тем больше sin (δ + γ) = sin (α + β). Поэтому наибольшему значению площади соответствует sin (α + β) = sin 45° = ^√2/₂, т. е. S = 2^√2/₂ = √2.

Ответ. √2.