Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003

Решения
Построения на плоскости

2.1. Осуществим параллельный перенос отрезка KL (рис. P.2.1), равного ширине реки, так, чтобы его точка L совпала с точкой B. Получим отрезок BE. Точку E соединим с точкой A, получим точку D, которую выберем за начало моста. Путь ADCB из A в B кратчайший, так как величина отрезка CD постоянна, а отрезки AD и CB спрямлены в AE.

2.2. На отрезках MP и PN (рис. P.2.2) построим сегменты, вмещающие угол 30°. B пересечении получим точку А. Соединим точку А с M и N, на AM и AN отложим отрезки длины а. Треугольник ABC искомый.

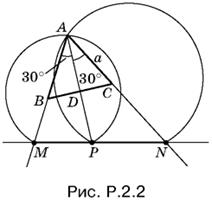
Задача имеет два решения. Одно изображено на рис. P.2.2, второе получится симметричным отражением первого от оси MN.

2.3. Пусть треугольник ABC искомый (рис. P.2.3). Отразим его от вертикальной оси, проходящей через середину BC. После этого треугольник CA₁A отразим от оси A₁A. B четырехугольнике C₁ABA₁ противоположные стороны AB и C₁A₁, а также A₁B и C₁A равны, т. е. он — параллелограмм с углом φ при вершине C₁ и углом π − φ при вершине А₁.

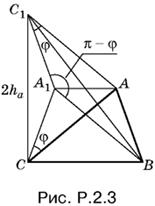
Так как точка С₁ отстоит от С на расстоянии 2h_а, то треугольник СС₁В легко построить. Остается найти точку А₁ как пересечение дуги сегмента, вмещающего угол π − φ и построенного на отрезке С₁В, с прямой, параллельной СВ и отстоящей от СВ на расстоянии h_а.

Задача имеет два симметричных решения, так как дуга сегмента может быть построена в любую сторону от С₁В. Построение возможно при любом соотношении между а, h_а и 0 < φ < π.

2.4. Пусть треугольник ABC — искомый и О — центр вписанной в него окружности. Если на отрезке АО = R (рис. P.2.4), как на диаметре, построить окружность, то она пересечет стороны AC и AB в точках F и E, являющихся серединами AC и AB соответственно. Отсюда построение: на отрезке АО = R строим, как на диаметре, окружность. Из точки А раствором циркуля, равным ^b/₂, делаем на окружности засечку в точке F. Продолжаем AF за точку F на расстояние ^b/₂ и получаем точку С. Из нее проводим дугу радиусом m_c.

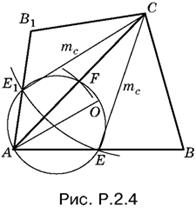
Задача имеет два решения: треугольник ABC и треугольник AB′С, если дуга ЕЕ′ пересекает окружность, построенную на AO; одно решение, если дуга касается окружности, и не имеет решения, если общих точек у дуги и окружности нет.

2.5. Так как углы OBO₁ и OCO₁ (рис. P.2.5) прямые, то вершины B и С треугольника лежат на окружности, построенной на отрезке ОО₁, как на диаметре. Центр этой окружности обозначим буквой Q.

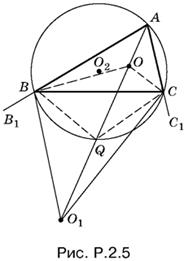
Угол BQC — центральный в той окружности, в которую угол BOC вписан (см. рисунок). Дуга, на которую опирается угол BOC, равна 2π − ∠BQC, а так как вписанный угол измеряется половиной дуги, на которую он опирается, то

∠ВОС = 2π − 2 ∠ВОС.

Остается найти угол ВОС:

∠ВОС = π − ^{B + C}/₂ = π − ^{π − A}/₂ = ^{π + A}/₂,

следовательно,

∠BQC = 2π − (π + А) = π − А.

Углы ВАС и BQC дают в сумме π; то же самое можно сказать об углах QBA и QCA, так как сумма всех углов четырехугольника равна 2π. Тем самым мы доказали, что точка Q лежит на окружности, описанной около треугольника ABC.

Построение можно провести следующим образом. Строим на отрезке ОО₁, как на диаметре, окружность с центром в точке Q. Радиусом О₂Q (О₂ — центр описанной окружности) проводим окружность с центром в точке О₂. B пересечении этих окружностей получим вершины B и С искомого треугольника.

Если точка О₂ лежит вне окружности радиуса, равного ¼ОО₁, с центром Q, то задача имеет единственное решение. B противном случае решения нет. (Докажите.)

2.6. Отбросим на время условие, в силу которого точка E лежит на BC, а остальные условия сохраним. Отложим на AB произвольный отрезок AF (рис. P.2.6), а на BC — отрезок CK = AF. Через точку K проведем прямую, параллельную AC, и из точки N раствором циркуля, равным AF, сделаем на этой прямой засечку.

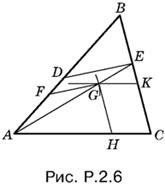
Фигура AFGH, где отрезок GH параллелен KC, будет подобна искомой с центром подобия в точке А. Строим вершину E, которая должна лежать на пересечении прямых BC и АG. Проводим DE параллельно FG.

Четырехугольник ADEC искомый. (Сделайте рисунок для случая, когда угол B тупой.)

Докажите, что в обоих случаях задача имеет единственное решение.

2.7. Проведем через точку M прямую AB так, чтобы ее отрезок, заключенный между сторонами угла, делился в точке M пополам. Для этого построим МС параллельно OA (рис. P.2.7, а) и отложим СВ = ОС. Так как СМ — средняя линия в треугольнике ОВА, то ВМ = МА.

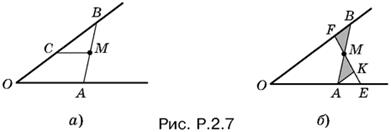
Итак, пусть AM = МВ (рис. P.2.7, б). Проведем произвольную прямую EF через точку M. Покажем, что площадь треугольника ОАВ меньше площади треугольника ОЕF. Проведем AK параллельно OB (если FM < ЕМ). Треугольники AMK и ВМF равны. Следовательно,

S_ОЕf = S_ОАМF + S_AMK + S_AEK > S_ОАМF + S_ВМF = S_ОАВ.

2.8. Вместо искомого треугольника ABC построим треугольник А₁АА₂, который получается из ABC так, как показано на рис. P.2.8 (А₁В = ВА, А₂С = СА).

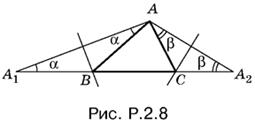
Угол А₁АА₂ этого треугольника равен α + β + А. Однако 2α = B, а 2β = С (по свойству внешних углов). Поэтому

α + β + А = ^{B + C}/₂ + A = ^{π − A}/₂ + A = ^{π + A}/₂.

Теперь в треугольнике А₁АА₂ известны основание А₁А₂ = 2p, высота, равная h_а, и угол при вершине, равный ^π/₂ + ^А/₂. Вершина А будет лежать на пересечении прямой, параллельной А₁А₂ и отстоящей от А₁А₂ на расстоянии h_а, и сегмента, построенного на отрезке А₁А₂ и вмещающего угол ^π/₂ + ^А/₂.

Вершины B и С лежат на пересечении А₁А₂ и перпендикуляров, проведенных через середины А₁А и А₂А.

Задача может иметь два симметричных решения, если высота меньше стрелки сегмента, одно решение, если они равны, и не имеет решений, если h_а больше стрелки сегмента.

2.9. Пусть P — искомая точка. Повернем треугольник АВР на 60° вокруг точки А. При этом точка P перейдет в точку Р₁, а точка B — в точку В₁ (рис. P.2.9).

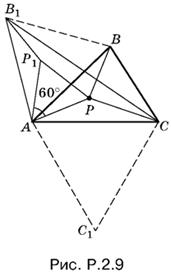
Так как угол Р₁АР равен 60° и АР₁ = АР, то треугольник Р₁АР правильный и АР = Р₁Р. Таким образом, В₁Р₁РС — ломаная, составленная из отрезков длины BP, АР и CP соответственно. Так как эта ломаная имеет закрепленные концы в точках В₁ и С, то ее длина будет наименьшей, если она выпрямится в отрезок В₁С.

Итак, точка P лежит на отрезке В₁С. Аналогично можно показать, что точка P лежит на отрезке С₁В, вершина С₁ которого получена поворотом AC вокруг А на 60°.

Отсюда простое построение. На отрезках AB и AC строим правильные треугольники АВ₁В и АС₁С, лежащие вне треугольника ABC. Искомая точка P будет лежать на пересечении прямых В₁С и С₁В.

2.10. Если треугольник ABC искомый (рис. P.2.10), то описанная около него окружность пересечется с биссектрисой CD в точке E, делящей дугу АЕВ пополам. Следовательно, точку E мы можем построить.

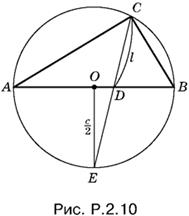
Вычислим отрезок DE. По свойству пересекающихся хорд в круге имеем CD · DE = AD · DB, или

l · DE = (АО + DO)(OB − OD),

т. е.

Так как OD² = DE² − ^c²/₄, то получаем уравнение относительно DE:

l · DE = ^c²/₂ − DE².

Решая его, найдем

(отрицательное значение для DE не имеет геометрического смысла).

Полученная формула позволяет легко построить отрезок DE, а следовательно, и СЕ.

Задача имеет два симметричных решения, если l < ^c/₂, одно решение, если l = ^c/₂, и не имеет решений, если l > ^c/₂.

2.11. B произвольно выбранных точках А и E прямой MN (рис. P.2.11) строим углы BAN и FEM, равные соответственно α и β.

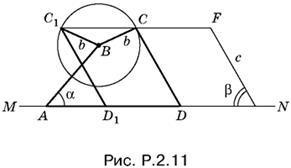
Откладываем AB = а и FE = с. Вершина С искомого четырехугольника лежит на окружности радиусом b с центром в точке B в на прямой CF параллельной MN. Если прямая пересекает окружность в двух точках С и С₁ (это происходит при b > |с sin β − а sin α|), то задача имеет два различных решения: ABCD и ABC₁D₁ (CD и C₁D₁ || EF), причем один четырехугольник будет самопересекающимся. При b = |с sin β − а sin α| решение единственно, а при b < |с sin β − а sin α| искомый четырехугольник не существует.

2.12. На отрезке ОМ (рис. P.2.12) строим треугольник OCM, сторона OC которого равна 2R, а сторона CM равна R. Точку пересечения OC с окружностью обозначим через B. Секущая AM — искомая.

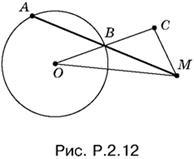
Задача имеет два решения, если MO < 3R, одно решение, если MO = 3R, и не имеет решений, если MO > 3R.

2.13. Соединим центры О и О₁ данных окружностей и построим на ОО₁, как на гипотенузе, прямоугольный треугольник ОЕО₁, один из катетов которого (EO₁) равен ^а/₂. Через точку M пересечения окружностей, лежащую по ту же сторону от ОО₁ что и построенный прямоугольный треугольник, проводим прямую, параллельную катету длины ^а/₂. Отрезок AB (рис. P.2.13) будет искомым.

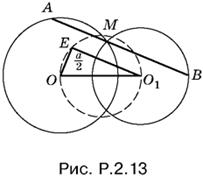
Задача имеет четыре решения, если ^а/₂ < ОО₁, два решения, если ^а/₂ = ОО₁, и не имеет решений, если ^а/₂ > ОО₁.

2.14. Проводим через точку M окружность, концентрическую данной. На этой окружности строим хорду длины а, проходящую через точку M. Задача может иметь два или одно решение (а < 2МО), а может и не иметь решения вовсе (а > 2МО).

2.15. Так как дуга AmB фиксирована, то известен и вписанный угол АМВ. Обозначим его через φ. Если отрезок PQ (рис. P.2.15) перенести параллельно в отрезок В₁В, то из точки P отрезок АВ₁ будет виден под углом φ. Таким образом, строим отрезок В₁В, равный а и параллельный CD; на отрезке АВ₁ строим сегмент, вмещающий угол φ, где φ — угол, измеряемый дугой AmB данной окружности. Искомая точка P есть точка пересечения или касания дуги этого сегмента с прямой CD.

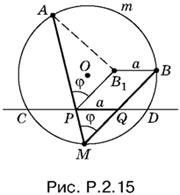
Задача может иметь два решения (сегмент, опирающийся на АВ₁, пересекает хорду CD), одно решение (этот сегмент касается хорды) и может не иметь решений вовсе (точек пересечения нет).

2.16. Пусть отрезок FD делится точкой M пополам (рис. P.2.16). Отразим точку B от точки M. Получим точку E. Отрезки FD и ЕВ можно рассматривать как диагонали параллелограмма.

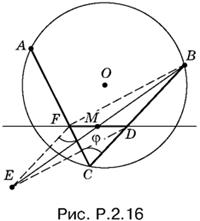
Заметим также, что угол АСВ известен, так как точки А и B зафиксированы на окружности; обозначим его через φ. Угол АFЕ равен π − φ. Следовательно, точка F обладает еще и тем свойством, что из нее отрезок AE виден под данным углом π − φ.

Итак, строим точку E, а на отрезке AE — сегмент, вмещающий угол π − φ. На пересечении дуги этого сегмента с данной прямой получим точку F.

Задача имеет единственное решение, если точки А и B лежат по одну сторону от данной прямой, и не имеет решений в остальных случаях.

2.17. Пусть прямая, проведенная через точки А и B, пересекает прямую PQ в точке С (рис. P.2.17), и пусть О — центр искомой окружности. Тогда СА · СВ = CD². Отрезки СА и СВ известны, отрезок CD — их среднее геометрическое и строится стандартным образом.

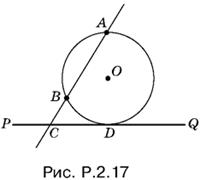
Если точки А и B лежат по одну сторону от PQ, то задача имеет два решения (отрезок CD можно отложить вправо и влево от точки С). Если AB и PQ параллельны, то задача имеет единственное решение, которое очевидно, но не может быть получено описанным способом. Когда точки А и P лежат по разные стороны PQ, задача не имеет решения.

2.18. Отрезки МВ и МА или их продолжения пересекают данную окружность в точках С и D (рис. P.2.18), которые являются основаниями высот треугольника АМВ, опущенных из его вершин А и B. Отрезок МР, проведенный через точку P пересечения AC и BD, будет искомым перпендикуляром.

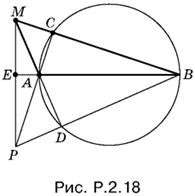
Задача имеет решение, если точка M не лежит на прямой AB.

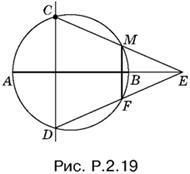
2.19. Предыдущая задача позволяет построить некоторый перпендикуляр к диаметру AB, пересекающий данную окружность в точках, которые мы обозначим буквами С и D (рис. P.2.19). Проведем прямую СМ; она пересечет диаметр AB (или его продолжение) в точке E. Проведем ED. B пересечении ED и данной окружности получим точку F; MF — искомый перпендикуляр.

2.20. Построим точку А₁ симметричную точке А относительно прямой l (рис. P.2.20). Для любой точки С на прямой l (в силу неравенства треугольника) справедливо соотношение

|AC − BC| = |А₁С − BC| ≤ А₁В.

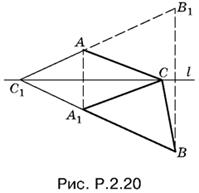
Величина |А₁С − BC| будет меняться в зависимости от положения точки С, и станет наибольшей, когда точка С займет положение С₁ (на пересечении прямых А₁B и l). Именно для этой точки треугольник СА₁В вырождается в отрезок С₁В, а неравенство треугольника превращается в равенство: |А₁С − BC| = А₁B. Из построения следует, что точка С единственная (если бы мы отражали от прямой l точку B, то пришли бы к той же точке С).

2.21. Две противоположные вершины искомого квадрата лежат, во-первых, на внешних полуокружностях, построенных на сторонах данного четырехугольника (рис. P.2.21), и, во-вторых, на диагонали квадрата, которая пересекает внутренние полуокружности в точках E и F, таких, что АF = FB = DE = EC = 45°.

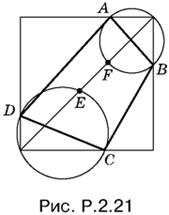
После проведенного анализа построение очевидно.

2.22. Выберем на глаз отрезок длины 1. Построим прямоугольный треугольник с катетами 1 и 1. Гипотенуза его равна √2. Далее возьмем катеты 1 и √2. Получим гипотенузу √3. Если же катеты равны √3 и 2, то гипотенуза равна √7. На сторонах острого угла А (для удобства) отложим AB = 1, АВ₁ = √7, AC = √7 (рис. P.2.22).

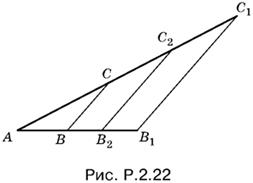
Соединим B и С, через В₁ проведем прямую, параллельную BC. Она пересечет AC в точке С₁. Из подобия треугольников ABC и АВ₁С₁ имеем AB : АВ₁ = AC : АС₁. Отсюда

Однако это 7 выбранных нами единиц, а не реальный отрезок длины 7, данный в условии задачи. Отложим АС₂ = 7. Это уже данный в условии отрезок. И проведем С₂В₂ || СВ. Отрезок АВ₂ = √7.

2.23. Так как длина искомого отрезка есть

а длина данного отрезка равна а, то рассмотрим только такие значения а, что одновременно

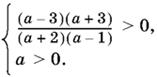
Решение этой системы есть два интервала: 0 < а < 1 и а > 3.

Пусть 0 < а < 1. Тогда удобнее записать длину искомого отрезка так:

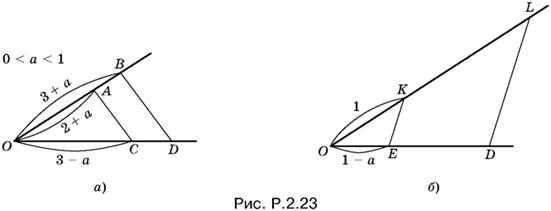
На одном луче угла отложим отрезки OA = 2 + а и OB = 3 + а, а на другом луче — отрезок ОС = 3 − а (рис. P.2.23, а). Соединим А и С, проведем BD || AC. Тогда

Осталось построить отрезок, длина которого равна ^OD/_{1 − а}. Для этого отложим на одном луче угла отрезки OD и ОЕ = 1 − а, а на другом луче отрезок OK = 1 (рис. P.2.23, б). Проведем DL || EK. Отрезок OL имеет искомую длину:

Осталось рассмотреть случай а > 3. Решение отличается только тем, что вместо отрезков длины 3 − а и 1 − а придется рассматривать отрезки длины а − 3 и а − 1.