Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Задачи
Геометрические задачи на плоскости
Обозначения: а, b, с — стороны треугольника; А, В, С — углы, лежащие против этих сторон, соответственно; mа — медиана стороны а; lA — биссектриса угла А; ha — высота, опущенная на сторону а; R — радиус описанной окружности; r — радиус вписанной окружности; P = 2р — периметр многоугольника.
Длиной биссектрисы внешнего угла А треугольника называется отрезок биссектрисы, заключенный между точкой А и точкой пересечения биссектрисы с продолжением стороны а.
Отношение площадей двух треугольников, имеющих общий угол, равно отношению произведений сторон, заключающих этот общий угол.
Имеет место формула, выражающая длину медианы треугольника через длины его сторон:
![]()
.
Если в многоугольник можно вписать окружность, то его площадь S = pr.
Площадь четырехугольника: S = ½ d1d2 sin α, где d1 и d2 — длины его диагоналей, а α — угол между ними.
При решении планиметрических задач приходится применять производные пропорции.
Если
![]()
.
Если
![]()
, то
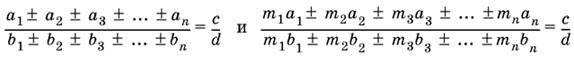
, где комбинация знаков берется любая, но одинаковая для числителя и знаменателя.
1.1. Вокруг правильного треугольника ABC описана окружность O радиусом R. Окружность O1 касается двух сторон AB и BC треугольника и окружности O. Найдите расстояние от центра окружности О1 до вершины А.
1.2. Высота равнобедренного треугольника с углом α при основании больше радиуса вписанного в него круга на m. Определите основание треугольника и радиус описанной окружности.
1.3. Докажите, что радиус окружности, делящей пополам стороны треугольника, вдвое меньше радиуса окружности, описанной около этого треугольника.
1.4. В треугольнике соединены основания биссектрис. Найдите отношение площади данного треугольника к площади образовавшегося треугольника, если стороны данного треугольника относятся как p : q : l.
1.5. Даны углы A, B, C треугольника ABC. Пусть окружность касается сторон BC, AC и AB треугольника соответственно в точках A1, B1, C1. Найдите отношение площади треугольника A1B1C1 к площади треугольника ABC.
1.6. Дан треугольник ABC, углы B и C которого относятся как 3 : 1, а биссектриса угла А делит площадь треугольника в отношении 2 : 1. Найдите углы треугольника.
1.7. Найдите длину l биссектрисы внешнего угла А треугольника, если даны его стороны b и c и угол А между ними (b ≠ c).
1.8. В треугольнике площади S, с острым углом α при вершине А биссектриса угла А в p раз меньше радиуса описанного и в q раз больше радиуса вписанного круга. Найдите сторону треугольника, лежащую против угла А.
1.9. В треугольнике ABC проведены биссектрисы AM и BN. Пусть O — точка их пересечения. Известно, что
AO : OM = √3 : 1, а BO : ON = 1 : (√3 − 1).
Найдите углы треугольника.
1.10. Внутри угла а взята точка M. Ее проекции P и Q на стороны угла удалены от вершины O угла на расстояния OP = p и OQ = q. Найдите расстояния MP и MQ от точки M до сторон угла.
1.11. В остроугольном треугольнике две высоты равны 3 и 2√2 см, а их точка пересечения делит третью высоту в отношении 5 : 1, считая от вершины треугольника. Найдите площадь треугольника.
1.12. В треугольнике ABC разность углов B и C равна π/2. Определите угол C, если известно, что сумма сторон b и c равна k, а высота, опущенная из вершины A, равна h.
1.13. В треугольнике ABC имеется точка O, такая, что углы ABO, ВСО и CAO равны α. Выразите ctg α через площадь треугольника и его стороны.
1.14. В треугольнике ABC дана разность φ углов A и В (φ = A − В > 0). Известно, что высота, опущенная из С на AB, равна BC − AC. Найдите углы треугольника.
1.15. Даны длины высот AA1 = ha и ВВ1 = hb треугольника ABC и длина CD = l биссектрисы угла С. Найдите угол С.
1.16. В треугольник с основанием а и противоположным углом α вписана окружность Через центр этой окружности и концы основания треугольника проведена вторая окружность Найдите ее радиус.
1.17. Докажите, что если длины сторон треугольника образуют арифметическую прогрессию, то центр окружности, вписанной в этот треугольник, и точка пересечения его медиан лежат на прямой, параллельной средней по длине стороне треугольника.
1.18. В треугольнике ABC радиус вписанной окружности равен r, сторона BC больше r в k раз, а высота, опущенная на эту сторону, больше r в 4 раза. Найдите полупериметр p, tg A/2 и стороны b и c.
1.19. Углы С, A, В треугольника ABC образуют геометрическую прогрессию со знаменателем 2. Пусть O — центр окружности, вписанной в треугольник ABC, K — центр вневписанной окружности, касающейся стороны AC, L — центр вневписанной окружности, касающейся стороны BC. Докажите, что треугольники ABC и OKL подобны.
1.20. В треугольнике ABC углы A, В и С образуют геометрическую прогрессию со знаменателем 2. Докажите, что
![]()
1.21. Докажите, что если P, Q, R — соответственно точки пересечения каждой из сторон BC, CA, AB (или их продолжений) треугольника ABC с некоторой прямой, то
![]()
(теорема Менелая).
1.22. Точка D находится на стороне BC треугольника ABC. Докажите, что
AB² · DC + AC² · BD − AD² · BC = BC · DC · BD
(теорема Стюарта).
1.23. На сторонах треугольника ABC взяты точки P, Q и R так, что три прямые AP, BQ и CR пересекаются в одной точке. Докажите, что
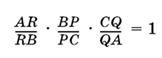
(теорема Чевы).
1.24. Через произвольную точку O, взятую внутри треугольника ABC, проведены прямые DE, FK, MN, параллельные соответственно AB, AC, BC, причем F и M лежат на AB, E и K — на BC, N и D — на AC. Докажите, что
![]()
1.25. Через центр O правильного треугольника ABC проведена произвольная прямая. Докажите, что сумма квадратов расстояний от вершин треугольника до этой прямой не зависит от выбора прямой.
1.26. Вокруг треугольника ABC, в котором а = 2, b = 3 и угол C = 60°, описана окружность. Определите радиусы окружностей, проходящих через две вершины треугольника и центр описанной окружности.
1.27. Стороны треугольника связаны соотношением а² = c(b + с). Докажите, что угол A вдвое больше угла C.
1.28. Пусть O — центр окружности, вписанной в треугольник ABC. Докажите, что если OA² = OB · OC, то
![]()
1.29. Площадь , треугольника ABC удовлетворяет соотношению S = а² − (b − с)². Найдите угол A.
1.30. На сторонах треугольника внешним образом построены квадраты. Докажите, что расстояние между центрами квадратов, построенных на боковых сторонах, равно расстоянию от центра квадрата, построенного на основании, до противоположной вершины треугольника.
1.31. В треугольнике ABC единичной площади проведен отрезок AD, пересекающий медиану CF в точке M, причем FM = ¼CF. Найдите площадь треугольника ABD.
1.32. Докажите, что произведение диагоналей вписанного четырехугольника равно сумме произведений противоположных сторон (теорема Птолемея).
1.33. Отрезок, соединяющий середины оснований трапеции, равен их полуразности. Найдите сумму углов при большем основании трапеции.
1.34. Через центр квадрата ABCD проведена прямая, пересекающая сторону AB в точке N, причем AN : NB = 1 : 2. На этой прямой взята произвольная точка M, лежащая внутри квадрата. Докажите, что расстояния от точки M до сторон квадрата AB, AD, BC и CD, взятые в названном порядке, образуют арифметическую прогрессию.
1.35. Квадрат и правильный треугольник, имеющие общую вершину, вписаны в окружность единичного радиуса. Найдите площадь, покрытую и квадратом и треугольником.
1.36. В окружность вписаны равнобедренный остроугольный треугольник площадью S, и трапеция так, что ее большее основание совпадает с диаметром окружности, а боковые стороны параллельны боковым сторонам треугольника. Средняя линия трапеции равна l. Найдите высоту трапеции.
1.37. Найдите отношение площади трапеции ABCD к площади треугольника AOD, где O —точка пересечения диагоналей трапеции, если известно, что
![]()
.
1.38. Два правильных многоугольника с периметрами a и b описаны около окружности, а третий правильный многоугольник вписан в эту окружность. Второй и третий многоугольники имеют каждый вдвое больше сторон, чем первый. Найдите периметр третьего многоугольника.
1.39. Внутри угла AOB, меньшего π, дана точка M, находящаяся на расстоянии а от вершины угла. Отрезок ОМ образует углы α и β со сторонами угла AOB. Найдите радиус R окружности, проходящей через M и отсекающей на сторонах угла AOB хорды, равные 2а.
1.40. Из внешней точки A проведены две взаимно перпендикулярные секущие ABD и ACE к окружности с центром O. Площади треугольников ABC и АDЕ относятся как m : n. Определите величины дуг BC и DЕ, каждая из которых меньше полуокружности.
1.41. Из точки А, лежащей на окружности радиуса r, проведены две хорды AC и AB. Эти хорды лежат по одну сторону от диаметра окружности, проходящего через точку А. Длина большей хорды равна b, а угол ВАС равен α. Найдите радиус окружности, которая касается хорд AB и AC и дуги BC.
1.42. Даны две концентрические окружности радиусов R и r (R > r). Найдите сторону квадрата, две вершины которого лежат на одной окружности, а две другие — на другой. При каком соотношении между радиусами данных окружностей решение задачи возможно и при каком соотношении задача имеет единственное решение?
1.43. В сегмент, дуга которого содержит 120°, вписан квадрат. Определите сторону квадрата, если радиус R круга равен 2 + √19 .
1.44. У равнобочной трапеции с бо́льшим основанием а и острым углом α высота вдвое меньше меньшего основания. На меньшем основании, как на диаметре, построена окружность. Найдите радиус окружности, касающейся построенной окружности, большего основания и боковой стороны.
1.45. AB и CD — два взаимно перпендикулярных диаметра окружности S1. С центром в точке D радиусом BD построена окружность S2. Из точки D проведены две прямые, пересекающие окружность S1 в точках P и Q и дугу AB окружности S2, заключенную внутри окружности S1, в точках M и N. Точки P и Q спроецированы на AB; P1 и Q1 соответственно — их проекции. Докажите, что фигура RMNQ равновелика треугольнику P1Q1D.
1.46. Через точку P, лежащую вне окружности с центром O и радиусом R, проходят две взаимно перпендикулярные секущие. Первая секущая пересекает окружность в точках А и С (точка С лежит между P и А), а вторая секущая — в точках В и D (D лежит между P и В). Пусть Р1 — проекция P на AB, а M — одна из точек пересечения AB с окружностью, центр которой Р1, а радиус Р1О. Найдите длину МР.
1.47. Найдите угол между двумя хордами, пересекающимися внутри окружности, если точка их пересечения удалена от центра окружности на 3/5 ее радиуса и делит одну хорду пополам, а другую — в отношении 4 : 9.
1.48. Дан сектор ОАВ (O — центр) с центральным углом в 90° и радиусом R. На отрезке ОВ, как на диаметре, построена полуокружность, лежащая внутри сектора. Найдите радиус окружности, касающейся этой полуокружности и отрезков ОА и AB.
1.49. В круге проведена хорда AB, пересекающая диаметр DE круга в точке M и наклоненная к нему под углом φ. Дано, что
![]()
, где p и q — известные числа. Из точки В проведена хорда BC, перпендикулярная к диаметру DE, и точка С соединена с точкой А. Найдите площадь треугольника ABC, если радиус круга равен R.
1.50. Площадь треугольника равна S, а длины его сторон образуют арифметическую прогрессию, разность которой равна d. Найдите радиус описанной окружности.
1.51. В треугольнике ABC точка P лежит на стороне AB и AB = 2АР, точка Q — на стороне BC и BC = 4BQ, точка R — на стороне AC и AC = 5АВ. Отрезки PQ и BR пересекаются в точке T. В каком отношении точка T делит отрезок PQ?
1.52. В треугольнике PQR на стороне PQ взята точка N а на стороне РR — точка L. Отрезки QL и RN пересекаются в точке T. Дано QN = RL, QT : TL = m : n. Найдите PN : PR.
1.53. Две окружности с центрами О1 и О2 пересекаются в точках M и N. Точка О2 лежит на первой окружности. Найдите периметр фигуры, являющейся пересечением данных окружностей, если
![]()
.
1.54. Найдите наибольшее возможное значение площади четырехугольника ABCD, если он вписан в окружность радиусом 1 и угол при вершине В меньше 45°.