Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Алгебраические преобразования
7.1.
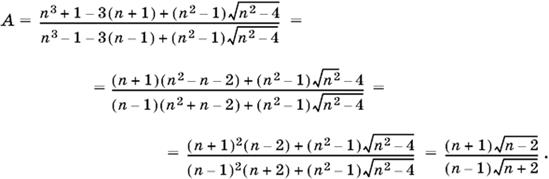
Ответ.
![]()
7.2. Перепишем данное выражение так:
![]()
Числитель второй дроби теперь легко разложить на множители. Со знаменателем дело обстоит несколько труднее. Однако в первую очередь нас интересует, делится ли знаменатель на 1 + x − x². Проверяем с помощью деления углом (проделайте это самостоятельно) и убеждаемся, что
x4 − x² − 2x − 1 = (1 + x − x²)(−x² − x − 1).
Таким образом,
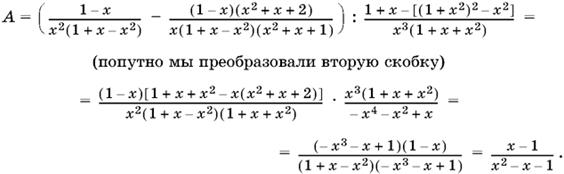
Ответ.
![]()
7.3. Приведем первые два слагаемых к общему знаменателю. Получим
![]()
где А и B — соответственно многочлены, входящие множителями в первое и во второе слагаемые.
Раскроем в числителе скобки и приведем подобные. После этого останется
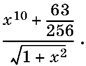
Преобразуем третье слагаемое:
![]()
Остается вычесть его из предыдущего результата.
Ответ.
![]()
это выражение положительно при x ≠ 0.
7.4. Домножив дробь на
![]()
получим
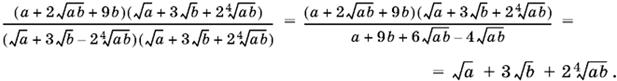
Остается вычесть 2√b и данное выражение примет вид
![]()
Ответ.
![]()
7.5. Вынесем за скобки
![]()
и воспользуемся выражением x через а:
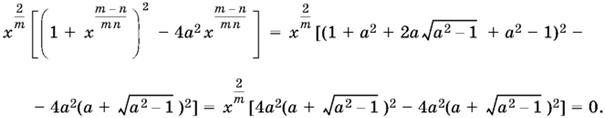
Ответ. 0.
7.6. Преобразуем данное выражение:
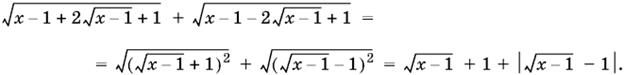
Так как 1 ≤ x ≤ 2, то 0 ≤ x − 1 ≤ 1 и, следовательно,
![]()
т. е.
![]()
Поэтому
![]()
Ответ. 2.
7.7. Так как 9 + 4√2 = (2√2 + 1)², то
![]()
Остается преобразовать
![]()
Если догадка, что
43 + 30√2 = 25 + 2 · 5 · 3√2 + 18 = (5 + 3√2)²,
кажется вам неестественной, то воспользуйтесь формулой сложного радикала
![]()
Ответ. 5 + 3√2.
7.8. Перепишем данное выражение в виде
(z² − y²)(xу + zu) + (x² − u²)(xу + zu) + (y² − z²)(xz + уu) + (x² − u²) × (xz + уu) = (z² − y²)(xу + zu − xz − уu) + (x² − u²)(xу + zu + xz + уu).
Так как
xу + zu − xz − уu = x(y − z) − u(y − z) = (y − z)(x − u),
xу + zu + xz + уu = (y + z)(x + u),
то получим
(z − y)(z + y)(y − z)(x − u) + (x − u)(x + u)(y + z)(x + u) = (x − u)(y + z)[−(y − z)² + (x + u)²].
Ответ. (x − u)(y + z)(x + u − y + z)(x + u + y − z).
7.9. Обозначим
![]()
Возведем в куб. Получим
![]()
Произведение корней преобразуем так:
![]()
выражение в скобках равно z. Придем к уравнению
z³ − 5z − 12 = 0.
Так как z = 3 — корень этого уравнения, в чем убеждаемся проверкой, то преобразуем уравнение к виду
z³ − 9z + 4z − 12 = 0, или (z − 3)(z² + 3z + 4) = 0.
Уравнение z² + 3z + 4 = 0 не имеет действительных корней. Следовательно, z = 3, что и требовалось доказать.
7.10. По условию а + b = −с. Возведем в куб
а³ + b³ + 3аb(а + b) = −с³
и заменим а + b на −с. Получим
а³ + b³ + с³ = 3аbс.
Возведем а + b + с = 0 в квадрат
а² + b² + с² = −2(ab + ас + bc)
и еще раз возведем в квадрат
а4 + b4 + с4 + 2(а²b² + а²с² + b²с²) = 4[а²b² + а²с² + b²с² + 2(а²bc + b²ас + с²ab)].
Поскольку а²bc + b²ас + с²ab = аbс(а + b + с) = 0, то
а4 + b4 + с4 = 2(а²b² + а²с² + b²с²).
Преобразуем левую часть тождества, которое нужно доказать:
а5(b² + с²) + b5(а² + с²) + с5(а² + b²) = а²b²(а³ + b³) + а²с²(а³ + с³) + b³с²(b³ + с³).
Заменим а³ + b³ на 3аbс − с³ и поступим аналогично с остальными скобками:
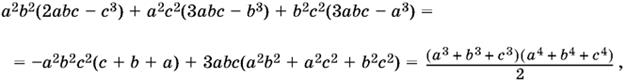
что и требовалось доказать.
7.11. Если данное равенство доказано при x ≥ 0 и любом y, то оно верно для всех x и y. Действительно, пусть x < 0. Тогда левую часть можно записать в виде
|−(x + y)| + |−(x − y)| = |(−x) − y)| + |(−x) + y|,
а правую — в виде
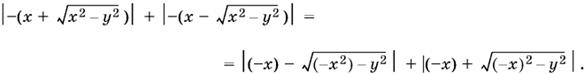
Поскольку −x > 0, то равенство стоящих справа выражений будет доказано.
Итак, пусть x ≥ 0. Рассмотрим два случая: |y| ≤ x и |y| > x.
1. x ≥ 0, |y| ≤ x, т. е. −x ≤ y ≤ x. Тогда x² − y² ≥ 0 и
![]()
— неотрицательное действительное число. Кроме того
![]()
и равенство примет вид
![]()
2. x ≥ 0, |y| > x, т. е. y < −x или y > x. Левая часть равенства в этом случае равна 2|y| (случаи y < −x и y > x разберите самостоятельно). Так как |y| > x, то
![]()
следовательно,
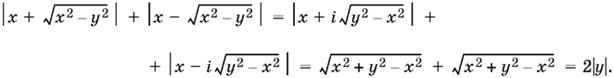
Тем самым доказательство тождества закончено.
7.12. Так как обе части равенства неотрицательны, то можно каждую из них возвести в квадрат
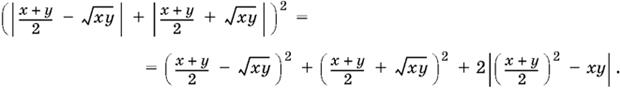
Осуществим действия, указанные в скобках, и заметим, что (x + y/2)² ≥ xy. Получим
x² + 2ху + y².
Если возвести в квадрат правую часть, то получим
x² + 2|ху| + y².
Так как по условию ху = |ху|, то равенство доказано.
7.13. Возведем выражение
a⅓ + b⅓ = −c⅓ (1)
в куб. Получим
a + b + 3a⅓b⅓(a⅓ + b⅓) = −c. (2)
Подставим (1) в (2):
a + b − 3a⅓b⅓c⅓ = −c.
т. е.
a + b + c = 3a⅓b⅓c⅓,
или
(а + b + с)³ = 27аbс.
7.14. По условию
24х² + 48х + 26 = (ax + b)³ − (cx + d)³,
т. е. коэффициенты многочленов слева и справа равны. Прежде чем преобразовать правую часть, заметим, что коэффициент при x³ равен нулю, т. е. а³ − с³ = 0, или а = с. Тогда получим, что
(ax + b)³ − (ax + d)³ = 3а²(b − d)x² + 3а(b² − d²)x + b³ − d³.
Следовательно,
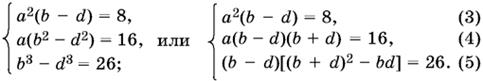
Из (3): b − d = 8/a². Из (4) с учетом (3): b + d = 2а.
Далее найдем:
![]()
Подставим выражения для b − d , b + d и bd в (5):
![]()
(так как а > 0).
Соответственно, b = 3, d = 1.
Ответ. 2x + 3; 2x + 1.