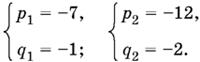Сборник задач по математике с решениями - А. А. Рывкин, Е. Б. Ваховский 2003
Решения
Делимость многочленов. Теорема Безу. Целые уравнения
8.1. Положив x − 5 = y, приведем уравнение к виду
(y + ½)4 + (y − ½)4 = 1, или (2у + 1)4 + (2у − 1)4 = 16,
откуда после простых преобразований получим
16y4 + 24y2 − 7 = 0.
Ответ. x1,2 = 5 ± i√7/2; x3 = 4,5; x4 = 5,5.
8.2. Перемножим попарно первую и третью скобки и две оставшиеся:
(12х² + 11х + 2)(12х² + 11х − 1) = 4.
Обозначив 12х² + 11х + ½ = y, получим
(y + 3/2)(y − 3/2) = 4,
откуда
y1 = −5/2, у2 = 5/2.
Остается решить два квадратных уравнения.
Ответ.
![]()
8.3. Запишем уравнение в виде
x² − 17 = 3y²
и рассмотрим случаи x = 3k, x = 3k ± 1. B первом случае левая часть примет вид 9k² − 17 и не будет делиться на три. B остальных двух случаях в левой части получим
9k² ± 6k − 16,
что снова не делится на три. Поскольку правая часть всегда делится на три, то уравнение не имеет целых решений.
8.4. Решим уравнение относительно x:
![]()
Так как уравнение имеет действительные корни лишь при
25 − y² ≥ 0, т. е. |y| ≤ 5,
то остается перебрать все целые значения y, для которых
![]()
— целое число: y = 0, y = ±3, y = ±4, y = ±5. Для каждого значения y найдем два значения x.
Ответ. (10, 0), (−10, 0); (−1, −3), (−17, −3); (1, 3), (17, 3); (−6, −4), (−18, −4); (6, 4), (18, 4); (−15, −5), (15, 5).
8.5. По определению деления имеем тождество
x99 + x³ + 10х + 5 = Q(x) (x² + 1) + ax + b,
которое справедливо всюду в области комплексных чисел. Так как частное Q(x) нам неизвестно и оно нас не интересует, то в качестве значения x нужно выбрать один из корней выражения x² + 1, например x = i. Подставив x = i, получим
i99 + i³ + 10i + 5 = аi + b, т. е. 8i + 5 = аi + b,
откуда а = 8, b = 5.
Ответ. 8х + 5.
8.6. Перепишем уравнение в виде
y² 2x² + 1/x² + 2 = 6.
Если x² ≥ 1, то 2x² + 1/x² + 2 ≥ 1.
Так как x = 0 не является целочисленным решением уравнения, то можно утверждать, что y² ≤ 6. Остается рассмотреть случаи: y² = 0, y² = 1, y² = 4. Первый и второй не приводят к действительным значениям x. Для y² = 4 находим x² = 4.
Ответ. (2, 2), (2, −2); (−2, 2), (−2, −2).
8.7. Подставим в данное уравнение x = √3 + 1. После простых вычислений и преобразований получим
36 + 10а + 4b + (22 + 6а + 2b)√3 = 0.
Сумма двух чисел, из которых одно рациональное, а другое иррациональное, может равняться нулю, только если оба числа равны нулю:
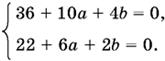
(1).
Решая эту систему, найдем а = −4, b = 1. Поскольку уравнение
x4 − 4x³ + x² + 6x + 2 = 0
одним из своих корней имеет число √3 + 1, а все коэффициенты уравнения — целые, то следует ожидать, что наряду с этим корнем должен существовать и корень √3 − 1. Подставим это значение x в уравнение и соберем отдельно рациональные и иррациональные члены. Получим
36 + 10а + 4b − (22 + 6а + 2b)√3 = 0,
что приводит к той же системе уравнений (1) и имеет место при а = −4, b = 1. Следовательно, x = 1 − √3 — второй корень данного в условии уравнения.
Разделив многочлен x4 − 4x³ + x² + 6x + 2 на
(x − √3 − 1)(x + √3 − 1) = x² − 2x − 2,
получим квадратный трехчлен x² − 2x − 1, корнями которого являются числа 1 + √2.
Ответ. x1,2 = 1 ± √3; x3,4 = 1 ± √2.
8.8. Из теоремы Виета получаем неравенства:
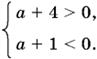
Добавляем к ним условие неотрицательности дискриминанта:
(а + 1)² − 4(а + 4) ≥ 0.
Приходим к системе неравенств
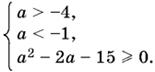
Последнему неравенству удовлетворяют числа а, лежащие вне промежутка между корнями: а ≤ −3, а ≥ 5.
Ответ. −4 < а ≤ −3.
8.9. Пусть х1, х1q и х1q² — корни данного уравнения. По теореме Виета имеем систему
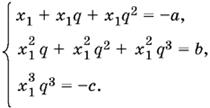
Из этих уравнений нужно исключить x1 и q. Поскольку из первого уравнения следует х1(1 + q + q³) = −а, то второе примет вид
b = х1²q(1 + q + q²) = x1q(−а),
т. е. x1q = − b/a, откуда
−b³/a³ = −c.
Ответ. са³= b³.
8.10. По теореме Виета
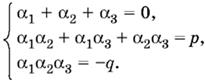
Возведем первое уравнение в квадрат:
α1² + α2² + α3² + 2(α1α2 + α1α3 + α2α3) = 0,
откуда найдем α1² + α2² + α3² . Как видим, последнее уравнение не понадобилось.
Ответ. α1² + α2² + α3² = −2p.
8.11. Разделив x³ + ax + 1 на x − α, получим в частном x² + αx + а + α², а в остатке α³ + aα + 1. Условия задачи будут выполняться тогда и только тогда, если
α³ + aα + 1 = 0,
x² + αx + а + α² > 0 при всех x.
Чтобы выполнялось второе условие, дискриминант −3α² − 4а должен быть отрицательным, т. е. 3α² + 4а > 0.
Число а не может быть равно нулю, так как уравнение а³ + аα + 1 = 0 не удовлетворяется при а = 0. Из первого уравнения a = −1 + α³/α. Поэтому должно быть
3α² − 41 + α³/α > 0.
Если α > 0, то последнее неравенство эквивалентно такому:
3α³ − 4(α³ + 1) > 0,
или −α³ > 4, y которого нет решений.
Если α < 0, то получим
3α³ − 4(α³ + 1) < 0,
или
![]()
Ответ.
![]()
8.12. Пусть
P(x) = (x − 2)(x − 3) Q(x) + ax + b,
где ax + b — остаток, который надо найти.
По теореме Безу P(2) = 5, а P(3) = 7. Подставим x = 2 и x = 3 в правую часть написанного выше тождества. Получим систему относительно а и b
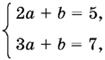
откуда а = 2, b = 1.
Ответ. 2x + 1.
8.13. Многочлен x4 + 1 делится на x² + рх + q тогда и только тогда, когда
x4 + 1 = (x² + ax + b)(x² + рх + q).
Раскрывая в правой части скобки и приравнивая коэффициенты при одинаковых степенях x, получим систему уравнений
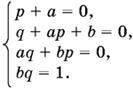
Из первого и последнего уравнений находим а = −p, b = 1/q. Подставляя в оставшиеся два уравнения, получим
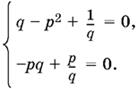
Второе уравнение можно переписать так: p(q − 1/q) = 0.
Если p = 0, то первое уравнение не имеет действительных решений. Остается q = 1/q, т. е. q = ±1. Подставляя найденные значения q в первое уравнение, увидим, что, когда q = 1, р² = 2 и p = ±√2, а когда q = −1, р² = −2 и действительных решений нет. Итак, получаем две возможности: либо p = √2 и q = 1, либо p = −√2 и q = 1.
Чтобы закончить решение, нужно сделать проверку. Можно было бы разделить x4 + 1 поочередно на каждый из двух трехчленов: x² + √2 x + 1 и x² − √2 x + 1. Однако проще убедиться, что
x4 + 1 = (x² + √2 x + 1)(x² − √2 x + 1).
Ответ. р1 = − √2, q1 = 1; р2 = √2, q2 = 1.
8.14. После замены x − 1 = y получим многочлен
(y + 1)2n + 1 − (2п + 1)(y + 1)n + 1 + (2п + 1)(y + 1)n − 1,
который должен делиться на y³. Вычислим его коэффициенты при y0, y1 и y2.
Свободный член этого многочлена равен
1 − (2n + 1) + (2n + 1) − 1 = 0;
коэффициент при y
2n + 1 − (2n + 1)(n + 1) + (2n + 1)n = 0;
коэффициент при y²
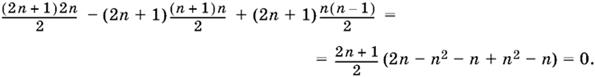
Тем самым утверждение доказано.
8.15. Чтобы данный многочлен делился на x² − x + q без остатка, должно выполняться тождество
6х4 − 7x³ + рх² + 3x + 2 = (x² − x + q)(6х² + ax + b).
B правой части стоит многочлен
6x4 + (а − 6)x³ + (b − а + 6q)x² + (−b + qа)x + qb.
Так как многочлены равны тождественно, получаем систему
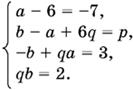
Из первого уравнения а = −1. Из третьего и четвертого уравнений исключаем b. Приходим к уравнению
q² + 3q + 2 = 0,
откуда
q1 = −1, q2 = −2.
Сложив второе и третье уравнения, также исключим b:
5q − 2 = p.
Следовательно,
р1 = −7, p2 = −12.
Итак, возможны два решения.
Ответ.