Возрастание, убывание, экстремум функции (без нахождения производной) - Функции - Алгебра и начала анализа - Базовый уровень

164. Функция у = f(x) определена на промежутке (—4; 6). На рисунке 173 изображён график её производной. Укажите число точек максимума функции у = f(x) — х — 2 на промежутке (—4; 6).

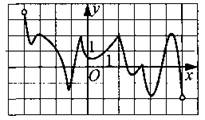
Рис. 173.

165. Функция у = f(x) определена на промежутке (—7; 3). На рисунке 174 изображён график её производной. Укажите точку минимума функции у = f(x) на промежутке (—7; 3).

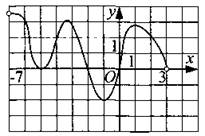
Рис. 174.

166. Функция у = g(х) определена на промежутке (—6; 4). На рисунке 175 изображён график её производной. Найдите точку х₀, в которой функция у = g(х) принимает наибольшее значение на отрезке [—4; 1].

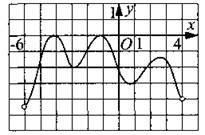
Рис. 175.

167. Функция у = f(x) определена на промежутке (—4; 7). На рисунке 176 изображён график её производной. Найдите точку x₀, в которой функция у = f(x) принимает наименьшее значение на отрезке [—2; 5].

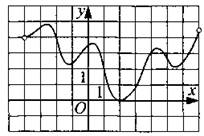
Рис. 176.

168. Функция у = f(x) определена и дифференцируема на интервале (—6; 4). На рисунке 177 изображён график её производной. В какой точке функция у = f(x) достигает своего наименьшего значения?

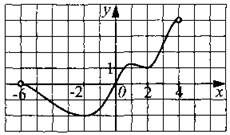
Рис. 177.

169. Функция у = f(x) определена на интервале (—3; 5). На рисунке 178 изображён график её производной. Укажите количество точек максимума функции у = f(x).

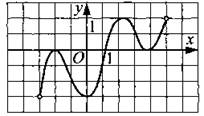
Рис. 178.

170. Функция у = f(x) определена на интервале (—3; 5). На рис. 179 изображён график её производной. Укажите количество точек минимума.

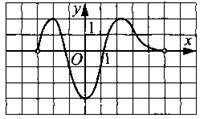
Рис. 179.

171. Функция у = f(x) определена на промежутке (—3; 5). На рисунке 180 изображён график её производной. Укажите количество точек экстремума.

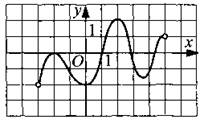
Рис. 180.