Призма. Параллелепипед - Стереометрия - Геометрия - Базовый уровень

832. В сосуд, имеющий форму правильной треугольной призмы, налили воду (см. рис. 353). Уровень воды достигает 20 см. На какой высоте (в сантиметрах) будет находиться уровень воды, если её перелить в другой такой же сосуд, у которого сторона основания в 2 раза больше, чем у первого?

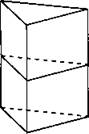
Рис. 353.

833. Объём правильной шестиугольной призмы равен 3√3, сторона основания равна 2 (см. рис. 354). Найдите высоту призмы.

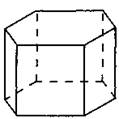
Рис. 354.

834. Найдите площадь боковой поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 10 и 24, а её боковое ребро равно 20 (см. рис. 355).

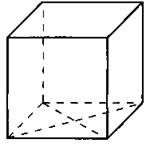
Рис. 355.

835. Найдите площадь поверхности правильной четырёхугольной призмы, если сторона её основания равна 10, а высота равна 6 (см. рис. 356).

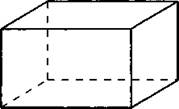
Рис. 356.

836. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру (см. рис. 357). Найдите площадь боковой поверхности исходной призмы, если площадь боковой поверхности отсечённой треугольной призмы равна 18.

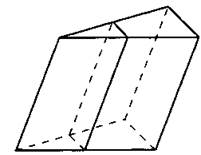
Рис. 357.

837. Найдите квадрат расстояния между вершинами D и С₁ прямоугольного параллелепипеда ABCDAiBiCiDi со сторонами АВ = 6, AD = 7, АА₁ = 9.

838. В сосуд, имеющий форму правильной тринадцатиугольной призмы налили 720 см³ воды, а затем полностью погрузили туда деталь. При этом уровень жидкости в сосуде поднялся с отметки 18 см до отметки 21 см. Чему равен объём детали? Объём выразите в см³.

839. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра равны 9,3. Найдите расстояние между точками С₁ и Е₁.

840. Найдите объём многогранника, вершинами которого являются точки С, A₁, B₁, C₁, D₁ параллелепипеда ABCDA₁B₁C₁D₁, у которого АВ = 8, AD = 12, АА₁ = 4 (см. рис. 358).

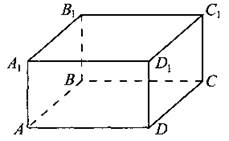
Рис. 358.

841. Найдите объём призмы, в основаниях которой лежит квадрат со стороной 2,5, а боковые рёбра равны 8√3 и наклонены к плоскости основания под углом 60°.

842. Дан прямоугольный параллелепипед ABCDA₁B₁C₁D₁, для которого AA₁ = 17, АВ = 19, AD = 17√3. Найдите угол BiCB. Ответ дайте в градусах.

843. Найдите котангенс угла ABD₂ многогранника, изображённого на рисунке 359.

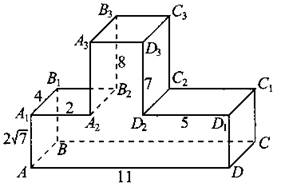
Рис. 359.

844. Дана правильная шестиугольная призма ABCDEFA₁B₁C₁D₁E₁F₁, площадь основания которой равна 17, а боковое ребро 8. Найдите объём многогранника, вершинами которого являются точки С, D, Е, F, C₁, D₁, E₁, F₁.

845. Найдите косинус угла ВА₂А₃ многогранника, изображённого на рисунке 360. Все двугранные углы многогранника — прямые.

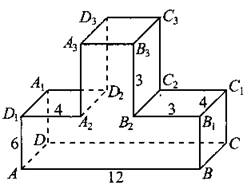
Рис. 360.

846. Найдите объём многогранника, вершинами которого являются точки C, D, A₁, В₁, C₁, D₁ прямоугольного параллелепипеда ABCDA₁B₁C₁D₁ (см. рис. 361), у которого АВ = 4, AD = 22, АА₁ = 6.

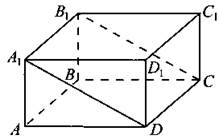
Рис. 361.

847. Найдите угол АВ2В многогранника, изображённого на рисунке 362. Ответ дайте в градусах.

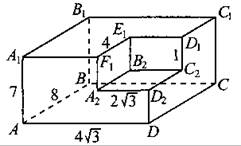
Рис. 362.

848. Прямоугольный параллелепипед описан около сферы радиуса 23,5. Найдите его объём.

849. Найдите расстояние между вершинами А₁ и Е многогранника, изображённого на рисунке 363. Все двугранные углы многогранника — прямые.

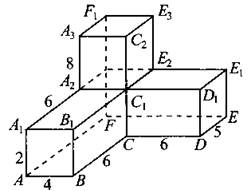
Рис. 363.

850. Найдите квадрат расстояния между вершинами А и В₂ многогранника, изображённого на рисунке 364.

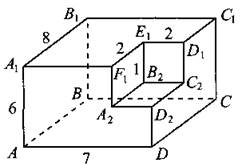
Рис. 364.

851. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ сторона основания равна 2, а высота — 19. Найдите квадрат расстояния между А и E₁.

852. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 48 и 14. Площадь её поверхности равна 728. Найдите высоту призмы.

853. В правильной шестиугольной призме ABCDEFA₁B₁C₁D₁E₁F₁ все рёбра основания и боковые рёбра равны 8. Найдите угол АС₁С. Ответ дайте в градусах.

854. В правильной четырёхугольной призме ABCDA₁B₁C₁D₁ с основаниями ABCD и A₁B₁C₁D₁ сторона основания АВ равна 4, а высота AA₁ равна 8√2. Найдите расстояние между точкой С и серединой бокового ребра АА₁.

855. Найдите расстояние между вершинами D и В₁ прямоугольного параллелепипеда, для которого АВ = АА₁ = 17,5, AD = 17,5√2.