Комбинации тел - Стереометрия - Геометрия - Базовый уровень

869. Основания цилиндра и конуса совпадают, а площадь полной поверхности цилиндра в два раза больше площади полной поверхности конуса. Найдите длину образующей конуса, если высота цилиндра равна 10.

870. Объём конуса равен объёму цилиндра, а высота конуса в два раза больше высоты цилиндра. Площадь основания цилиндра равна 15. Найдите площадь основания конуса.

871. Сфера вписана в прямой круговой цилиндр с площадью основания 24. Чему равна площадь сферы?

872. В шар вписан цилиндр с площадью основания 4π и синусом угла между образующей цилиндра и диагональю его осевого сечения, равным 1/5. Найдите отношение площади поверхности шара к площади основания цилиндра.

873. В правильном тетраэдре, площадь поверхности которого равна 18 см², отметили середины всех его рёбер и построили октаэдр с вершинами в этих серединах. Найдите площадь поверхности построенного октаэдра.

874. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны Найдите объём параллелепипеда.

875. Прямоугольный параллелепипед описан около цилиндра. Радиус основания цилиндра равен 3. Объём параллелепипеда равен 72 (см. рис. 373). Найдите высоту цилиндра.

Рис. 373.

876. Прямоугольный параллелепипед описан около цилиндра (см. рис. 374), радиус основания которого равен 5. Высота цилиндра равна 7. Найдите объём параллелепипеда.

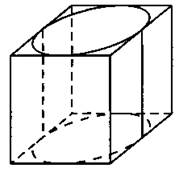
Рис. 374.

877. Основанием прямой призмы является прямоугольный треугольник с катетами 5 и 12. Боковые рёбра равны 4/π (см. рис. 375). Найдите объём цилиндра, описанного около этой призмы.

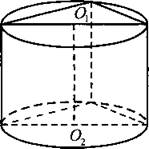
Рис. 375.

878. Прямоугольный параллелепипед описан около сферы радиусом 2,5 (см. рис. 376). Найдите его объём.

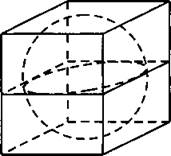
Рис. 376.

879. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 377). Вычислите объём цилиндра, если объём конуса равен 15.

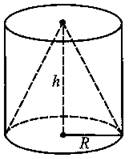
Рис. 377.

880. В окружность основания цилиндра вписан правильный треугольник (см. рис. 378). Найдите объём пирамиды той же высоты, что и цилиндр, в основании которого лежит этот треугольник, если объём цилиндра равен π√3.

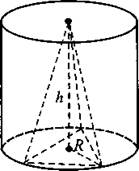
Рис. 378.

881. В основании пирамиды лежит правильный треугольник (см. рис. 379). В него вписана окружность, являющаяся основанием цилиндра той же высоты, что и пирамида. Найдите объём цилиндра, если объём пирамиды равен √3/π.

Рис. 379.

882. В основании пирамиды лежит правильный треугольник (см. рис. 379). В него вписана окружность, являющаяся основанием цилиндра, той же высоты, что и пирамида. Найдите объём пирамиды, если объём цилиндра равен π√3.

883. Цилиндр и конус имеют общее основание и общую высоту (см. рис. 380). Вычислите объём конуса, если объём цилиндра равен 12.

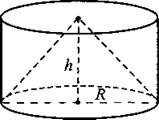
Рис. 380.

884. Правильная четырёхугольная призма описана около цилиндра, высота которого равна 2 (см. рис. 381). Найдите радиус цилиндра, если известно, что площадь боковой поверхности призмы равна 12.

885. Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 1. Найдите объём параллелепипеда (см. рис. 381).

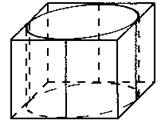
Рис. 381.

886. Объём цилиндра равен 9. У конуса радиус основания в 3 раза больше, а высота в 2 раза меньше. Найдите объём конуса.