Математика сборник задач для подготовки к ЕГЭ
Многочлены и их корни - Краткий теоретический справочник - МАТЕМАТИКА ПОДГОТОВКА К ЕГЭ
Определение многочлена
Многочленом степени n(n ∈ N0) называется всякое выражение вида
где 
Всякое вещественное число, отличное от нуля, принято трактовать как многочлен нулевой степени. Числа an, an-1 ,..., а1, а0 называются коэффициентами многочлена, аn — старший коэффициент, а0 — свободный член.
Число х0 называется корнем многочлена f(x), если f(x0) = 0.
Квадратный трёхчлен
Квадратный трёхчлен — это многочлен степени 2:
Если х1, x2 — корни f(x), то 
(Теорема Виета).
Если второй коэффициент делится на 2, то есть f(x) = aх2 + 2kх + c, то 
Если старший коэффициент равен 1, то есть f(x) = х2 + рх + q, то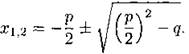 
Выражение b2 — 4ас называется дискриминантом соответствующего многочлена f(x) (уравнения f(x) = 0). Дискриминант принято обозначать большой буквой D. Отметим, что 
*Теорема Безу и схема Горнера
Для любого многочлена степени n > 0
и любого числа х0 ∈ R найдётся такой многочлен степени n — 1
что справедливо равенство
(Теорема Безу),
причём коэффициенты q(x) могут быть вычислены по следующему алгоритму:
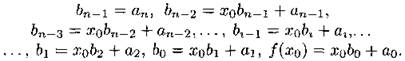
Результаты вычисления коэффициентов многочлена q(x) удобно помещать в таблицу (схему Горнера).
|
|
an |
an-1 |
an-2 |
... |
ai+1 |
аi |
... |
a2 |
а1 |
a0 |
|
X0 |
bn-1 |
bn-2 |
bn-3 |
... |
bi |
bi-1 |
... |
b1 |
b0 |
f(x0) |
Понятно, что если х0 — корень многочлена f(x), то f(х0) = 0 и, следовательно,
f(х) = (х — x0) q(x) (следствие из теоремы Безу).
Таким образом, чтобы выяснить, является ли число х0 корнем многочлена f(x), нужно заполнить приведённую выше таблицу (схему Горнера). Если f(x0) окажется равным 0, то х0 — корень. В противном случае х0 — не корень f(х).
Приведём еще одну теорему о многочленах и следствие из неё, касающееся рациональных корней многочлена.
Теорема. Пусть 
— многочлен с целыми коэффициентами. Если несократимая дробь (рациональное число) p/q является корнем многочлена f(х), то
Следствие. Пусть 
— многочлен с целыми коэффициентами. Тогда все рациональные корни многочлена f(x) являются целыми и являются делителями свободного члена a0.
Эти теоремы будут очень полезными при выполнении некоторых заданий части В и части С, их использование существенно экономит время решения.
Пример 1. Найдите целые корни уравнения х4 + 3х3 + х2 — 3х — 2 = 0.
Решение. По следствию целые корни находятся среди делителей свободного члена: ±1; ±2. Проверяем по схеме Горнера каждое из этих чисел.
|
|
1 |
3 |
1 |
-3 |
-2 |
|
|
1 |
1 |
4 |
5 |
2 |
0 |
корень |
|
1 |
1 |
5 |
10 |
12 |
|
не корень (не кратный корень) |
|
-1 |
1 |
3 |
2 |
0 |
|
корень |
|
-1 |
1 |
2 |
0 |
|
|
корень (кратности 2) |
Данное уравнение имеет 3 корня: 1; —1; —2, причём —1 — корень кратности 2.
Пример 2. Решите уравнение 6х4 + 17x3 + 20х2 + 14х + 3 = 0.
Решение. По теореме все рациональные корни уравнения находятся среди чисел p/q, где 
Делители 3: ±1; ±3.
Делители 6: ±1; ±2; ±3; ±6.
Числа вида 
Видим, что корнями могут быть лишь отрицательные числа. Поэтому проверяем числа 
|
|
6 |
17 |
20 |
14 |
3 |
|
|
-1 |
6 |
11 |
9 |
5 |
-2 |
не корень |
|
-1/2 |
6 |
14 |
13 |
15/2 |
-3/4 |
не корень |
|
-1/3 |
6 |
15 |
15 |
9 |
0 |
корень |
Данное уравнение эквивалентно 
Делители 3: ±1; ±3.
Делители 2: ±1; ±2.
Числа вида 
Корнями могут быть лишь отрицательные числа, причём —1 и —1/2 не являются корнями (проверили выше).
Проверяем числа —3; —3/2.
|
|
2 |
5 |
5 |
3 |
|
|
-3 |
2 |
-1 |
8 |
-21 |
не корень |
|
-3/2 |
2 |
2 |
2 |
0 |
корень |
Данное уравнение эквивалентно 
x2 + x + 1 = 0 — корней нет.
Ответ: -1/3, -3/2.