Математика сборник задач для подготовки к ЕГЭ
Комбинированные уравнения - Уравнения. Системы уравнений - Алгебра и начала анализа - Повышенный уровень 1
Решите уравнение (979—980):
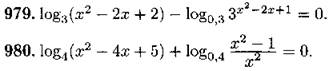
Решите систему уравнений (981—989):
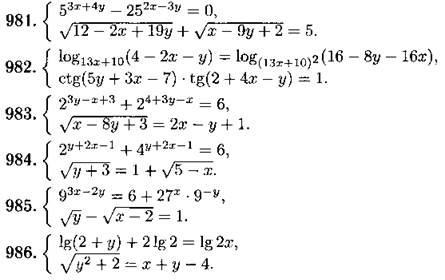
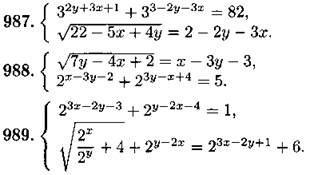
Решите уравнение (990—994):
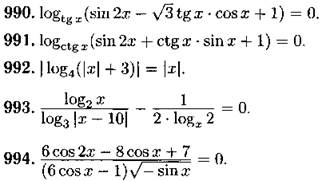
Решите систему уравнений (995—996):
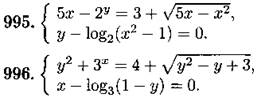
Решите уравнение (997—998):
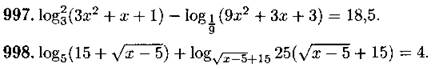
Решите систему уравнений (999—1018):
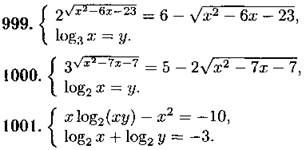
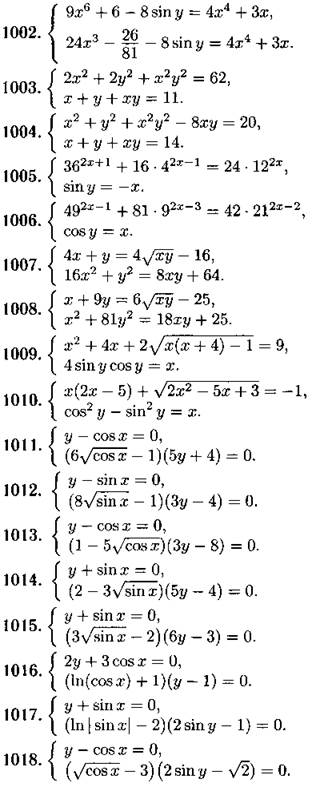
Решите уравнение (1019—1020):
![]()
Решите систему уравнений (1021—1022):
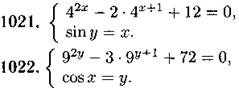
Решите уравнение (1023— 1024):
![]()
Решите систему уравнений (1025—1038):
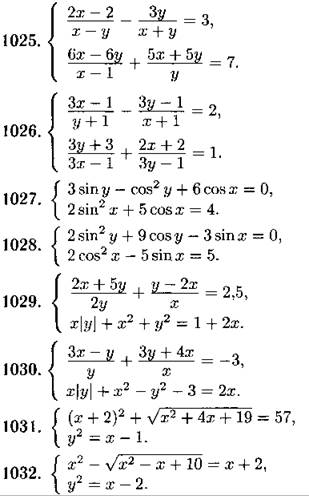
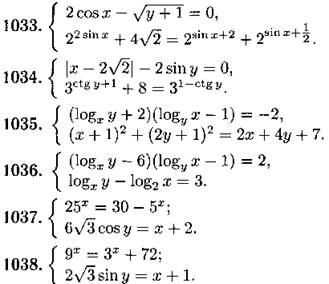
Решите уравнение (1039—1042):
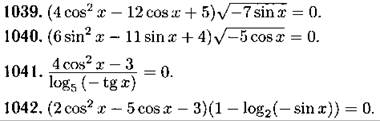
Решите систему уравнений (1043— 1044):
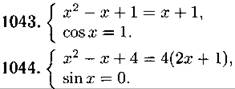
Решите уравнение (1045—1055):
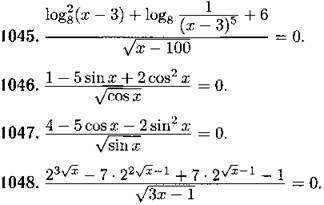
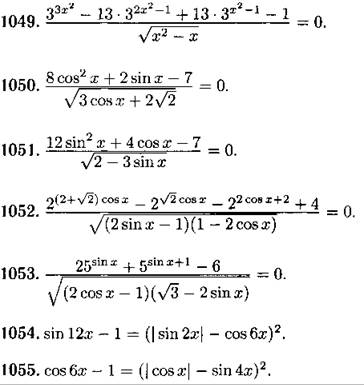
Решите систему уравнений (1056—1057):
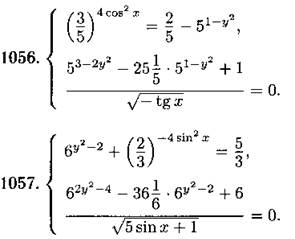
1058. a) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку [-3π; -3π/2].
1059. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку [5π/2; 7π/2].
1060. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку [π/3; π).
1061. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку [2π; 5π/2).
1062. Решите уравнение ![]()
1063. а) Решите уравнение (5 sin2 х + 4 cos х — 4) ln (x — 7) = 0.
б) Найдите все корни этого уравнения, принадлежащие промежутку [3π/2; 3π].
1064. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие отрезку [5π/2; 7π/2].
1065. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие отрезку [4π; 5π].
1066. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку [-π; 2π/5].
1067. а) Решите уравнение ![]()
б) Найдите все корни этого уравнения, принадлежащие промежутку (-4π/3; 5π/12).