Поурочные разработки по геометрии 10 класс
Перпендикулярные прямые в пространстве. Параллельные прямые, перпендикулярные к плоскости - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМОЙ И ПЛОСКОСТИ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) ввести понятие перпендикулярных прямых в пространстве;
2) доказать лемму о перпендикулярности двух параллельных прямых к третьей прямой;
3) дать определение перпендикулярности прямой и плоскости;
4) доказать теоремы, в которых устанавливается связь между параллельностью прямых и их перпендикулярностью к плоскости.
Ход урока
I. Организационный момент
Сообщить тему урока и поставить цели.
II. Устная работа
1) Что такое перпендикулярные прямые на плоскости?
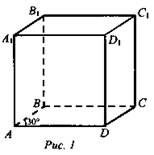
2) Дано: ABCDA1B1C1D1 - параллелепипед, ∠BAD = 30° (рис. 1).
Найдите углы между прямыми АВ и A1D1; А1В1 и AD; АВ и B1С1. (30°, 30°, 150°).
III. Изучение нового материала
1) Рассмотрим модель куба. Как называются прямые АВ и ВС? (перпендикулярные). Найдите угол между прямыми АА1 и DC; ВВ1 и AD. Эти прямые тоже перпендикулярные.
Вводится понятие перпендикулярности двух прямых в пространстве.
В пространстве перпендикулярные прямые могут пересекаться и могут быть скрещивающимися.
Рассмотрим прямые АА1, СС1 и DC (рис. 2).
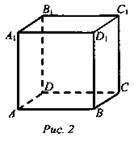
Прямая AA1 параллельна прямой СС1, а прямая СС1 перпендикулярна прямой CD. Нами установлено, что АА1 перпендикулярна CD.
- Сформулируйте это утверждение.
Лемма
Если одна из двух параллельных прямых перпендикулярна к третьей прямой, то и другая прямая перпендикулярна к этой прямой.
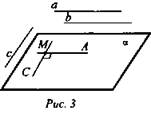
Дано: а || b, а ⊥ с (рис. 3).
Доказать: b ⊥ с.
Доказательство:
Через точку М пространства, не лежащую на данных прямых, проведем прямые МА и МС, параллельные соответственно прямым а и с. Так как а ⊥ с, то ∠AMC = 90° (рис. 3).
По условию b || а, а по построению а || МА, поэтому b || МА. Итак, прямые b и с параллельны соответственно прямым МА и МС, угол между ними равен 90°. Это означает, что угол между прямыми b и с также равен 90°, то есть b ⊥ с. Лемма доказана.
2) Рассмотрим модель куба (рис. 4).
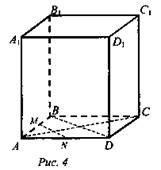
- Найдите угол между прямой АА1 и прямыми плоскости (ABC): АВ, AD, AC, BD, MN. (90°, 90°, 90°, 90°, 90°). Вывод: прямая АА1 перпендикулярна любой прямой, лежащей в плоскости (ABC). Такие прямые называются перпендикулярными.
Дается четкое определение прямой, перпендикулярной к плоскости. Вводится обозначение а ⊥ α (рис. 5).
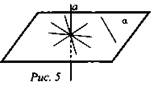
3) Доказать теорему:
Если одна из двух параллельных прямых перпендикулярна к плоскости, то и другая прямая перпендикулярна к этой плоскости.
Задача № 118
Дано: α, В, С, D, О ∈ α; А, М, О ∈ α, а ⊥ α (рис. 6).
Какие из углов ∠AOB, ∠MOC, ∠DAM, ∠DOA, ∠BMO прямые?
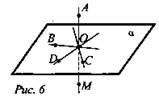
Решение: Так как точка О ∈ α и О ∈ α ⇒ а ∩ α = точка О; ∠AOB, ∠MOC, ∠DOA - прямые.
Дано: а || а1, а ⊥ α (рис. 7).
Доказать: а1 ⊥ х.
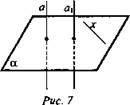
Доказательство:
x ⊂ α, x - произвольная прямая. Из условия а ⊥ α следует (по определению перпендикулярности прямой и плоскости), что а ⊥ х; так как a1 || а (по условию) и а ⊥ х, то (согласно лемме о перпендикулярности двух параллельных прямых к третьей прямой) а1 ⊥ х. Итак, прямая а перпендикулярна к произвольной прямой х, лежащей в плоскости α. А это означает, что а1 ⊥ α.
4) Доказать обратную теорему: если две прямые перпендикулярны к плоскости, то они параллельны. Доказательство: рассмотрим прямые а и b, перпендикулярные к плоскости α. Докажем, что они параллельны.
Рис. 47 (б) учебника на доске.
Через какую-нибудь точку М прямой b проведем прямую b1, параллельную прямой а. По предыдущей теореме b1 ⊥ α. Докажем, что прямая b1 совпадает с прямой b. Тем самым будет доказано, что а || b. Допустим, что прямые b и b1 не совпадают. Тогда в плоскости β, содержащей прямые b и b1, через точку М проходят две прямые, перпендикулярные к прямой с, по которой пересекаются плоскости α и β. Но это невозможно, следовательно, а || b. Теорема доказана.
IV. Закрепление изученного материала
Задача № 117
Дано: DABC - тетраэдр; М ∈ АВ : AM = BM, N ∈ АС: AN = NC; ВС ⊥ AD (рис. 8).
Доказать: AD ⊥ MN.
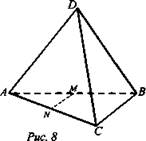
Доказательство:
1) MN - средняя линия ΔАВС ⇒ MN || ВС;
2) по лемме, так как ВС ⊥ AD, то MN ⊥ AD.
Задача № 120
Дано: ABCD - квадрат, АВ = а, АС ∩ BD = О, OK ⊥ (ABC), ОК = b (рис. 9).
Найти: АК, ВК, СК, DK.
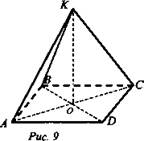
Решение:
1) АК = ВК = СК = DK следует из равенства. ΔАОК, ΔВОК, ΔСОК, ΔDOK равны по двум катетам (прямая ОК перпендикуляр на к плоскости квадрата. ABCD, ОК ⊥ АС и OK ⊥ BD);

Домашнее задание
1) п. 15-16, вопросы 1, 2 (стр. 54).
2) № 116, 118.
Задача № 116
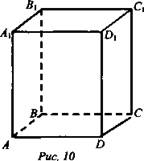
Дано: ABCDA1B1C1D1 - параллелепипед;
a) ∠BAD = 90°; б) АВ ⊥ DD1 (рис. 10).
Доказать:
![]()
Доказательство :
а) 1) ∠BAD = 90° ⇒ ABCD - прямоугольник; ![]()
![]()
2) ![]()
б) 1) ![]() (по лемме).
(по лемме).
2) ![]() (по лемме).
(по лемме).