Признак перпендикулярности двух плоскостей - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ

Цели урока:

1) ввести понятие угла между плоскостями;

2) дать определение перпендикулярных плоскостей;

3) доказать признак перпендикулярности двух плоскостей;

4) показать применение этого признака при решении задач.

Ход урока

I. Организационный момент

Сообщить тему урока, сформулировать цели урока.

II. Актуализация опорных знаний

Двое учеников у доски записывают решение домашнего задания: первый - № 167, второй - № 170.

Остальные отвечают на вопросы:

Точка А лежит на ребре двугранного угла.

1. Верно ли, что ∠ABC - линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру? (Нет.)

2. Верно ли, что ∠BAC - линейный угол двугранного угла, если лучи АВ и АС лежат в гранях двугранного угла? (Нет.)

3. Верно ли, что ∠BAC - линейный угол двугранного угла, если лучи АВ и АС перпендикулярны его ребру, а точки В а С лежат на гранях угла? (Да.)

4. Линейный угол двугранного угла равен 80°. Найдется ли в одной из граней угла прямая, перпендикулярная другой грани? (Нет.)

5. ∠ABC - линейный угол двугранного угла с ребром а. Перпендикулярна ли прямая а плоскости ABC? (Да.)

6. Верно ли, что все прямые, перпендикулярные данной плоскости и пересекающие данную прямую, лежат в одной плоскости? (Да.)

- Что называется углом между прямыми?

- Двугранным линейным углом двугранного угла?

- Углом между прямой и плоскостью?

III. Изучение нового материала

1. При пересечении двух плоскостей образуются четыре двугранных угла. Углом между пересекающимися плоскостями называется линейный угол φ этого двугранного угла, который 0° < φ ≤ 90° (рис. 1).

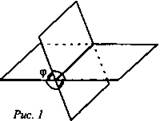
2. Если φ = 90°, то плоскости называются перпендикулярными (взаимно перпендикулярными) (рис. 2).

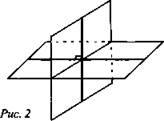
3. Приведите примеры взаимно перпендикулярных плоскостей (плоскости стены и пола, стены и потолка комнаты).

Ясно, что в этих случаях каждый из четырех двугранных углов, образованных пересекающимися плоскостями, прямой (рис. 2).

4. Рассмотрим признак перпендикулярности двух плоскостей.

Теорема

Если одна из двух плоскостей проходит через прямую, перпендикулярную к другой плоскости, то такие плоскости перпендикулярны.

Дано: α, β, АВ лежит в плоскости α, АВ ⊥ β, АВ ∩ α = А (рис. 3).

Доказать: α ⊥ β.

Доказательство: α ∩ β = АС, АВ ⊥ АС, так как АВ ⊥ β по условию. Проведем в плоскости β AD ⊥ AC. ∠BAD - линейный угол двугранного угла. Но ∠BAD = 90°, так как ВА ⊥ β. Значит, α ⊥ β.

IV. Формирование навыков и умений учащихся

1. При решении задач используются утверждения:

а) Плоскость, перпендикулярная к ребру двугранного угла, перпендикулярна к его граням (следствие).

б) Перпендикуляр, проведенный из любой точки одной из двух взаимно перпендикулярных плоскостей к линии их пересечения, есть перпендикуляр к другой плоскости (№ 178).

2. № 172. Дано: ΔАВС, ∠С = 90°, АС лежит в плоскости α, угол между плоскостями α и ABC равен 60°, АС = 5 см, АВ = 13 см (рис. 4).

Найти: расстояние от точки В до плоскости α.

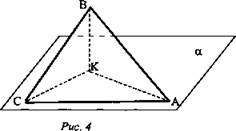
Решение: Построим ВК ⊥ α. Тогда КС - проекция ВС на эту плоскость. ВС ⊥ АС по условию, значит, по теореме о трех перпендикулярах, КС ⊥ АС. Отсюда следует, что ∠ВСК - линейный угол двугранного угла между плоскостью α и плоскостью треугольника ∠ВСК = 60°. Из ΔВСА по теореме Пифагора: Из ΔВКС: (Ответ: 6√3 см.)

3. Разобрать домашнее задание № 173, 174.

Наметить план решения № 173, 174.

V. Подведение итогов

Домашнее задани.

П. 23 № 173, № 174.

№ 173. Дано: ABCD - тетраэдр, CD ⊥ (ABC). AB = BC = AC = 6, BD = 3√7 (рис. 5).

Найти: двугранные углы DACB, DABC, BDCA.

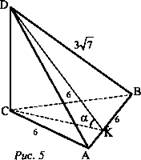
Решение:

1) Так как DC ⊥ (ABC), то (DCA) ⊥ (ABC) (признак перпендикулярности двух плоскостей) следовательно, двугранный угол DACB прямой.

2) Проведем СК ⊥ АВ, тогда АВ ⊥ DK по Теореме о трех перпендикулярах, следовательно, ∠DKC - линейный угол двугранного угла при ребре АВ тетраэдра. Из ΔАСК:

3) Из ΔBDK имеем:

4) Пусть ∠CKD = α, тогда Значит, двугранный угол DABC = 45°.

5) Так как ВС ⊥ DC и АС ⊥ DC, то ∠ABC - линейный угол двугранного угла BDCA. ∠ACB = 60° (ΔАВС - равносторонний), то двугранный угол BDCA равен 60°. (Ответ: 90°, 45°, 60°.)

№ 174. Дано: ABCD - тетраэдр,

Найти: двугранный угол ABCD.

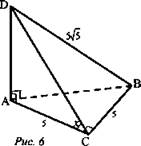
Решение:

1) Так как ∠DAB = ∠DAC = ∠ACB = 90° по условию, то DA ⊥ АВ, DA ⊥ AC. Значит, DA - перпендикуляр к плоскости ABC, АС - проекция наклонной DC на плоскость ABC.

2) По условию задачи ∠ACB прямой, то есть ВС ⊥ АС, следовательно, ВС ⊥ DC по теореме о трех перпендикулярах. Таким образом, ∠ACD - линейный угол двугранного угла ABCD.

3) Из ΔDCB: по теореме Пифагора

4) Из ΔDAC получаем: пусть ∠ACD = x, тогда (Ответ: 60°.)