Решение задач на применение аксиом стереометрии и их следствий - АКСИОМЫ СТЕРЕОМЕТРИИ И ИХ СЛЕДСТВИЯ

Цель урока:

- сформировать навык применения аксиом стереометрии и их следствий при решении задач.

Ход урока

I. Организационный момент

II. Актуализация знаний учащихся

1. Проверяется домашнее задание. Учитель отвечает на вопросы учащихся по домашней работе.

Двое учащихся готовят у доски доказательство следствий из аксиом.

Двое учащихся (I уровень) и двое учащихся (II уровень) работают по карточкам индивидуального опроса.

Карточка 1 (I уровень)

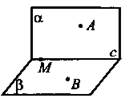
1. В пересекающихся плоскостях α и β взяты соответственно точки А и В, которые не лежат на линии их пересечения (прямой с). Точка М лежит на прямой с.

1) Построить линию пересечения плоскостей: а) α и МАВ; б) β и МАВ.

2) Найти общую точку плоскостей α, β и АMB.

2. Запишите символически н выполните рисунок: Прямая АВ пересекает плоскость α в точке О, a прямая CD лежит в плоскости α.

Карточка 1 (II уровень)

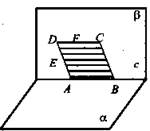
1. Через сторону АВ ромба ABCD проведена плоскость α. Точки Е, F - середина стороны AD и DC.

1) Постройте точку пересечения прямой EF с плоскостью α.

2) Вычислите расстояние от этой точки до точек А и В, если ВС = 12 см. (Ответ: 6 см и 18 см.)

2. Выполните рисунок: α ≠ β α ∩ β = а, М ∈ а, АВ ⊂ β.

Остальные учащиеся работают по готовому чертежу и отвечают на вопросы (фронтальная работа).

2. Устная работа.

а) Дан куб ABCDA1B1C1D1.

Найдите: 1) несколько точек, которые лежат в плоскости α; 2) несколько точек, которые не лежат в плоскости α; 3) несколько прямых, которые лежат в плоскости α; 4) несколько прямых, которые не лежат в плоскости α; 5) несколько прямых, которые пересекают прямую ВС; 6) несколько прямых, которые не пересекаются прямую ВС.

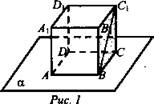
б) Заполните пропуски, чтобы получилось верное утверждение: 1) если А ∈ α, а ⊂ α, то А...α (пересекает); 2) если A ∈ α; В ∉ α, то АВ...α (принадлежит); 3) если А ∈ α; B ∈ α; С ∈ АВ, то С... α (принадлежит); 4) если М ∈ α; М ∈ β, α ⊂ β = а, то М...а (принадлежит).

Заслушиваются ответы учащихся у доски.

III. Решение задач

Задача № 7

Дано: a ∩ b = M, c ∩ a = A, c ∩ b = B, M ∉ с.

Доказать: 1. а ⊂ α; b ∩ α; с ⊂ α; 2. Лежат ли в одной плоскости все прямые, проходящие через точку M.

Решение: 1. Согласно второму следствию, пересекающиеся прямые а и b принадлежат плоскости α, следовательно, по аксиоме А2 прямая с лежит в плоскости α; (аксиома А2).

2. Все прямые, проходящие через точку М, не обязательно лежат в одной плоскости. Проиллюстрировать это утверждение на примере куба (см. рис. 1). АА1, АВ, AD проходят через точку А, но очевидно, не лежат в одной плоскости.

Задача № 1.

Решение: 1. Все прямые а, b, с лежат в одной плоскости. В этом случае, по следствию 2 можно провести плоскости, и через три прямые проходит одна плоскость (рис. 2).

.

2. Одна из трех прямых (с) не лежит в плоскости α, определяемой другими прямыми а и b. В этом случае через заданные три прямые проходят три различные плоскости, определяемые парами прямых а и b, а и с, b и с (см. рис. 3).

Задача № 10

Решение: а) Аналогично задаче № 7 - решить самостоятельно.

Взять выборочно тетради на проверку (рис. 4).

б) Нет (см. рис. 4). Если ABC ⊂ α; b ∩ α = В, b ⊄ α.

Задача

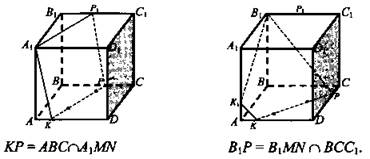
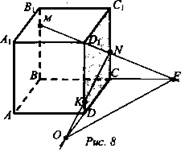
Дан куб ABCDA1B1C1D1 (рис. 5). Точка М лежит на ребре ВВ1, точка N лежит на ребре СС1 и точка К лежит на ребре DD1.

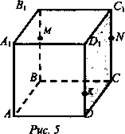
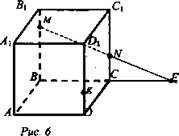
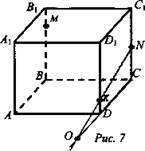
а) Назовите плоскости, в которых лежат точки М; точка N.

б) Найдите точку F - точку пересечения прямых MN и ВС. Каким свойством обладает точка F?

в) Найдите точку пересечения прямой KN и плоскости ABC.

г) Найдите линию пересечения плоскостей MNK и ABC.

Решение: При построении учащиеся проговаривают аксиомы, результат построения записывают с помощью символики. При решении данной задачи применяются аксиомы А2 и А3.

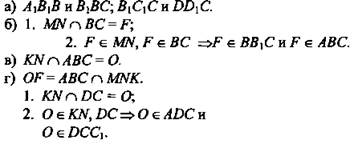
Дополнительная задача

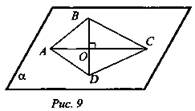
а) Докажите, что все вершины четырехугольника ABCD лежат в одной плоскости, если его диагонали АС и BD пересекаются (рис. 9).

б) Вычислите площадь четырехугольника, если AC ⊥ BD, АС = 10 см, CD = 12 см.

Решение:

а) Согласно второму следствию из аксиом, пересекающиеся прямые АС и BD определяют некоторую плоскость α. Прямая АС лежит в плоскости α, следовательно, все точки, в том числе А и С, принадлежат этой плоскости. Аналогично доказывается, что точки B и D принадлежат плоскости α (рис. 9).

б) Воспользуемся формулой где d1 и d2 - диагонали четырехугольника, а α - угол между ними.

IV. Подведение итогов

Оценки за урок.

Домашнее задание

1. П. 1-3.

2. Решение задач:

1 уровень - № 9, 13.

Дана треугольная призма АВСА1В1С1. М ∈ АВ. Построить точку пересечения прямой А1М с плоскостью ВВ1С1.

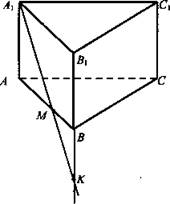
II уровень - № 11, 15.

Начертите изображение куба ABCDA1B1C1D1, выберете точки М и N грани ABCD. Построение линии пересечения плоскостей ABC и A1MN; B1MN и ВСС1.

Задача № 9

Дано: ABCD - параллелограмм (рис. 10). AC ∩ BD = т. О, О ∈ а, А ∈ а, В ∈ а..

Доказать: D ∈ α, С ∈ α.

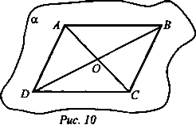
Решение: Так как А и В принадлежат α, то по аксиоме А2, прямая АВ и О принадлежит плоскости α, то АО ⊂ α, С ∈ АО, значит точка С ∈ α. Аналогично для точки D.

Задача № 11

Дано: a) A ∈ a, b ∩ а = О, А ∈ b (рис. 11).

Доказать: b ⊂ α.

Доказательство:

1. По первому следствию из аксиомы получаем, что прямая а и точка А определяют плоскости α.

2. Возьмем любую прямую (b), которая пересекается с прямой (а) и проходит через точку А. Тогда a ∩ b = O и O ∈ α, значит, О ∈ а. По аксиоме А2: b ⊂ α.

3. Аналогично все прямые, проходящие через точку А и пересекающие прямую а, лежат в плоскости α.

а) Нет, так как если две плоскости имеют одну общую точку, то они имеют общую прямую (по аксиоме А3).

б) Нет. Аналогично (а).

в) Да, это любые две пересекающиеся плоскости.

Задача № 15 (см. решение задачи 7)

I уровень

К = А1М ∩ ВВ1С.

II уровень