Поурочные разработки по геометрии 10 класс
Перпендикулярность прямых и плоскостей (повторение) - ДВУГРАННЫЙ УГОЛ. ПЕРПЕНДИКУЛЯРНОСТЬ ПЛОСКОСТЕЙ - ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
Цели урока:
1) повторить некоторые вопросы теории путем опроса учащихся;
2) решить задачи на применение этих вопросов.
Ход урока
I. Актуализация опорных знаний Фронтальный опрос
Трое учащихся на доске записывают решение домашних задач.
1. № 192. Дано: ABCDA1B1C1D1 - куб; B1D - диагональ куба; ∠BDB1 = α (рис. 1).
Найти: tg α.
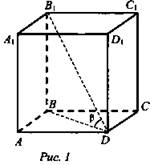
Решение:
1. Известно, что все ребра куба равны. Пусть АВ = AD = AA1 = а.
2. ΔABD - прямоугольный. BD2 = АВ2 + AD2 (теорема Пифагора); BD2 = а2 + а2 = 2а2; BD = a√2.
3. BD - проекция B1D на ABCD ⇒ угол между этими прямыми есть α.
4. В ΔB1BD: ![]() (Ответ: √2/2.)
(Ответ: √2/2.)
2. № 195. Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; BD, - диагональ параллелепипеда; АС1 = 12 см; ∠AD1B = 30°, ∠DD1B = 45° (рис. 2).
Найти: АВ, AD, DD1.
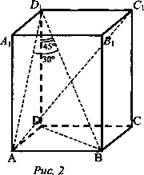
Решение:
1. Диагонали прямоугольного параллелепипеда равны; BD1 = АС1 = 12 см.
2. АВ ⊥ ADD1, поэтому AD1 - проекция диагонали на плоскость AA1D1D и ⇒ ∠AD1B = 30°.
3. Из ΔABD получаем: АВ = 6 см (по свойству катета, лежащего против угла в 30°.
4. Из ΔDD1В имеем: ![]()
![]()
5. Из ΔADB получаем: ![]()
![]() (Ответ: 6 см, 6 см, 6√2 см.)
(Ответ: 6 см, 6 см, 6√2 см.)
3. Задача по планиметрии
Дано: ΔABD, DM ⊥ АВ; АВ = 14, BD = 13, AD = 15 (рис. 3).
Найти: h.
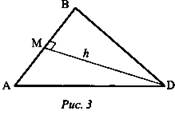
Решение:
1. Пусть MB - х, тогда АМ = АВ - х, то есть АМ = 14 - х.
2. Из ΔMBD и ΔAMD (прямоугольные так как MD ⊥ АВ); ![]()
![]() (в ΔMBD);
(в ΔMBD); ![]()
![]() (в ΔAMD). Приравняем правые части
(в ΔAMD). Приравняем правые части ![]()
![]()
3. Из ΔMBD, ![]() (Ответ: 12.)
(Ответ: 12.)
Два ученика работают по карточкам.
1. Три измерения прямоугольного параллелепипеда равны 1 м, 2 м, 3 м. Найдите: а) сумму длин всех его ребер; б) сумму площадей всех его граней; в) длины его диагоналей.
Дано: ABCDA1B1C1D1 - прямоугольный параллелепипед; АВ = 1 м, AD = 2 м, АА1 = 3 м (рис. 4).
Найти: а) сумму длин ребер; б) сумму площадей граней; в) длины диагоналей.
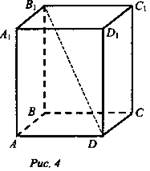
Решение:
а) В прямоугольном параллелепипеде 12 ребер; ![]()
![]() Это противоположные стороны прямоугольника.
Это противоположные стороны прямоугольника. ![]()
![]() Сумма ребер = 24 м.
Сумма ребер = 24 м.
б) 6 граней, причем противоположные равны; ![]()
![]()
в) Диагонали прямоугольного параллелепипеда равны; ![]()
![]() (Ответ: 24 м, 22 м2, √14 м.)
(Ответ: 24 м, 22 м2, √14 м.)
2. Три ребра параллелепипеда, имеющие общую вершину равны 2 м, 3 м и 5 м, а одна из диагоналей равна 6 м. Является ли этот параллелепипед прямоугольным? (рис. 5).
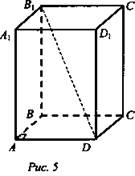
Решение: Предположим, что параллелепипед прямоугольный, тогда в ΔABD: BD2 = АВ2 + AD2, так как ΔABD - прямоугольный и для него справедлива теорема Пифагора. BD2 = 22 + 32 = 13, BD = √13 м. В ΔB1BD, ![]()
![]()
![]() а по условию B1D = 6 м, следовательно, предположение неверно и параллелепипед не является прямоугольным. (Ответ: не является.)
а по условию B1D = 6 м, следовательно, предположение неверно и параллелепипед не является прямоугольным. (Ответ: не является.)
II. Формирование навыков и умений учащихс.
№ 189. Дано: ABCDA1B1C1D1 - куб (рис. 6).
Найти: расстояние от вершины куба до плоскости любой грани, в которой не лежит эта вершина, если:
1) m - диагональ грани;
2) d - диагональ куба.
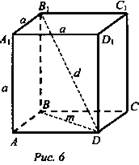
Пусть а - ребро куба (а ребра куба равны), тогда расстояние от вершины А1 (например) до плоскости любой грани будет а (так как ребра куба перпендикулярны).
1. ΔАВС - прямоугольный; ![]()
![]()
2. 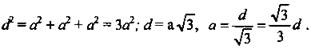 (Ответ:
(Ответ: ![]() )
)
№ 206. Дано: ΔАВС, АВ = 17 см, ВС = 8 см; AС = 15 см, AM ⊥ ABC, АМ = 20 см (рис. 7).
Найти: расстояние от точки М до плоскости ABC.
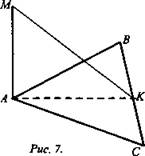
Решение:
1. Проведем АК ⊥ ВС, по теореме о 3-х перпендикулярах МА ⊥ ВС ⇒ МК - искомый отрезок.
2. Применим формулу Герона ![]() С другой стороны,
С другой стороны, ![]()
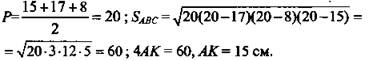
3. ![]() (Ответ: 25 см.)
(Ответ: 25 см.)
№ 207. Дано: МАВС - тетраэдр; АВ = С, ВС = а, AC = b, МО ⊥ AВС; МК = MN = МР = m (рис. 8).
Найти: МО.
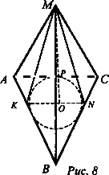
Решение:
1. О - центр вписанной в ΔАВС окружности.
2. Рассмотрим ΔМКО, ΔMNO, ΔМРО; ΔМКО = ΔMNO = ΔМРО (по катету и гипотенузе).
3. Вычислим SΔ и РΔ.
4. Найдем радиус вписанной окружности.
5. ![]() (по теореме Пифагора).
(по теореме Пифагора).
III. Подведение итогов
Домашнее задание
№ 188, 203, 207.