Зачет по теме «Метод координат в пространстве» - Движения - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цель урока:

- проверить теоретические знания учащихся, их умения и навыки применять эти знания в решении задач векторным, векторно-координатным способами.

Ход урока

I. Организационный момент

1. Сообщить тему урока и его цель;

2. Раздать карточки-задания;

3. Пояснить уровень сложности заданий, вошедших в работу (карточку). Каждая карточка содержит три задания: № 1 и № 2 - теоретические, причем № 2 с доказательством; № 3 включает в себя задачу.

Предложены задачи трех уровней сложности: задача № 1 - I уровень; задача № 2 - II уровень и задача № 3 - III уровень.

II. Выполнение работы (по карточкам) (см. приложение)

Домашнее задание

Решение задачи оставшегося уровня (после выбора на зачет), а также задач, содержащихся в карточке соседа по парте (карточки-задания в распечатанном виде выдаются учащимся на дом).

Решение задач вошедших в зачет.

Карточка 1.

№ 1. Дано:

Найдите значение m, при котором будет: а) острым; б) прямым; в) тупым.

Решение: - острый, если - прямой, если - тупой, если при у знак cosy будет зависеть от знака Если 8 + m > 0, m > -8. 8 + m = 0, m = -8. 8 + m < 0, m < -8. (Ответ: а) при m > -8; б) m = -8; в) m < -8.)

№ 2. Дано:

Найти значения k, при которых угол между векторами будет: а) острый; б) прямой; в) тупой.

Решение: Если 7 + 26k > 0, то φ - острый; 7 + 26k = 0, то φ - прямой; 7 + 26k < 0, то φ - тупой. (Ответ: .)

№ 3. Дано: ΔABC; А(m; -3; 2), В(9; -1; 3), С(12; -5; -1) (рис. 1).

Определите значение m, при котором ∠С ΔАВС тупой.

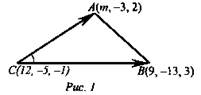
Решение: ∠С - тупой, если cos С < 0. Определим значение m, при котором

(Ответ: при .)

Карточка 2.

№ 1. Дано: А (1; 1; 2), В(0; 1; 1), С(2; -2; 2) и D(2; -3; 1).

Найти: угол между прямыми АВ и CD.

Решение: Рассмотрим направляющие векторы и прямых АВ и CD. (0-1; 1-1; 1-2); (-1; 0; -1). ( 2-2; -13+2; 1-2); (0; -1; -1).

φ = 60°. (Ответ: 60°.)

№ 2. Дано: А(1; 1; 0), В(3; -1; 0), С(4; -1; 2), D(0; 1; 0).

Вычислим угол между прямыми АВ и CD.

Решение:

№ 3. Дано: куб ABCDA1B1C1D1 (рис. 2). Найти: угол между прямыми АВ1 и A1D.

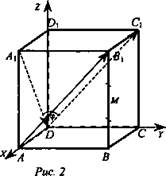
Решение: Введем систему координат Dxyz. Пусть АВ = а, тогда и D(0; 0; 0); С(0; а; 0); А(а; 0; 0); В(а; а; 0). Рассмотрим направляющие векторы и . A1(а; 0; а); В1 (а; а; а); {0; a; a}. {-а; 0; -а}; φ = 60°. (Ответ: 60°.)

Карточка 3.

№ 1. Дано: А(-3; 1; 2), В(1; -1; -2).

Найти: а) координаты середины отрезка АВ; б) координаты и длину отрезка АВ; в) координаты точки С:

Решение:

M - середина АВ; М(-1; 0; 0).

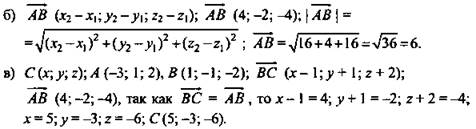
(Ответ:

№ 2. Дано: А(0; 4; 0), В(2; 0; 0), С(4; 0; 4), D(2; 4; 4) (рис. 3).

Доказать, что ABCD - ромб.

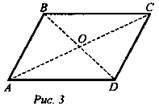
Решение:

1. Докажем, что ABCD - параллелограмм. Для этого воспользуемся признаком параллелограмма. Пусть О - середина АС, O1 - середина BD. О(2; 2; 2); O1(2; 2; 2); O = O1, следовательно, АС ∩ BD = 0 и АО = ОС; ВО = OD; ABCD - параллелограмм.

2. Докажем, что АВ = AD. следовательно, АВ = AD значит, ABCD - ромб (по определению).

№ 3. Дано: А(0; 1; 2), В(√2; 1; 2), С(√2; 2; 1), D(0; 2; 1).

Докажите, что ABCD - квадрат.

Решение: Воспользуемся чертежом задачи № 2.

1) Найдем координаты середин диагоналей четырехугольника ABCD.

- середина АС; - середина BD; O’ = O, следовательно ABCD - параллелограмм.

2) AB = AD ⇒ ABCD - ромб.

3) cледовательно ABCD - квадрат.

Карточка 4.

№ 1. Дано: ΔABC. А(2; 1; -8), B(1; -5; 0), С(8; 1; -4) (рис. 4).

а) Докажите, что ΔABC - равнобедренный;

б) Найти: MN - среднюю линию треугольника, соединяющую боковые стороны.

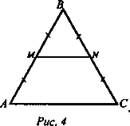
Решение:

1. АВ = ВС ⇒ ΔABC- равнобедренный (по определению).

2. MN - средняя линия или (Ответ: √13.)

№ 2. Дано: ABCD - параллелограмм A(-6; -4; 0), В(6; -6; 2), С(10; 0; 4) (рис. 5).

Найти: D(x; y; z) и угол между

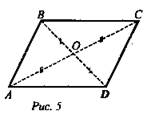
Решение:

1. Найти D(x; y; z); О - середина АС; О - середина BD (по свойству диагоналей параллелограмма). z = 2; D(-2; 2; 2).

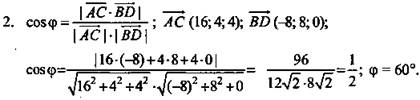
(Ответ: D(-2; 2; 2); 60°.)

№ 3. Дано: A(2; 5; 8), B(6; 1; 0) (рис. 6).

Найдите: a) C(x; y; z); С ∈ Oy; AC = BC; 6) SΔABC.

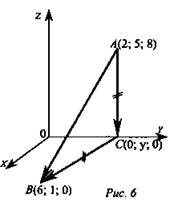
Решение:

а) С ∈ Oy, следовательно, С(0; y; 0); AС = ВС, следовательно, -8y = 37 – 64 - 29; -8y = -56; у = 7, С(0; 7; 0).

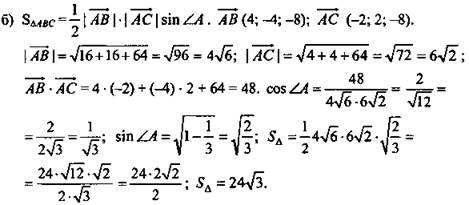
(Ответ: a) С(0; 7; 0), б) SΔ = 24√3.)

Карточка 5.

№ 1. Дано:

Найти:

Решение:

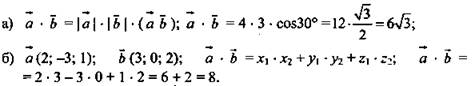
(Ответ: а) 6√3; б) 8.)

№ 2. Дано:

Найти:

Решение:

№ 3. Дано:

Вычислить (Ответ: -20.)

Карточка 6.

№ 1. Дано: М(-4; 7; 0), N(0; -1; 2); K — середина MN (рис. 7).

Найдите: ОК, где О - начало координат.

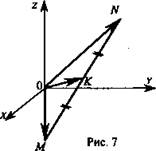
Решение: В ΔOMN ОК — медиана; (Ответ: √14.)

№ 2. Дано: МАВС - тетраэдр; М(2; 5; 7), A(1; -3; 2), В(2; 3; 7), С(3; 6; 0); О - точка пересечения медиан ΔАВС (рис. 8).

Найти: МО.

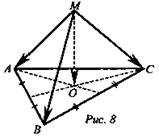
Решение. (Ответ: 5.)

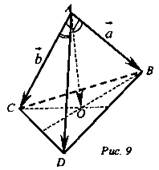
№ 3. Дано: DABC - тетраэдр; DA = 5 см; AB = 4 см; АС = 3 см; ∠BAC = 90°; ∠DAB = 60°; ∠DAC = 45°; О - точка пересечения медиан ΔDBC (рис. 9).

Найти: АО.

Решение:

1.

2. Введем векторы тогда

3. Используем данные задачи на вычисления

4. Подставляем в выражение (Ответ: )