Понятие цилиндра - Цилиндр - ЦИЛИНДР, КОНУС И ШАР

Цепи урока:

- ввести понятия цилиндрической поверхности, цилиндра и его элементов (боковая поверхность, основания, образующие, ось, высота, радиус);

- вывести формулы для вычисления площадей боковой и полной поверхностей цилиндра; рассмотреть типовые задачи по изучаемой теме.

Используемый материал: модели цилиндров, фигур, имеющих цилиндрическую поверхность; плакат с изображением цилиндра, его сечений и развертки.

Ход урока

I. Организационный момент

Объявление темы и цели урока.

II. Актуализация знаний и введение нового материала в форме фронтальной работы с классом по плану

1. Понятие цилиндрической поверхности, цилиндра.

а) Рассмотреть различные предметы окружающей обстановки, дающие представление о цилиндре - карандаш, стакан, кастрюля, кусок трубы и т.д. (Представленные цилиндры должны иметь разные соотношения между высотой и диаметром).

б) Дать определения цилиндрической поверхности, цилиндра и его изображение на плоскости. На чертеже показать ось цилиндра, высоту, радиус, образующие, основания цилиндра. В ходе этой работы использовать плакат, аналогичный рисункам 135 и 136 учебника.

в) Рассмотреть варианты получения цилиндра:

1) путем вращения прямоугольника вокруг прямой, содержащей одну из сторон прямоугольника.

2) по определению цилиндрической поверхности.

2. Ввести понятие осевого сечения цилиндра, установить его свойства:

а) осевое сечение цилиндра — прямоугольник;

б) любые два осевых сечения цилиндра равны между собой. Предложить учащимся самим устно доказать эти свойства.

3. Рассмотреть неосевые сечения цилиндра:

а) сечения, перпендикулярные оси цилиндра, представляют собой равные круги (см. рис. 138 в учебнике),

б) сечения, параллельные оси цилиндра - прямоугольники,

в) сечения иного рода (см. рис. 139 в учебнике).

4. Ввести понятие равностороннего цилиндра, осевым сечением которого является квадрат.

5. Рассмотреть сечения равностороннего цилиндра плоскостью:

а) параллельной оси цилиндра;

б) перпендикулярной оси цилиндра.

6. Ввести понятие касательной плоскости цилиндра как плоскости, проходящей через образующие цилиндра и перпендикулярную осевому сечению, проведенному через эту образующую (аналогия с касательной к окружности).

7. Предложить ребятам ответить на вопрос: что собой представляет развертка цилиндра? Выслушав ответы, рассмотреть готовый чертеж развертки цилиндра (см. рис. 140).

8. Вместе с учащимися вывести формулы боковой поверхности цилиндра, полной поверхности. Формулы выводятся на основе определения, по которому за площадь боковой поверхности цилиндра принимается площадь ее развертки. Тот факт, что боковую поверхность цилиндра можно развернуть на плоскость и при этом получится прямоугольник, принимается на основе наглядных представлений.

где R - радиус основания цилиндра; h - высота цилиндра.

III. Закрепление нового материала

1. Решение задачи по готовому чертежу (устно).

По данному чертежу также потренироваться в названии элементов цилиндра (рис. 1).

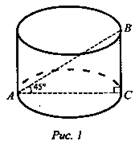
Решение:

1. ΔАВС - прямоугольный.

2. Так как ∠ВАС = 45°, то ΔАВС - равнобедренный, значит, АС = ВС = 5.

3. Так как AС = 5, AС - диаметр, то R = 2,5.

4. где H = 5,

Ответ: 37,5π.

2. Решение задач

№ 525 учебника (рис. 2).

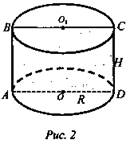
Sсеч. = 10 м2, Sосн. = 5 м2. По условию:

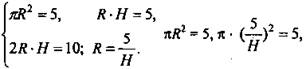
(Ответ: )

№ 529 учебника (рис. 3).

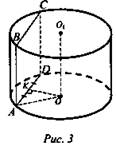
Решение:

1. ABCD - прямоугольник.

2. SABCD = АВ · AD, H = АВ = 8 см.

3. Так как ОК - расстояние от О до AD, то OK ⊥ AD, AK = KD.

4. AD = 8 см.

5. SABCD = 8 · 8 = 64 (см2). (Ответ: 64 см2.)

3. Класс решает задачу № 523 самостоятельно, один ученик решает эту задачу на обратной стороне крыла доски. После окончания решения классу показывается решение ученика (заранее проверенное учителем) для проверки решений в тетрадях (рис. 4).

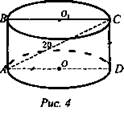
Решение:

1. ABCD - квадрат по условию.

2. H = CD, CD = AD.

3. 2CD2 = AC2 (по теореме Пифагора), CD = 20/√2 = 10√2 (см).

4. (Ответ: 10√2 см, 50π см2.)

Дополнительная задача

В цилиндре параллельно оси проведена плоскость, отсекающая от окружности основания дугу в 60°. Высота цилиндра 10 см, расстояние от оси цилиндра до секущей плоскости 2 см. Найти площадь сечения (рис. 5).

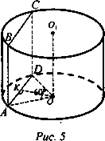
Решение:

1. ABCD - прямоугольник, SABCD = АВ · AD.

2. Н = АВ = 10 см.

3. ∪AD = 60°, значит, ∠AOD = 60° (как центральный), ∠AOK = 30° (ΔAOD - равнобедренный, ОК - высота, медиана и биссектриса).

4.

5. (Ответ: )

IV. Подведение итогов

- Итак, ребята, на этом уроке вы познакомились с понятиями цилиндрической поверхности, цилиндра и его элементами. Вывели формулы для вычисления площадей боковой и полной поверхностей цилиндра и научились применять эти формулы при решении задач.

Домашнее задание

П. 53, 54, № 522, 524, 526.