Координаты вектора - Координаты точки и координаты вектора - МЕТОД КООРДИНАТ В ПРОСТРАНСТВЕ

Цели урока:

- познакомить учащихся с понятием координатных векторов, показать возможность разложения произвольного вектора по координатным векторам

- ввести понятие координат вектора в данной системе координат и отработать навыки действий над векторами с заданными координатами.

Ход урока

I. Организационный момент

Учитель сообщает тему, цель и план урока.

II. Актуализация знаний учащихся

1. Проверка домашнего задания:

а) № 400 (д, е), учащийся готовит решение на доске.

Дано: А(3; -1; 0), В(0; 0; -7), С(2; 0; 0), D(-4; 0; 4), E(0; -1; 0), F(1; 2; 3), G(0; 5; -7), H(-√5; √3; 0).

Указать: д) точки, лежащие в плоскости Oyz\ е) точки, лежащие в плоскости Oxz.

Решение: д) Точки В(0; 0; -7), Е(0; -1; 0), G(0; 5; -7) - лежат в плоскости Oyz, е) Точки В(0; 0; -7), С(2; 0; 0), D(-4; 0; 3) - лежат в плоскости Oxz.

Дополнительные вопросы:

- Как называются координаты точки в пространстве?

- Дать определение вектора.

- Дать определение компланарных векторов.

б) Второй учащийся выполняет у доски задание по карточке.

Начертить прямоугольную трехмерную систему координат и отметить в ней точки А(1; 4; 3), В(0; 5; -3), С(0; 0; 3) и D(4; 0; 6).

Решение (рис. 2):

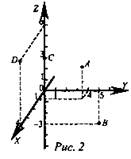
Дополнительные вопросы:

- Как расположена точка относительно прямоугольной системы координат, если ее а) абсцисса равна нулю; б) ордината равна нулю; в) аппликата равна нулю; г) абсцисса и ордината равны нулю?

2. С остальными учащимися класса проводится фронтальный опрос.

Вопросы:

- Как вводится декартова система координат в пространстве?

- При каких условиях говорят, что задана прямоугольная система координат?

- Объясните, как определяются координаты точки в пространстве?

- Используя рисунок (рис. 3 показывается через кодоскоп или готовится на закрытой доске), определить координаты точек А, В, С и D.

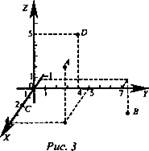
- Как располагаются точки относительно системы координат, если а) одна ее координата равна нулю; б) две ее координаты равны нулю?

Примеры:

- Объясните, почему все точки, лежащие на прямой, параллельной плоскости Оху, имеют одну и ту же аппликату?

- Даны точки А(2; 4; 5), В(3; а; b), С(0; 4; d) и D(5; n; m). При каких значениях а, в, d, n и m эти точки лежат:

а) в плоскости, параллельной плоскости Оху;

б) в плоскости, параллельной плоскости Oxz;

в) на прямой параллельной оси 0x1

Ответ: а) а, n - любые; b = d = 5, б) а = n = 4; b, d, m — любые, в) а = n = 4; b = d = m = 5.

По окончании фронтального опроса просматривается и оценивается работа у доски.

III. Изучение нового материала

1. Учащиеся открывают рабочие тетради, записывают дату и тему урока. Учащиеся в тетради, а учитель на доске, строят прямоугольную систему координат Оху, откладывают от начала координат на осях ох, оу и oz единичные векторы соответственно Их называют координатными векторами (рис. 4).

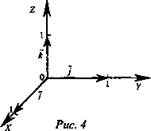
2. Так как векторы некомпланарны, то любой вектор пространства можно разложить в виде где х, у и z определяются единственным образом и являются координатами вектора . Обозначается

Пример: Рассмотрев рисунок 5, где ОА1 = 2, ОА2 = 3, ОА = 3, определите координаты векторов

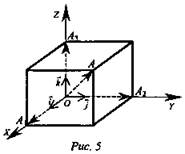
Решение:

Все координаты нулевого вектора равны нулю. Обозначается

Его можно представить в виде:

3. Вводится правило действий над векторами с заданными координатами и доказываются вместе с учителем. (Можно одно правило доказать с учителем, а остальные, группы учащихся доказывают самостоятельно, затем представители группы доказывают у доски. Можно доказательство задать на дом и проверить на следующем уроке.)

1) Равные векторы имеют равные координаты.

Дано:

Доказать: x1 = х2, y1 = у2; z1 = z2.

Доказательство: Так как то так как то b По условию Тогда Откуда x1 - х2 = 0 и х1 = x2; y1 – y2 = 0 и y1 = y2, z1 - z2 = 0 и z1 = z2.

2) Каждая координата суммы двух (и более) векторов равна сумме соответствующих координат этих векторов.

Дано:

Доказать:

Доказательство: Так как то то тогда откуда

3) Каждая координата произведения вектора на число равна произведению соответствующей координаты на это число.

Дано: а - произвольное число;

Доказать:

Доказательство: Так как то Значит,

4) Каждая координата разности двух векторов равна разности соответствующих координат этих векторов.

Дано:

Доказать:

Доказательство: тогда - Тогда

IV. Закрепление изученного материала

На закрытой доске заранее подготовлено задание для устной работы.

1. Даны векторы

1) Разложить их по координатным векторам.

2) Найти вектор равный

2. Дано: Укажите координаты векторов

V. Формирование знаний, умений и навыков учащихся

Задачи № 403 и № 404 (по 2 примерам) по 2 человека для контроля решают у доски, а класс решает самостоятельно, затем сверяется с решением у доски. Учитель в это время контролирует работу у доски.

Задача № 403.

тогда

тогда

Задача № 404.

тогда

тогда

Аналогично выполняется №407. У доски 1-й учащийся выполняет пункты а, б, в, 2-й - г, д, е.

Учитель в это время контролирует работу слабых учащихся и проверяет работу у доски.

Задача № 407.

Дано:

Найти: Решение.

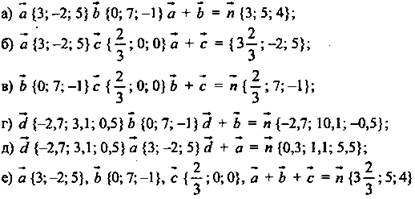
VI. Итог урока

- Сегодня на уроке мы изучили понятие координационных векторов и рассмотрели разложение произвольного вектора по векторам Также мы изучили понятие координат вектора и правила действий над векторами.

Домашнее задание

П. 43 (или теорию по тетради), повторить определение средней линии треугольника и теорему о средней линии треугольника. № 403, 404, 407 (оставшиеся пункты).