Поурочные разработки по Геометрии 11 класс
Объем наклонной призмы - Объем наклонной призмы, пирамиды и конуса - ОБЪЕМЫ ТЕЛ
Цели урока:
- вывести формулу объема наклонной призмы с помощью интеграла;
- показать применение полученной формулы для решения задач;
- сформировать навык по нахождению объема наклонной призмы.
Ход урока
I. Организационный момент
Проверка домашнего задания. Вывод формулы у доски.
II. Теорема об объеме наклонной призмы
Объем наклонной призмы равен произведению площади основания на высоту.
Доказательство:
Рис. 1 на слайде (или ватм. лист).
![]()
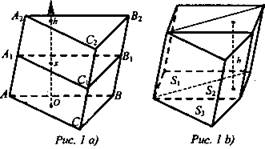
1) Рассмотрим треугольную призму с объемом V и площадью основания S, высотой h.
Точка О принадлежит одному из оснований призмы, направим ось ох перпендикулярно основаниям. Рассмотрим сечение призмы плоскостью, перпендикулярной к оси ох и, значит, параллельно плоскости основания.
х - абсцисса точки пересечения этой плоскости с осью ох, площадь полученного сечения - S(x).
ΔАВС (основание призмы) = ΔА1В1С1 (сечение призмы), так как AА1В1В - параллелограмм ![]()
Аналогично: ![]() значит, равенство треугольников вытекает по 3 признаку (3 стороны);
значит, равенство треугольников вытекает по 3 признаку (3 стороны);
S(x) = S.
По основной формуле:
![]()
2) Докажем для любой призмы с высотой h и площадью основания S.
Разбиваем призму на 3 призмы с общей высотой h. Выразим объем каждой призмы и сложим их. Вынося h за скобки, получаем сумму площадей оснований 3-угольных призм, т.е. площадь основания исходной призмы. Имеем: V = S · h.
III. Решение задач: № 682,680, 676.
Дома: п. 68, № 681, 683.
Решение задач у доски.
Задача № 676.
Найти объем наклонной призмы, у которой основанием является треугольник со сторонами 10 см, 10 см, 12 см, а боковое ребро равное 8 см, составляет с плоскостью основания угол 60°.
Дано: АВСА1В1С1 - наклонная призма, АВ = 10 см, ВС = 10 см, АС = 12 см, ВВ1 = 8 см, ∠B1BK = 60° (рис. 2).
Найти: Vnp. - ?

Решение.
1) ![]() (ф-ла Герона).
(ф-ла Герона). ![]()
2) ΔBB1H - прямоугольный, так как В1Н - высота. В1Н = ВВ1 · sin60°; ![]()
3) ![]()
(Ответ: Vnp. = 192√3 см3.)
Задача № 680.
Основанием наклонной призмы является прямоугольник со сторонами а и b. Боковое ребро длины с составляет со смежными сторонами основания углы, равные φ. Найти объем призмы.
Дано: АВСDА1В1С1D1 - призма, ABCD - прямоугольник, АВ = а, AD = b, АА1 = с. ∠A1AD = ∠A1AB = φ (рис. 3).
Найти: Vnp.
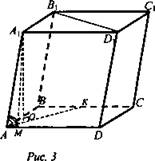
Решение:
1) ∠A1AD = ∠A1AB, значит, точка А1 проецируется на биссектрису ∠А. А1O ⊥ (ABC), АО - биссектриса ∠A.

3) ΔAA1M - прямоугольный, АМ = С · соsφ.
4) ΔАОМ - прямоугольный, ![]()

(Ответ: ![]() )
)
Задача № 682.
Объем наклонной призмы равен произведению бокового ребра на площадь сечения призмы, плоскостью, перпендикулярной к боковым ребрам и их пересекающей.
Или ![]() перпендикулярного ему сечения (рис. 4).
перпендикулярного ему сечения (рис. 4).
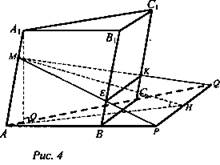
Доказательство:
1) (МЕК) - плоскость перпендикулярного сечения призмы, (ABC) - плоскость основания. (МЕК) ∩ (ABC) по прямой PQ. АА1 ⊥ (МЕК), ⇒ АА1 ⊥ PQ.
2) Проведем высоту А1О - призмы, А1О ⊥ PQ.
3) 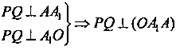 (по признаку перпендикулярности прямой и плоскости).
(по признаку перпендикулярности прямой и плоскости).
4) (АА1О) || PQ в точке Н, ∠AHM - линейный угол двугранного угла ∠QPM. ∠AHM = φ, тогда ∠MAH = 90° - φ.
5) ΔМЕК - ортогональная проекция ΔАВС на плоскость перпендикулярного сечения. ![]()
6) (APQ) ⊥ (АМН), так как (APQ) проходит через PQ, перпендикулярно (АМН).
7) Из ΔАА1O: ![]()
8) ![]()
Что и требовалось доказать.
Произвольная призма состоит из треугольных призм, следовательно, ![]()
IV. Групповая работа по готовым чертежам
Оценивается работа всей группы, задаются теоретические вопросы в качестве проверки знания теоретического материала и дополнительного задания.
1. Дано: ВВ1С1С - ромб, B1С ⊥ (ABC), В1С = 3, ΔАВС - равносторонний, ВВ1 = 5 (рис. 5).
Найти: Vnp.
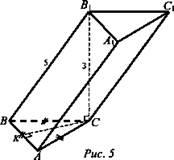
Решение:
1) ![]() (по условию).
(по условию).
2) ![]()
![]()
3) ∠B1CK = 90° (по определению угла между прямой и плоскостью); В1С = 3. ![]() (Ответ:
(Ответ: ![]() )
)
2. Дано: АВ = АС = 3 см; ВС = 2 см; АА1 = 4 см; ∠А1АН = 45°. Vnp. = Vкуба. (рис. 6).
Найти: а - ребро куба.
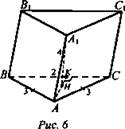
Решение:
1) ![]() по формуле Герона;
по формуле Герона; ![]()
2) AK ⊥ BС; M ∈ АК; ΔАА1Н - прямоугольный, ![]()

(Ответ: а = 2 см.)
3. Дано: ABCDA1B1C1D1 - призма; ABCD - прямоугольник; АВ = 6 см; AD = 8 см, AA1B1B - квадрат; ∠KHF = 60° (рис. 7).
Найти: Vnp - ?
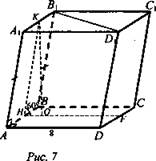
Решение:
1. ![]()
![]()
2. КО - высота призмы; ΔКОН - прямоугольный, ![]()
![]()
3. ![]()
(Ответ: 144√3 см3.)
V. Подведение итогов
- Напишите формулу для определения объема наклонной призмы.
Проверка решений задач;
Выставление оценок.