Поурочные разработки по Геометрии 11 класс
Решение задач на нахождение объема конуса - Объем наклонной призмы, пирамиды и конуса - ОБЪЕМЫ ТЕЛ
Цели урока:
- закрепить знания и умения по теме «Объем конуса»;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
1. Проверка домашнего задания: у доски - № 708, дополнительная задача, вывод формулы Vk и Vус.к.; с места - № 701, 704.
2. Решение задач по готовым чертежам.
3. Решение задач у доски и в рабочих тетрадях.
III. Самостоятельная работа с последующей самопроверкой
IV. Подведение итогов
1. Записать домашнее задание.
П. 70, № 702, 705, 703.
Домашняя контрольная работа (см. приложение)
Дети получают ксерокопии домашних контрольных задач.
1. Проверка домашнего задания.
Задача № 701. Пусть h, r и V соответственно высота, радиус основания и объем конуса. Найдите: а) V, если h = 3 см, r = 1,5 см; б) h, если r = 4 см, V = 48π см3; в) r, если h = m, V = p.
Решение:
a) ![]() (Ответ: V = 2,25π см3.)
(Ответ: V = 2,25π см3.)
б) из формулы ![]() (Ответ: h = 9 см.)
(Ответ: h = 9 см.)
в) из формулы ![]() (Ответ:
(Ответ: ![]() )
)
Задача № 708. Радиусы оснований усеченного конуса равны 3 м и 6 м, а образующая равна 5 м. Найдите объем конуса.
Дано: усеченный конус, r = О1С = 3 м, ОВ = R = 6 м, СB = 5 м (рис. 1).
Найти: Vус.п.
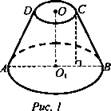
Решение: ![]() Проведем СС1 ⊥ АВ, O1С = OС1 = 3 м, C1B = 6 - 3 = 3 (м). Из ΔСВС1 (∠C1 = 90°) по теореме Пифагора
Проведем СС1 ⊥ АВ, O1С = OС1 = 3 м, C1B = 6 - 3 = 3 (м). Из ΔСВС1 (∠C1 = 90°) по теореме Пифагора ![]() отсюда
отсюда ![]()
![]()
![]()
Задача № 704. Дано: конус, h = SO = AB = H (рис. 2).
Найти: V.
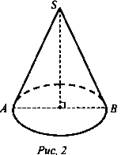
Решение: ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Дополнительная задача: Равносторонний треугольник вращается вокруг своей стороны а. Найдите объем полученного тела вращения.
Дано: ΔАВС, АВ = ВС = АС = а, АС - ось вращения (рис. 3).
Найти: объем тела вращения.
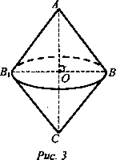
Решение: Объем тела вращения равен сумме объемов двух равных конусов. ![]()
![]() (из ΔAOB (∠O = 90°) по теореме Пифагора
(из ΔAOB (∠O = 90°) по теореме Пифагора ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Заслушать учащихся, выводивших формулы для Vк и Vус.к..
2. Решение задач по готовым чертежам.
№ 1. Установите соответствие фигур и формул для нахождения объема (рис. 4 а), б), в)).
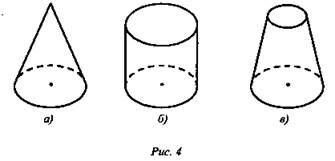
![]()
№ 2. Образующая конуса равна 60 см, высота 30 см. Найдите Vк (рис. 4).
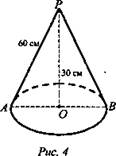
Решение: Из ΔАOР (∠O = 90°): Так как РО = 1/2АР, то ![]()
![]() (Ответ: V = 27000π см3.)
(Ответ: V = 27000π см3.)
№ 3. Образующая конуса, равна 12 см, наклонена к плоскости основания под углом 30° (рис. 5).
Найдите объем конуса.
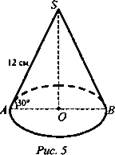
Решение: ![]() Из ΔАSO (∠O = 90°):
Из ΔАSO (∠O = 90°): ![]()
![]() (Ответ: V= 216π см3.)
(Ответ: V= 216π см3.)
№ 4. Радиус оснований усеченного конуса 6 см и 10 см. Образующая наклонена к плоскости большего основания под углом 60°.
Найдите: Vус.к..
Дано: α = 60°, R = 10 см, r = 6 см (рис. 6).
Найти: Vус.к..
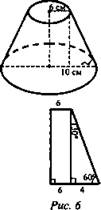
Решение: ![]()
![]() (Ответ:
(Ответ: ![]() )
)
№ 5. Образующая конуса 8 см, а угол при вершине осевого сечения 60°.
Найдите объем конуса.
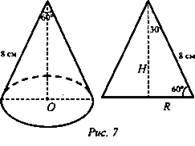
Решение: (рис. 7): ![]()
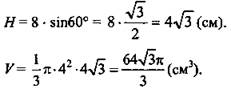 (Ответ:
(Ответ: ![]() )
)
№ 6. Найдите объем усеченного конуса, если его осевое сечение трапеция с основаниями 8 см, 6 см и высотой 3 см (рис. 8).
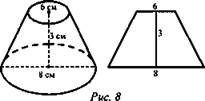
Решение: ![]()
![]()
![]() (Ответ: V = 37π см3.)
(Ответ: V = 37π см3.)
3. Решение задач у доски и в рабочих тетрадях.
№ 1. Доказать, что если прямой круговой конус пересечь плоскостью, параллельной основанию, то площади сечения и основания будут относиться как квадраты их расстояний от вершины.
Дано: конус, S - площадь основания, S1 - площадь сечения (рис. 9).
Доказать: ![]()
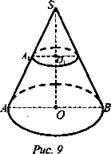
Решение: Сечением прямого кругового конуса плоскостью, параллельной основанию, является круг. Осевым сечением конуса является равнобедренный треугольник.
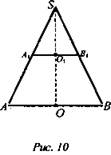
Из подобия ΔASB и ΔA1S1B1 (рис. 10) находим ![]() следовательно,
следовательно, ![]()
Что и требовалось доказать.
(Ответ: задача доказана.)
№ 2. Разность между образующей конуса и его высотой равна d, а угол между ними равен α. Найдите объем конуса.
Дано: конус, SO - высота, SB - образующая. SB - SO = d, ∠BSO = α (рис. 11).
Найти: V.
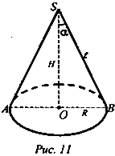
Решение: ![]() Из ΔSOB (∠O = 90°):
Из ΔSOB (∠O = 90°): ![]() По условию SB - SO = d. Имеем
По условию SB - SO = d. Имеем ![]() Итак,
Итак, ![]()
(Ответ: ![]() )
)
№ 3. Усеченный конус, у которого R1 = 22 см, R2 = 4 см, требуется превратить в равновеликий цилиндр такой же высоты. Чему равен радиус основания этого цилиндра?
Дано: цилиндр, усеченный конус, R1 = 22 см, R2 = 4 см, Vц. = Vк.
Найти: R (радиус цилиндра).
Решение: Н - общая высота тел, R - радиус цилиндра. Vц. = Vк., ![]()
![]() (Ответ: R = 14 см.)
(Ответ: R = 14 см.)
Самостоятельная работа (см. приложение)
Ответы к задачам самостоятельной работы:
Вариант I. V = 24π см3. V = 9π м3
Вариатн II. ![]()
![]()
Решение самостоятельной работ.
Вариант 1
№ 1. ![]() Из ΔCBD (∠D = 90°);
Из ΔCBD (∠D = 90°); ![]() Из ΔSCB:
Из ΔSCB: ![]()
![]() Из ΔSOB (∠O = 90°):
Из ΔSOB (∠O = 90°): ![]() (Ответ: V = 24π см3.)
(Ответ: V = 24π см3.)
№ 2. Дано: конус, ΔАРВ - осевое сечение, АР = РВ, ∠P = 90°. SΔAPB = 9 м2 (рис. 14).
Найти: Vк.
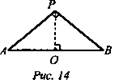
Решение: ![]() Н = РО, R = АО,
Н = РО, R = АО, ![]() l - образующая конуса, ∠A + ∠B = 90°, ∠A = ∠B = 45°. Из ΔАРО (∠O = 90°): ∠APO = ∠PAO = 45°, значит, AO = PO = R = H.
l - образующая конуса, ∠A + ∠B = 90°, ∠A = ∠B = 45°. Из ΔАРО (∠O = 90°): ∠APO = ∠PAO = 45°, значит, AO = PO = R = H. ![]() По теореме Пифагора
По теореме Пифагора ![]()
![]() (Ответ: V = 9π м3..
(Ответ: V = 9π м3..
Вариант II
№ 1. Дано: усеченный конус, ВВ1 = 6 см, ∠BAB1 = 30°, ∠AB1B = 90° (рис. 15).
Найти: Vус.к..
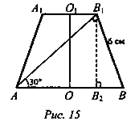
Решение: ![]() АВ = 12 см, R = ОВ = 6 см, ∠ABB1 = 60°. Проведем В1В2 ⊥ АВ. Из ΔBB1B2 (∠B2 = 90°): ∠B1 = 30°, значит, ВВ2 = 3 см, тогда,
АВ = 12 см, R = ОВ = 6 см, ∠ABB1 = 60°. Проведем В1В2 ⊥ АВ. Из ΔBB1B2 (∠B2 = 90°): ∠B1 = 30°, значит, ВВ2 = 3 см, тогда, ![]()
![]() (Ответ:
(Ответ: ![]() )
)
Решение домашней работы
№ 702. Дано: конус, РО = 5 см, РО1 = 2 см, V1 = 24 см3 (рис. 16).
Найти: Vк..
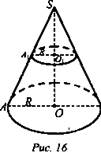
Решение: Н = РО - высота конуса, V1 – объем меньшего конуса, АО = R, A1O1 = R. ΔРО1А1 ~ ΔРОA, тогда, ![]()
![]()
![]() (Ответ: V = 375 см3.)
(Ответ: V = 375 см3.)
№ 705. Дано: конус, ΔASB - осевое сечение, SΔASB = 60 см2, SB = SA = 13 см (рис. 17).
Найти: Vк..
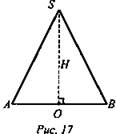
Решение: ![]() Из ΔSOB (∠O = 90°):
Из ΔSOB (∠O = 90°): ![]()
![]() Из (1) и (2):
Из (1) и (2): ![]()
тогда ![]() При R = 5, H = 12, тогда
При R = 5, H = 12, тогда ![]() (Ответ: 240π см3 или 100π см3.)
(Ответ: 240π см3 или 100π см3.)
№ 703. Дано: конус, Sосн. = Q, Sбок. = Р (рис. 18).
Найти: Vк..
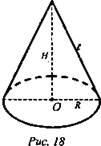
Решение: ![]() где R - радиус основания, H - высота.
где R - радиус основания, H - высота. ![]() l - образующая,
l - образующая, 
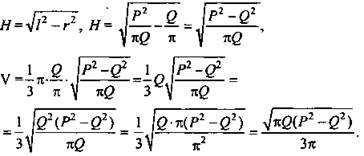
(Ответ: ![]() )
)
Решение домашней контрольной работ.
№ 1. Дано: ΔАВС, АС = ВС = a, ∠C = α. l || СВ, l - ось вращения (рис. 19).
Найти: объем полученного тела вращения.
Решение: Проведем CL || l и ВK ⊥ l, тогда Vтела = Vu – V1 - V2, где Vu – объем цилиндра, полученного вращением прямоугольника KBCL, V1 и V2 - объемы конусов, образующихся вращением ΔАКВ и ΔALC. ![]()
![]() так как LC = КВ, a BC = AK + AL, то
так как LC = КВ, a BC = AK + AL, то ![]()
![]() ВС = а, Из ΔALC (∠L = 90°) : LC = asinα, поэтому
ВС = а, Из ΔALC (∠L = 90°) : LC = asinα, поэтому ![]() (Ответ:
(Ответ: ![]() )
)
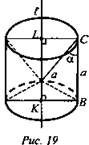
№ 2. Дано: конус, АР = √6 см, ∠PAB = 45° (рис. 20).
Найти: V.
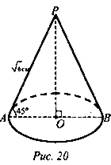
Решение: ![]() R = AO, H = РО. Из ΔAОР ((∠O = 90°): ∠APO = 45°, значит, AO = PO = R=H. По теореме Пифагора 2R2 = 6, R2 = 3, R = H = √3.
R = AO, H = РО. Из ΔAОР ((∠O = 90°): ∠APO = 45°, значит, AO = PO = R=H. По теореме Пифагора 2R2 = 6, R2 = 3, R = H = √3. ![]() (Ответ: V = π√3 см3.)
(Ответ: V = π√3 см3.)
№ 3. Дано: цилиндр, конус, ОВ = O1В1 = 2,5 м, SO1 = 4 м, ОО1 = 2,2 м, ρ = 0,03 г/см3 (рис. 21).
Найти: m.
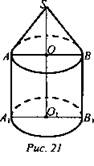
Решение: ![]() где
где ![]()
![]()
![]()
![]() (Ответ: 1,6 т - масса стога сена.)
(Ответ: 1,6 т - масса стога сена.)
№ 4. Дано: конус, R - радиус основания, усеченный конус, R - радиус основания (рис. 22).
Найти: ![]()
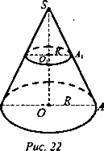
Решение: ![]()
![]() ΔSA1O1 ~ ΔSAO, значит,
ΔSA1O1 ~ ΔSAO, значит, ![]() отсюда
отсюда ![]()
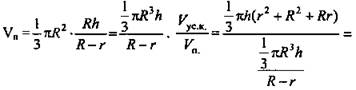
![]() (Ответ:
(Ответ: ![]() )
)
№ 5. Дано: два конуса, O1 = О - центры оснований, ∠ASO = ∠A1S1O1 = α, ОА = R. Sбок.внут. < Sполн.внеш. в 2 раза (рис. 23).
Найти: Vвнутр.к.
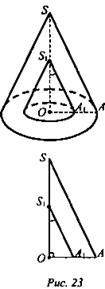
Решение: Из ΔS1OA1 (∠O = 90°): ![]()
![]() Из ΔSOA (∠O = 90°):
Из ΔSOA (∠O = 90°): ![]()

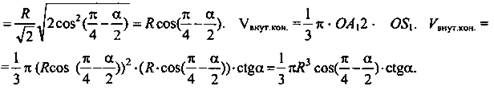
(Ответ: ![]() )
)