Поурочные разработки по Геометрии 11 класс
Объем шарового сегмента, шарового слоя и шарового сектора - Объем шара и площадь сферы - ОБЪЕМЫ ТЕЛ
Цели урока:
- систематизировать знания умения и навыки по данной теме;
- совершенствовать навыки решения задач на применение формул для вычисления объемов частей шара.
Ход урока
I. Организационный момент
II. Актуализация знаний учащихся
1. Теоретический опрос. Фронтальная работа с классом.
(В этот момент два ученика кратко записывают решение домашнего задания № 720, 715).
- Дать определение шарового сегмента.
- Записать формулу объема шарового сегмента.
- Дать определение шарового слоя. Записать формулу нахождения объема шарового слоя.
- Дать определение шарового сегмента. Записать формулу объема шарового сегмента.
После обсуждения вопросов заслушать ответы учеников, работавших у доски.
Задача № 720 (рис. 1).
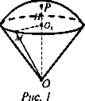
Решение: Пусть R - радиус шара, r - радиус основания сегмента. Вычислим высоту сегмента Н = РО1, OP = R. Из прямоугольного ΔОО1М: ![]()
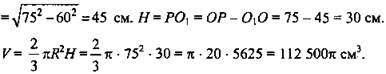
Задача № 715 (рис. 2).
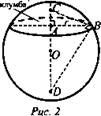
Пусть АС = А, АВ = r, r - радиус клумбы, примем радиус шара равным RMX. Рассмотрим центральное сечение шара. CD = 2R, ∠CBD = 90°, так как он опирается на диаметр CD. Из ΔCDB: СВ = 2Rcosα, из ΔАСВ: ![]() Получим уравнение:
Получим уравнение:
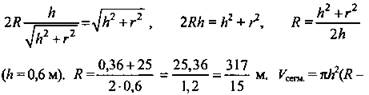
![]() (Ответ:
(Ответ: ![]() )
)
III. Решение задач на формирование умений и навыков учащихся
1. Плоскость, перпендикулярная диаметру шара, делит его на части 3 см и 9 см. На какие части делится объем шара?
Решение: R = (3 + 9) : 2 = 6 см. Высота меньшего сегмента h равна 3 см. Его ![]() Значит,
Значит, ![]()
2. Найти отношение сегментов из предыдущей задачи.
(Ответ: ![]() ).
).
3. Какую часть шара составляет объем шарового сегмента, у которого высота равна 0,1 диаметра шара?
Решение: Десятая часть диаметра есть пятая часть радиуса. Значит, высота сегмента ![]()
![]() (Ответ: 2,8%.)
(Ответ: 2,8%.)
IV. Самостоятельная работа (см. приложение)
Ответы:
I уровень: 1) 5/27; 2) ![]()
II уровень: 1) 6 см; 2) ![]()
III уровень: 1) объем шара больше; 2) 3528π см3.
V. Подведение итогов
- Покажите на чертеже шаровой слой и шаровой сегмент.
Собрать тетради учащихся для проверки самостоятельной работы.
Домашнее задание № 917, 756.
Дополнительная задача
Диаметр основания конуса равен 6 м, образующая наклонена к плоскости основания под углом 60° (рис. 3).
Найти: объем шара описанной около конуса сферы.
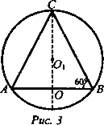
Решение:
1) Центр O1 ∈ ОС, ∠OBC = 60° ⇒ ΔАВС - равносторонний.
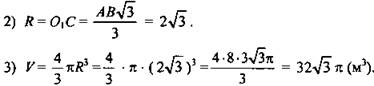 (Ответ:
(Ответ: ![]() )
)