Поурочные разработки по Геометрии 11 класс
Аксиомы стереометрии. Повторение - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цель урока:
- повторение аксиом и следствий из них, применение к решению задач.
Ход урока
I. Повторение теоретического материала
Вопросы:
1) Сформулировать аксиомы стереометрии и выполнить на доске ил люстрации к каждой из них (рис. 1 а), б), в)).
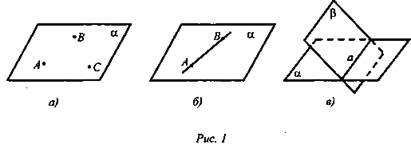
2) Сформулировать следствия из аксиом и выполнить на доске иллюстрации к ним.
Теорема: Через прямую и не лежащую на ней точку проходит плоскость, и притом только одна.
Теорема: Через две пересекающиеся прямые проходит плоскость, и притом только одна (рис. 2).
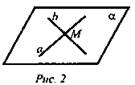
3) Какие аксиомы используются при доказательстве I следствия? (Ответ: A1; А2)
4) Какие аксиомы используются при доказательстве II следствия? (Ответ: А2.)
II. Решение задач на готовых чертежах (рис. 3).

Дано: точки А, В, С и D не лежат в одной плоскости.
Указать:
1) плоскости, которым принадлежит: а) прямая АВ; б) точка F; в) точка С.
2) прямую пересечения плоскостей: a) ABC и ACD; б) ABD и DCF.
Дано: точка D лежит вне плоскости ABC. Пересекаются ли прямые DE и ВС? (рис. 4).
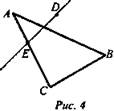
(Ответ: нет. Воспользоваться методом доказательства от противного.)
III. Решение задач
№ 1. Даны две различные прямые, пересекающиеся в точке А. Докажите, что все прямые, пересекающие обе данные прямые и не проходящие через точку А, лежат в одной плоскости (рис. 5).
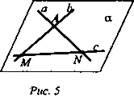
Решение: Проведем через данные прямые а и b плоскость α (следствие из аксиом). Прямая с, пересекающая данные прямые имеет с плоскостью а две общие точки М и N (точки пересечения с данными прямыми). По аксиоме А2 эта прямая должна лежать в плоскости α.
№ 2. Докажите, что все прямые, пересекающие данную прямую и проходящие через данную точку вне прямой, лежат в одной плоскости (рис. 6).
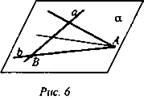
Решение: Данная прямая а и точка А определяют плоскость α (следствие из аксиом). Если прямая b проходит через точку А и пересекает прямую а в точке В, то прямая b имеет с плоскостью α две различные общие точки (А и В) и поэтому лежит в указанной плоскости α (А2).
№ 3. Даны четыре точки. Известно, что прямая, проходящая через любые две из этих точек, не пересекается с прямой, проходящей через другие две точки.
Докажите, что данные четыре точки не лежат в одной плоскости.
Решение: П, точки Л, В, С и D лежат в одной плоскости. Тогда прямые АВ и CD, АС и BD были бы параллельными, так что точки А, В, С, D являлись бы вершинами параллелограмма ABCD. Однако диагонали AD и ВС этого параллелограмма должны пересекаться, что противоречит условию задачи.
IV. Подведение итогов
Заполните пропуски, чтобы получилось верное утверждение:
а) если А ∈ α, а ∈ α, то A...α;
б) если А ∈ α, В ∉ α, то АВ...α;
в) если А ∈ α, В ∈ α, С ∈ АВ, то С...α;
г) если М ∈ α, М ∈ β, а ∩ β = а, то М...α.
Домашнее задани.
а) п. 1-3 учебника.
б) № 9; 15.
I уровень
№ 9 (рис. 7).
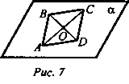
Решение: А, В, О ∈ α. Из того, что А, О ∈ α, по A2 следует, что С ∈ α (ибо С ∈ АО). Из того, что В, О ∈ α, по A2 следует, что D ∈ α (ибо D ∈ ВО). Итак, С и D лежат в плоскости α.
(Ответ: да.)
II уровень
№ 15 (рис. 8).
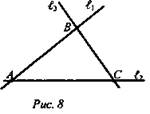
Решение: Каждая из трех точек принадлежит сразу двум прямым. Например, через АВ и С ∈ АВ по теореме п. 3 можно провести единственную плоскость α. Это значит, что все три отрезка АВ, ВС и АС лежат в плоскости α (аксиома А2), поэтому прямые, которым принадлежат эти отрезки, также ∈ α.
Другой случай (рис. 9).
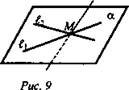
L1, l2 ⊂ α, но l3 ⊄ α, хотя и пересекается с l2 и l1 в точке М.