Поурочные разработки по Геометрии 11 класс
Многогранники: параллелепипед, призма, пирамида, площади их поверхностей - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цели урока:
- систематизировать теоретические знания по теме;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
Повторение материала в ходе устного опроса.
1. Определение многогранника, его элементов.
2. Что такое геометрическое тело?
3. Секущая плоскость - это ...
4. Определение призмы, прямой призмы, наклонной призмы, правильной призмы. Формулы площади полной поверхности призмы, боковой поверхности призмы.
5. Формула объема призмы.
6. Определение пирамиды, правильной пирамиды, усеченной пирамиды. Формулы площади полной поверхности, боковой поверхности пирамиды.
7. Объем пирамиды (формула).
Проверка домашнего задания.
Задача № 212 (рис. 1).
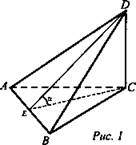
1) DС ⊥ пл. AВС по условию, DC ⊥ AB. Проводим СЕ ⊥ АВ, по теореме о трех перпендикулярах DE ⊥ AB. ∠DEC - линейный угол двугранного угла CABD, пусть ∠DEC = α.
2) Пусть ![]()
![]()
![]()
Утверждение доказано.
Задача № 216 (рис. 2)
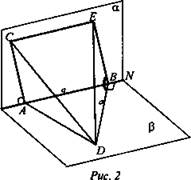
Решение:
1) Построим линейный угол двугранного угла. Проведем BE ⊥ MN, соединим точки Е и D, проведем CE || AB. ![]() - линейный угол двугранного угла CMND.
- линейный угол двугранного угла CMND.
2) АСЕВ - квадрат, BE = а. Из ΔBDE по теореме косинусов: ![]()
![]()
3) ![]() ⊥ пл. DBE, CE ⊥ DE, ∠CED = 90°. Из прямоугольного ΔCED:
⊥ пл. DBE, CE ⊥ DE, ∠CED = 90°. Из прямоугольного ΔCED: ![]() (Ответ: 2а.)
(Ответ: 2а.)
III. Решение задач
№ 294. Задачу решить самостоятельно, с последующей проверкой на доске (рис. 3)..
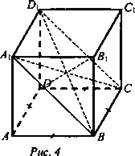
Решение: Правильная четырехугольная призма - частный случай прямоугольного параллелепипеда (диагонали которого пересекаются в одной точке и делятся в ней пополам). В сечении A1D1CB - прямоугольник, его площадь S0. S0 = а · A1B, следовательно, ![]() Из прямоугольного ΔА1АВ.
Из прямоугольного ΔА1АВ.
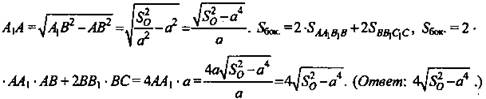
№ 300 (рис. 4).
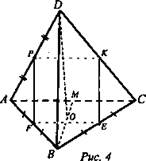
Решение:
1) Построим сечение плоскостью, проходящей через точки Е, F и Р. Проводим EF в пл. ABC. EF - средняя линия в ΔАВС. EF || AC, ![]()
2) EF || AC, АС ⊂ пл. DCA, значит EF || пл. DCA. Плоскость сечения пересечет грань DCA по некоторой прямой РК. По теореме, если плоскость сечения проходит через прямую (EF), параллельную другой плоскости (DCA), и пересекает эту плоскость (DCA), то линия пересечения (РК) параллельна первой прямой (EF). Следовательно, EF || PK. Проводим в грани BDA отрезок FP, а в грани BDC отрезок ЕК. Четырехугольник EFPK - искомое сечение. EF || AC, PK || EF || AC, ![]() Значит,
Значит, ![]() Из того, что EF || PK и EF = РК, следует, что EFPK - параллелограмм. Т. е., EK || FP, ЕК - средняя линия ABCD,
Из того, что EF || PK и EF = РК, следует, что EFPK - параллелограмм. Т. е., EK || FP, ЕК - средняя линия ABCD, ![]()
Докажем, что угол между скрещивающимися прямыми DB и СА равен 90°. Проведем высоту пирамиды DO. Точка О - центр правильного ΔABC. Продолжим отрезок ВО до пересечения со стороной АВ в точке М. В правильном ΔABC отрезок ВМ - высота, медиана и биссектриса, значит, BM ⊥ CA. Итак, BM ⊥ CA, DO ⊥ CA. По признаку перпендикулярности прямой и плоскости, СA ⊥ пл. BDM, значит, CA ⊥ BD.
Вывод: раз СА ⊥ BD, а РК || СА и ЕК || BD, то РК ⊥ ЕК и четырехугольник EFPK становится прямоугольником. ![]() (Ответ: 1/4ab.)
(Ответ: 1/4ab.)
№ 307 (рис. 5).
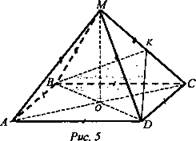
Решение:
1) Построим сечение пирамиды плоскостью α, параллельной МА и проходящей через BD. Проведем в пл. АМС отрезок ОK || АМ, отрезки DK и ВК. АМ || ОК, OK ⊂ BKD, значит, АМ || пл. BDK, пл. BDK есть искомая плоскость α. АО = ОС, ОK || АМ, значит, ОК - средняя линия ΔАМС, OK = 1/2b. ABCD квадрат, поэтому диагональ BD = a√2. ![]() так как OK ⊥ BD (AC ⊥ BD, MO ⊥ BD - значит, пл. AMC ⊥ BD, тогда, OK ⊥ BD).
так как OK ⊥ BD (AC ⊥ BD, MO ⊥ BD - значит, пл. AMC ⊥ BD, тогда, OK ⊥ BD). ![]()
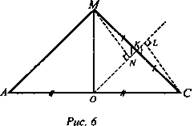
2) Докажем, что точки М и С равноудалены от пл. α. ОК - средняя линия ΔАМС, МК = КС (рис. 6). Проведем MN ⊥ OK и CL ⊥ OK, BD ⊥ пл. АМС, значит, BD ⊥ MN и BD ⊥ CL, тогда, MN ⊥ пл. BDK и CL ⊥ пл. BDK, MN и CL и есть расстояние от точек М и С до пл. α. ΔMNK = ΔLCK (по гипотенузе и острому углу). Итак, MN = CL (рис. 6). (Ответ: ![]() )
)
IV. Подведение итогов
- Назовите формулы для определения полной поверхности а) призмы; б) пирамиды.
Домашнее задание
№ 308, 318.
Краткий анализ домашнего задания.
№ 308. а) дополнительные построения: OK ⊥ DC, OL ⊥ AD; отрезки KS и LS; б) рассмотреть ΔSOL и ΔSOK. Доказать равенство высот боковых граней. в) Найти OL и SL.
№ 318. а) произвести отсечение от вершины данного тетраэдра - правильный тетраэдр с ребром а; б) рассмотреть октаэдр; в) рассмотреть двугранные углы между плоскостями; г) перейти к линейным углам.