Поурочные разработки по Геометрии 11 класс
Многогранники: параллелепипед, призма, пирамида - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цель урока:
- проверка использования теоретических знаний и практических навыков при решении задач по данной теме.
Ход урока
I. Организационный момент
Сообщить тему урока, сформулировать цели урока.
II. Актуализация знаний учащихся
Проверка домашнего задания по ранее заготовленному решению.
Задача № 308 (рис. 1).
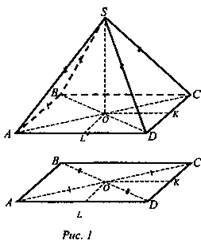
Решение: Проводим OK ⊥ DC, OL ⊥ AD, отрезки KS и LS. По теореме о трех перпендикулярах SK ⊥ DC и SL ⊥ AD. Меньшая диагональ - BD, так как она лежит против острого угла ромба. ΔLOD = ΔKOD, поэтому OL = ОК. Значит, ΔSOL = ΔSOK. SK = SL. Таким образом, высота всех четырех боковых граней равна. Из ΔAOD по теореме Пифагора: ОА = 4 (см), ![]()
![]() Из ΔODL: OL = 2,4 (см), так как
Из ΔODL: OL = 2,4 (см), так как ![]() Из ΔSOL:
Из ΔSOL: ![]()
![]() (Ответ: 4 см, 4 см, 4 см, 4 см.)
(Ответ: 4 см, 4 см, 4 см, 4 см.)
Задача № 318 (рис. 2).
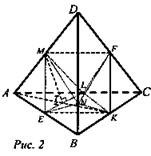
Решение: Правильный тетраэдр DABC служит каркасом (т.е. опорной фигурой) для построения правильного октаэдра. Для этого надо от каждой вершины правильного тетраэдра с ребром 2а отсечь правильный тетраэдр с ребром а. Все ребра образовавшегося внутреннего многогранника есть средние линии соответствующих граней - правильного тетраэдра, поэтому все ребра равны а, а грани многогранника - правильные треугольники со стороной равной а. По определению, полученный 8-гранник есть октаэдр. Проведем АК в пл. ABC и МT в пл. EML; Т - точка пересечения АК и EL. пл. EML || пл. BDC, значит, двугранный угол пл. BDC с плоскостью основания равен двугранному углу пл. EML с пл. ABC.
AK ⊥ EL. МT - высота в равнобедренном ΔEML, поэтому MT ⊥ EL. Отсюда ∠ATM - линейный угол двугранного угла тетраэдра (у правильного тетраэдра все двугранные углы равны). ∠MTK - линейный угол двугранного угла между плоскостями EML и KEL октаэдра. Поскольку ∠АТМ + ∠MTK = 180°, то сумма соответствующих двугранных углов тоже 180°.
III. Самостоятельная работа (см. приложение)
Решение самостоятельной работы
I-II уровни
Вариант I (рис. 3)
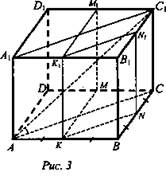
1) АС = 4√2 (см) (ΔАВС – прямоугольный), ![]()
2) ∠AC1C = 30°, так как ∠C1AC = 60°, значит, ![]()

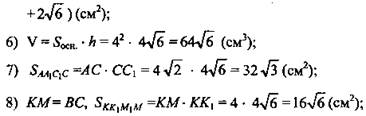
9) В ΔACB KN - средняя линия, значит, ![]()
![]()
II вариант (рис. 4).
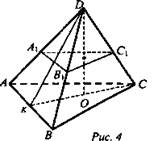
1) ![]() (из ΔСКВ);
(из ΔСКВ); ![]() (по свойству медиан)
(по свойству медиан) ![]()
![]()
2) ∠DCK - угол между DC и пл. AСB. Из ΔDOC: ![]()
![]() Варианты ответов:
Варианты ответов: ![]()
![]()
3) Из ΔDKO: ![]() ∠DKO - угол между пл. ADB и пл. ABС,
∠DKO - угол между пл. ADB и пл. ABС, ![]()
![]() Варианты ответов:
Варианты ответов: ![]()
![]()

III уровень
I вариант
№ 1 (рис. 5).
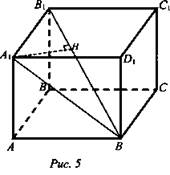
Решение:
1) ΔA1B1D - прямоугольный, А1В1 = а, тогда ![]()
![]()
2) Выразим SΔA1B1D дважды:
 (Ответ:
(Ответ: ![]() )
)
№ 2 (рис. 6)
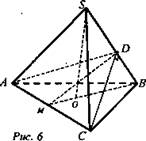
Решение:
1) Так как пл. ADC ⊥ BC, то ΔADB, ΔCDB и ΔMDB - прямоугольные; ΔADB = ΔCDB (по гипотенузе и катету, АВ = ВС = a, DB - общий катет), значит, AD = DC.
2) ВМ и DM - медианы и высоты равнобедренных треугольников, ![]()
3) О - центр окружности, описанной около основания, ![]()
4) ![]()
5) В ΔSOB и ΔMDB ∠SBM - общий ⇒ ΔSOB ~ ΔMDB (по двум углам), ![]()
6) Площадь сечения ![]() (Ответ:
(Ответ: ![]() )
)
№ 3 (рис. 7).
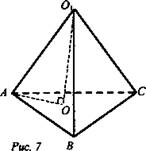
1) Так как все ребра равны, то О - центр описанной около основания окружности. AO = R.
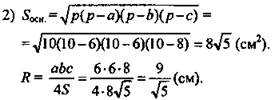
3) По теореме Пифагора: ![]()
4) ![]() (Ответ: 48 см3.)
(Ответ: 48 см3.)
Вариант I.
№ 1 (рис. 8).
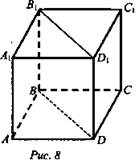
Решение:
1) Пусть АВ = х, AD = y. BD2 = х2 + у2. Площадь основания Q = ху. Из прямоугольника ![]()
2) ![]() К обеим частям прибавим удвоенное Q = ху:
К обеим частям прибавим удвоенное Q = ху: ![]()
![]()
3) Тогда, ![]() (Ответ:
(Ответ: ![]() )
)
№ 2 (рис. 9).
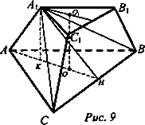
Решение:
1) OO1 - высота, О к O1- центры окружностей, описанных около оснований.
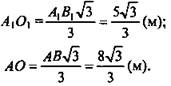
2) АН ⊥ ВС, ΔАВН: ![]()
3) ![]() по теореме о трех перпендикулярах А1Н ⊥ ВС, ∠A1HA - линейный угол искомого двугранного угла.
по теореме о трех перпендикулярах А1Н ⊥ ВС, ∠A1HA - линейный угол искомого двугранного угла.
4) А1О1ОК - прямоугольник, ![]()
![]()
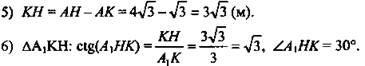
7) По теореме Пифагора ![]()
8) ![]() (Ответ: 30°, 24 м2.)
(Ответ: 30°, 24 м2.)
№ 3 (рис. 10)
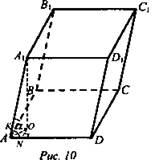
Решение:
1) Основание - прямоугольник ABCD со сторонами а и b. SABCD = ab.
2) А1O ⊥ пл. (ABC), OM ⊥ AD, ОК ⊥ АВ.
3) ΔАА1М = ΔAA1K (по гипотенузе и острому углу α). АК = AM = АА1 · cosα = с · cosα.
4) В ΔАМО и ΔАКО АО - общая сторона, ΔАМО = ΔАКО (по гипотенузе и катету), ![]()
![]()
5) ΔАА1O: ![]()
![]()
6) ![]() (Ответ:
(Ответ: ![]() )
)
IV. Подведение итогов урока
- Какие данные необходимы для нахождения объема призмы?
Домашнее задание (в трех уровнях):
1. Задачи для домашнего задания из вариантов тестов ЕГЭ.
I уровень. Боковые ребра тетраэдра попарно перпендикулярны и равны 4 м, 5 м, 6 м. Найти его объем.
II уровень. Дан правильный тетраэдр SaBC, объем которого равен V.
На ребрах SA и SB взяты их середины D и Е, а на ребре SC взята точка F такая, что SF : FC = 1 : 3. Найти объем пятигранника DEFABC.
III уровень. В правильной четырехугольной пирамиде SABCD сторона квадрата ABCD, лежащего в основании, равна √2, а высота, опущенная на основание, равна 2. Найти расстояние от точки А до плоскости SBC.
2. Повторить теорию: гл. V.
Решение домашних задач
I уровень
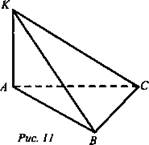
«Поставим» пирамиду на боковую грань. По условию АК ⊥ АВ, АК ⊥ АС ⇒ АК ⊥ пл. ABC, АК - высота пирамиды (рис. 11). ![]()
![]()
![]() (Ответ: 20 м3.)
(Ответ: 20 м3.)
II уровень
Решение:
1) G - середина SC, F - середина SG, EF - средняя линия ΔSBG, DF - средняя линия ΔSAG. DE - средняя линия ΔSAB (рис. 12). Тогда пирамиды SDEF и SABG подобны с коэффициентом.
2) ![]() так как SG ⊥ AG, SG ⊥ BG ⇒ SС ⊥ пл. ABG. Следовательно,
так как SG ⊥ AG, SG ⊥ BG ⇒ SС ⊥ пл. ABG. Следовательно, ![]()
![]() (Ответ:
(Ответ: ![]() )
)
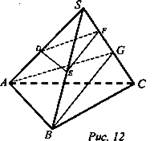
III уровень
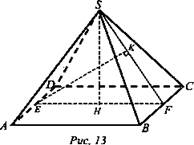
Решение: Опустим высоту SH на основание и проведем плоскость через эту высоту и точку Е, где Е - середина AD. Эта плоскость пересечет пирамиду по ΔSEF. F - середина ВС (рис. 13). В ΔSEF проведем высоту ЕК. ΔSHF ~ ΔEKF (по двум углам). ![]()
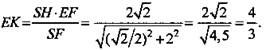 Проверим, что ЕК действительно перпендикуляр к плоскости SBC. По построению EK ⊥ SF. EF - проекция наклонной ЕК на основание пирамиды. EF ⊥ BC ⇒ по теореме о трех перпендикулярах EK ⊥ BC, так как ЕК перпендикулярна двум пересекающимся прямым, лежащим в плоскости SBC, следовательно, ЕК ⊥ пл. SBC. (Ответ: 4/3.)
Проверим, что ЕК действительно перпендикуляр к плоскости SBC. По построению EK ⊥ SF. EF - проекция наклонной ЕК на основание пирамиды. EF ⊥ BC ⇒ по теореме о трех перпендикулярах EK ⊥ BC, так как ЕК перпендикулярна двум пересекающимся прямым, лежащим в плоскости SBC, следовательно, ЕК ⊥ пл. SBC. (Ответ: 4/3.)