Поурочные разработки по Геометрии 11 класс
Повторение по теме «Объемы тел» - урок 2 - ИТОГОВОЕ ПОВТОРЕНИЕ КУРСА ГЕОМЕТРИИ 10-11 КЛАССОВ
Цели урока:
- рассмотреть задачи на комбинации тел и нахождение объемов тел вращения;
- совершенствовать навыки решения задач.
Ход урока
I. Организационный момент
Сообщить тему урока, цели урока.
II. Проверка домашнего задания
Два человека отвечают по плакатам, вывешенным на доске.
III. Актуализация знаний
1. Повторение теории (для всех случаев заготовлены чертежи на доске):
а) ГМТ, равноудаленных от двух данных (плоскость, перпендикулярная отрезку и проходящая через его середину);
б) ГМТ, равноудаленных от параллельных плоскостей (плоскость, параллельная данным и проходящая на равном расстоянии от обеих);
в) ГМТ, равноудаленных от граней двугранного угла (биссекторная плоскость);
г) ГМТ, равноудаленных от точек окружности (прямая, перпендикулярная плоскости окружности и проходящая через центр окружности);
д) ГМТ, равноудаленных от вершин многоугольника, вписанного в окружность (прямая, перпендикулярная плоскости многоугольника и проходящей через центр окружности);
е) шар вписан в многогранник (поверхность шара касается граней многогранника);
ж) шар описан около многогранника (поверхность шара проходит через все вершины многогранника);
з) шар вписан в цилиндр (конус) (поверхность шара касается оснований и всех образующих);
и) шар описан около цилиндра (конуса) (окружность оснований и вершина принадлежат поверхности шара;
к) положение центра шара, вписанного в многогранник (точка пересечения биссекторных плоскостей всех двугранных углов многогранника; всегда внутри);
л) положение центра шара, описанного около многогранника (точка пересечения плоскостей, перпендикулярных ко всем ребрам многогранника и проходящих через их середины, может лежать внутри, на поверхности, вне многогранника).
IV. Решение задач
Для каждого раздела учитель готовит плакаты с изображением взаимного расположения.
1) Шар и пирамиды
а) Если боковые грани пирамиды одинаково наклонены к основанию, то в такую пирамиду можно вписать шар. Центр шара лежит в точке пересечения высоты пирамиды с биссектрисой линейного угла любого двугранного при основании. В правильную пирамиду всегда можно вписать шар. Проекция шара на основание - круг, не вписанный в многоугольник основания, но лежащий в плоскости оси.
б) Около пирамиды можно описать шар тогда и только тогда, когда около ее основания можно описать окружность (треугольная пирамида, четырехугольная, у которой сумма противолежащих углов основания равна 180°).
Центр описанного шара лежит в точке пересечения прямой, перпендикулярной основанию и проходящей через центр окружности, описанной около основания, и плоскости, перпендикулярной любому боковому ребру и проведенной через середину этого ребра. Если боковые ребра пирамиды равны между собой (или равнонаклонны к плоскости основания), то около такой пирамиды можно описать шар. Центр шара в этом случае лежит в точке пересечения высоты пирамиды (или ее продолжения) с осью симметрии бокового ребра, лежащей в плоскости бокового ребра и высоты.
Задача № 1. В основании пирамиды лежит ромб со стороной а и острым углом α. Каждый из двугранных углов при основании равен φ. Найти объем шара, вписанного в пирамиду.
Дано: SABCD - пирамида; ABCD - ромб; АВ = а; ∠A = α. ∠((ABC); (SDС) = φ. Все боковые грани равнонаклонены к основанию (рис. 1).
Найти: Vшapa, вписанного в пирамиду.
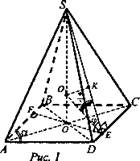
Решение: Центр вписанного шара лежит на оси пирамиды и отстоит на одно и то же расстояние, равное радиусу г шара, от всех граней пирамиды. Проведем апофему пирамиды SE, тогда r = O1O = O1К. В ромбе, лежащем в основании пирамиды, высота FE = h, и FE = asinα, ![]() тогда
тогда ![]() (Ответ:
(Ответ: ![]() )
)
Задача № 2. В шар радиуса R вписана правильная четырехугольная пирамида. Определить объем этой пирамиды, если радиус окружности, описанной около ее основания, равен r.
Дано: SABCD - правильная пирамида, вписанная в шар. R - радиус шара; r - радиус окружности описанной около ABCD.
Найти: Vпир.
Решение: CK = SK. Проведем КО1 ⊥ SC; КО1 ∩ SO = {О1} - центр описанного шара, значит O1S = О1А = O1D = О1С = R. Рассмотрим ΔO1OD - прямоугольный, по теореме Пифагора ![]()
![]()
![]() - высота пирамиды. ΔAOD - прямоугольный;
- высота пирамиды. ΔAOD - прямоугольный; ![]()
![]() (Ответ:
(Ответ: ![]() )
)
2) Шар и призма
а) В призму можно вписать шар тогда и только тогда, когда в перпендикулярное сечение этой призмы можно вписать окружность, а высота призмы равна диаметру окружности, вписанной в это перпендикулярное сечение. Если призма прямая, то проекция шара на плоскость - круг, вписанный в многоугольник основания. Например, шар можно вписать в прямую треугольную призму, если Н = 2r, в прямую четырехугольную призму у которой суммы противоположных сторон основания равны и Н = 2r, где H - высота призмы; r - радиус шара.
б) Описать шар около призмы можно тогда и только тогда, когда призма прямая и около ее основания можно описать окружность. Многоугольники основания призмы вписаны в некоторое сечение шара не проходящее через его центр; вершины призмы лежат на поверхности шара.
Задача № 3. В правильную треугольную призму вписан шар. Найти отношение объема шара к объему призмы.
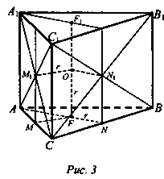
Дано: АВСА1В1С1 - правильная призма, шар вписан в призму (рис. 3).
Найти: Vш. : Vпр.
Решение:
1) Так как вписанный шар касается всех граней призмы, то его центр равноудален от всех граней призмы, а его проекцией на плоскости оснований являются центры правильных треугольников – F и F1, причем FM = FN = OF = OF1 = r.
2) ΔAMF: Пусть АВ = АС = ВС = а; тогда АМ = а/2; ∠FAM = 60°/2 = 30;
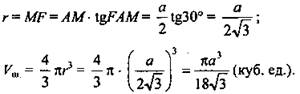
3) ![]() F1F — высота призмы;
F1F — высота призмы; ![]()
4) ![]() (Ответ:
(Ответ: ![]() .
.
3) Конус и призма
а) Прямой круговой конус можно вписать в призму, если в многоугольник основания призмы можно вписать окружность, а прямая, проходящая через центр этой окружности и перпендикулярная к плоскости основания, пересекает верхнее основание призмы (эта прямая является осью симметрии конуса). Высота конуса равна высоте призмы.
б) Прямой круговой конус описан около призмы, если все вершины верхнего основания призмы лежат на боковой поверхности конуса, а нижнее основание призмы лежит в плоскости основания конуса ⇒ около основания призмы можно описать окружность; нижнее основание призмы не вписано в основание конуса.
Задача № 4. Основанием прямой призмы служит равнобокая трапеция с острым углом а. В призму вписан конус. Найти объемы призмы и конуса, если диаметр основания конуса равен d, а угол наклона образующей конуса к плоскости его основания равен β.
Дано: ABCDA1B1C1D1 - прямая призма. ABCD - трапеция; АВ = CD; ∠A = α; конус вписан в призму; ∠SNO = β, KP = d (рис. 4).
Найти: Vк; Vпр.
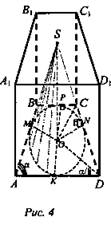
Решение:
1) ![]()
![]() - высота конуса и призмы.
- высота конуса и призмы.
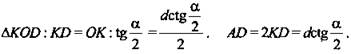
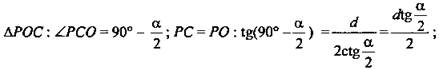
![]()
2) ![]()
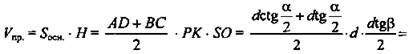
![]() (Ответ:
(Ответ: ![]() )
)
4) Пирамида и цилиндр
а) В пирамиду можно вписать прямой круговой цилиндр, причем окружность одного из оснований цилиндра касается всех боковых граней пирамиды, а другое основание цилиндра лежит в плоскости основания пирамиды, но не является вписанным в многоугольник основания; если в многоугольник основания пирамиды можно вписать окружность.
б) Пирамида считается вписанной в цилиндр, если ее основание лежит в плоскости одного из оснований цилиндра и является многоугольником, вписанным в окружность основания цилиндра, а вершина пирамиды находится в плоскости другого основания цилиндра.
Задача № 5. В правильную четырехугольную пирамиду с плоским углом α при вершине вписан цилиндр.
Найти объемы тел, если высота цилиндра в два раза меньше высоты пирамиды, а радиус его основания равен r.
Дано: SABCD - правильная пирамида, цилиндр вписан в пирамиду. SO = 2OO1, ON = O1N1 = r (рис. 5).
Найти: Vпир., Vцил.
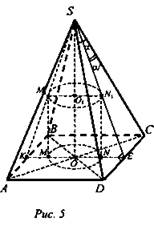
Решение:
1) Центры оснований пирамиды и цилиндра совпадают - точка О. ΔSON1 ~ ΔSOE (по 2-м углам) ⇒ ![]()
![]()
2) ΔDSC: так как пирамида правильная, то SD = SC, тогда SE - медиана и биссектриса ⇒ ![]()
![]()
3) ![]()
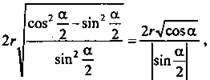 но α - плоский угол в правильной четырехугольной пирамиде, значит
но α - плоский угол в правильной четырехугольной пирамиде, значит ![]() - острый ⇒
- острый ⇒ ![]() Таким образом,
Таким образом, 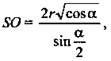 тогда
тогда 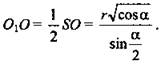
4) 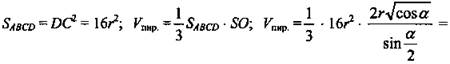
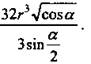
5) 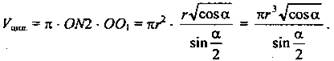 (Ответ:
(Ответ: 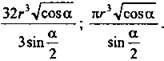 )
)
5) Конус и шар
а) В шар можно вписать конус. При этом вершина конуса и все точки его основания лежат на поверхности шара, а центр шара лежит на высоте конуса.
б) Шар можно вписать в конус, при этом каждая образующая конуса является касательной к поверхности шара и плоскость основания конуса касается поверхности шара.
Если провести осевое сечение конуса, то в сечении получим равнобедренный треугольник, в который вписано диаметральное сечение шара.
в) Шар можно вписать в усеченный конус тогда и только тогда, когда осевым сечением конуса служит равнобокая трапеция, в которую можно вписать окружность.
Задача № 6. Определить объем усеченного конуса с образующей, равной l, описанного около шара радиуса r.
Дано: шар вписан в усеченный конус. CD = l; OO2 = OO1 = ОК = r (рис. 6).
Найти: Vу.к.
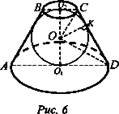
Решение:
1) Рассмотрим осевое сечение конуса - равнобокую трапецию ABCD. Окружность (О; r) вписана в ABCD, значит АВ + CD = ВС + AD.
Пусть O2С = R2; O1D = R2, тогда 2R1 + 2R2 = 21 ⇒ R1 + R2 = l.
2) ∠O2CD + ∠O1DC = 180°, но ОС и OD - биссектрисы этих углов, значит ∠DCO + ∠CDO = 180°/2 = 90° ⇒ ∠COD = 90°, т. е. ΔCOD - прямоугольный. ОК - высота, опущенная на гипотенузу, поэтому OK2 = СК · KD. По свойству касательных, проведенных к окружности из одной точки СК = СO2 = R2; KD = O1D = R1 и значит, OK2 = R1 · R2, т. е. R1 · R2 = r2.
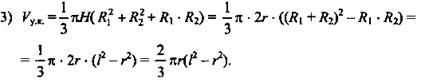
(Ответ: ![]() )
)
V. Подведение итогов
Вопросы:
- Какие вопросы теории повторили на этом уроке?
- По каким формулам вычисляют объем шара, пирамиды, призмы, конуса, усеченного конуса, цилиндра?
Выставление оценок. В журнал выставляются оценки за домашнюю работу только учащимся, получившим неудовлетворительные оценки за работу на уроке.
Домашнее задание
Указания к домашнему заданию (все готовят решения на двойных листах и сдают к следующему уроку).
Дома:
№ 1. В правильной треугольной пирамиде высота равна 3, а объем равен 9√3 . Найти радиус сферы, описанной около пирамиды.
Дано: правильная треугольная пирамида SABC; SO = 3; V = 9√3 (куб. ед.) (рис. 7).
Сфера описана около пирамиды.
Найти: O1S = O1С = R.
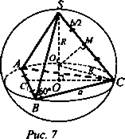
Решение: Пусть АВ = ВС = а, тогда так как ![]() получим
получим ![]() О - центр основания призмы ⇒
О - центр основания призмы ⇒ ![]() Точка О1 лежит на пересечении прямой SO и серединного перпендикуляра МО1 к ребру SC, проведенному в плоскости SOC. Пусть SC = b, тогда
Точка О1 лежит на пересечении прямой SO и серединного перпендикуляра МО1 к ребру SC, проведенному в плоскости SOC. Пусть SC = b, тогда ![]() ΔSOC ~ ΔSMO1 (no 2-м углам) ⇒
ΔSOC ~ ΔSMO1 (no 2-м углам) ⇒ 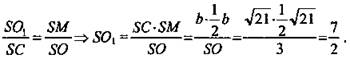 (Ответ: 3,5.)
(Ответ: 3,5.)
№ 2. Найти отношение объема шара к объему описанного около него конуса с равносторонним осевым сечением.
Дано: Шар вписан в конус. ΔАВС - осевое сечение АВ = ВС = АС (рис. 8).
Найти: Vш.: Vк.
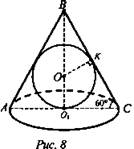
Решение:
1) Окружность диаметрального сечения шара вписана в равносторонний треугольник ABC. Пусть АВ = ВС = АС = а, тогда ![]() и
и ![]()
2) ΔАВС: ВО1 - высота, биссектриса, медиана, поэтому ![]()
![]()
![]()
3) ![]() Интересно, что и отношение площадей поверхности такого конуса и шара равно 4 : 9. (Ответ: Vш.: Vк. = 4 : 9.)
Интересно, что и отношение площадей поверхности такого конуса и шара равно 4 : 9. (Ответ: Vш.: Vк. = 4 : 9.)