Уроки-конспекты по Геометрии 8 класс
ПРИЗНАКИ ПОДОБИЯ ТРЕУГОЛЬНИКОВ - урок 4
Цели: доказать третий признак подобия треугольников, рассмотреть решение задач с применением изученных признаков подобия.
Ход урока
I. Проверка домашнего задания.
Выполнить устно:
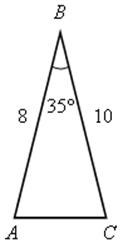
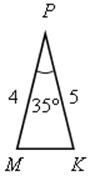
1. Подобны ли треугольники АВС и МРK?
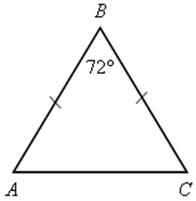
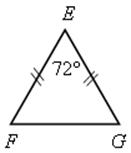
2. Подобны ли треугольники АВС и FEG?
3. Найти подобные треугольники.
Ответ: АВС ![]() ВDС.
ВDС.
4. Можно ли утверждать:
1) что все равнобедренные треугольники подобны?
2) все прямоугольные равнобедренные треугольники подобны?
3) все равносторонние треугольники подобны?
II. Изучение нового материала.
Доказательство третьего признака подобия треугольников.
III. Закрепление изученного материала.
Выполнить задание (устно).
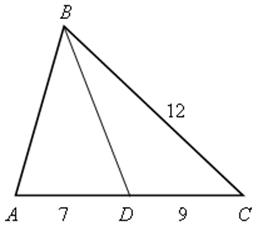
1. Найти подобные треугольники:
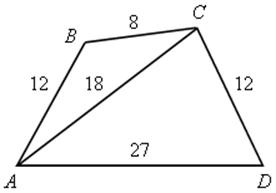
Решение
Рассмотрим ![]() АВС и
АВС и ![]() АСD.
АСD.
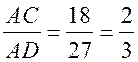 .
.
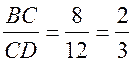 .
.
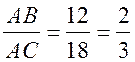 .
.
![]() АВС
АВС ![]()
![]() АСD.
АСD.
2. В треугольнике АВС АВ = 4, ВС = 6, АС = 9. Точка Е лежит на стороне ВС. Внутри треугольника взята точка М так, что МВ = 1![]() , МЕ = 2
, МЕ = 2![]() , СЕ = 2. Докажите, что МЕ || АС.
, СЕ = 2. Докажите, что МЕ || АС.
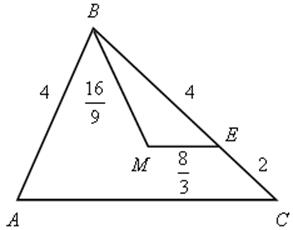
Решение
1) Рассмотрим ![]() АВС и
АВС и ![]() ВМЕ.
ВМЕ.
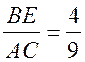 ;
; 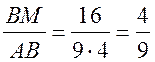 .
.
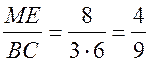 .
.
По третьему признаку подобия треугольников![]() АВС
АВС ![]()
![]() ВМЕ.
ВМЕ.
2) ![]() ВЕМ =
ВЕМ =![]() ВСА как углы подобных треугольников.
ВСА как углы подобных треугольников.
3) МЕ || АС, так как соответственные углы ![]() ВЕМ =
ВЕМ =![]() ВСА при секущей ВС.
ВСА при секущей ВС.
3. В треугольнике АВС АВ = 4, ВС = 6, АС = 7. Точка Е лежит на стороне АВ. Внутри треугольника взята точка М так, что МВ = 5![]() , МЕ = 4
, МЕ = 4![]() , АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что
, АЕ = 1. Прямая ВМ пересекает АС в точке Р. Докажите, что ![]() АРВ равнобедренный.
АРВ равнобедренный.
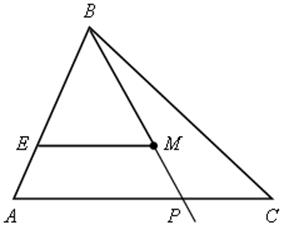
Решение
1) Рассмотрим ![]() ВАС и
ВАС и ![]() ЕВМ.
ЕВМ.
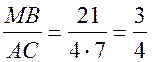 .
.
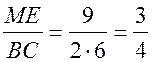 .
.
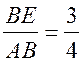 .
.
2) ![]() ВАС
ВАС ![]()
![]() ЕВМ по третьему признаку подобия треугольников.
ЕВМ по третьему признаку подобия треугольников.
3) ![]() ЕВМ =
ЕВМ = ![]() ВАС как соответственные углы подобных треугольников.
ВАС как соответственные углы подобных треугольников.
4) ![]() АВР равнобедренный.
АВР равнобедренный.
IV. Итоги урока.
Домашнее задание: вопросы 1–6, с. 160; №№ 560 (а), 613.
Для желающих.
Сторона СD параллелограмма АВСD продолжена за точку D на отрезок DF, равный стороне СD, и точка F соединена отрезком с серединой Е стороны АВ. Доказать, что отрезок FЕ отсекает от диагонали АС пятую часть, а от стороны АD – третью часть.
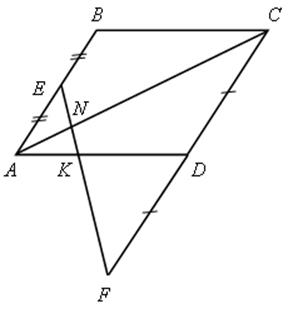
Решение
1) AE = ![]() AB, AE =
AB, AE = ![]() FC.
FC.
2) ![]() АЕN
АЕN ![]()
![]() CFN.
CFN.
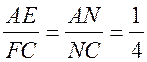 , то есть AN – пятая часть диагонали АС.
, то есть AN – пятая часть диагонали АС.
3) ![]() АЕK
АЕK ![]()
![]() DFK.
DFK.
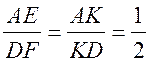 , то есть АK – третья часть стороны АD.
, то есть АK – третья часть стороны АD.