СООТНОШЕНИЯ МЕЖДУ СТОРОНАМИ И УГЛАМИ ПРЯМОУГОЛЬНОГО ТРЕУГОЛЬНИКА - урок 2

Цель: найти значения синуса, косинуса и тангенса для углов 30°, 45°, 60° и других углов.

Ход урока

I. Проверка домашнего задания.

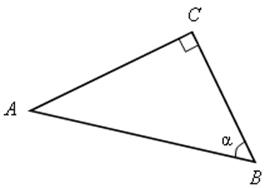
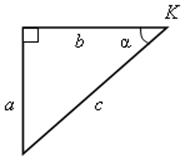
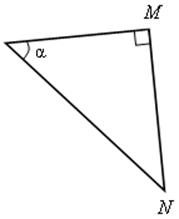
Записать sin α, cos α, tg α для данных треугольников.

2. Катеты треугольника равны 3 см и 4 см. Чему равны синусы его острых углов.

3. Гипотенуза АВ прямоугольного треугольника равна 10 см, а катет ВС равен 8 см. Чему равны тангенсы его острых углов?

II. Объяснение нового материала.

1. Выполнить устно:

АВСD – параллелограмм.

Найти: SABCD.

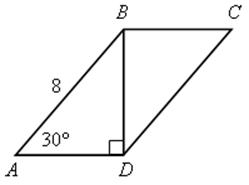
АВСD – прямоугольная трапеция.

Найти: SABCD.

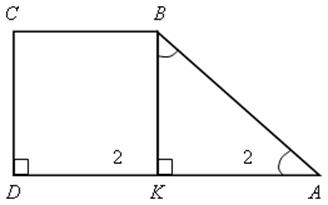
Найти: ВK.

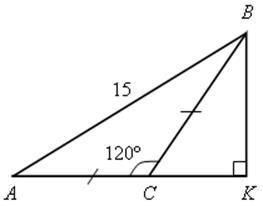
2. Вычислить значения синуса, косинуса и тангенса для углов 30°, 45° и 60° и занести их в таблицу.

3. Показать, как пользоваться микрокалькулятором для вычисления значений других углов.

III. Закрепление изученного материала.

№ 593 (а) – для значения α = 30°, № 593 (б) – для значений α = 45° (устно), №№ 601, 594, 597 (б), 598 (а).

№ 594.

Дано: а) АВС, С = 90°, АС = b, В = β.

Найти: ВС, АВ, А.

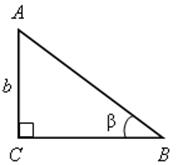
Решение

1. .

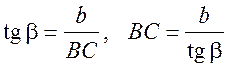2. AB = .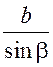

3. А = 90° – β.

Дано: б) АВС, С = 90°, b = 10 cм, β = 50°.

Найти: ВС, АВ, А.

Решение

1. BC = 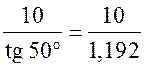≈ 8,39 (см).

2. AB = 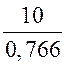≈ 13,05 (см).

3) А = 90° – β.

№ 597 (б).

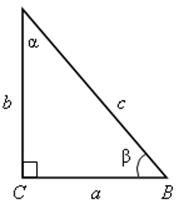
Решение

1) (см).

tg β = 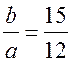= 1,25; β ≈ 51°21′,

tg α = 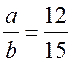= 1,25; α ≈ 38°39′ или α = 90° – 51°21′ = 89°60′ – 51°21′ = 38°39′.

№ 598.

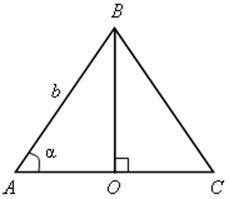
Решение

1) sin α = ; BO = AB sin α = b sin α.

2) cos α = ; AO = AB cos α = b cos α.

3) SАВС = BO ∙ AC = BO ∙ AO.

4) SАВС = b sin α · b cos α = b2sin α cos α.

IV. Итоги урока.

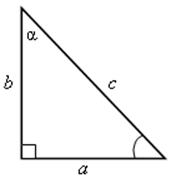
Для вычисления неизвестных элементов (сторон или углов) прямоугольного треугольника используют определения синуса, косинуса и тангенса острого угла:

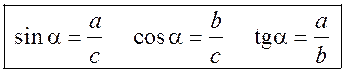
Здесь: а – катет, противолежащий углу α;

b – катет, прилежащий к углу α;

с – гипотенуза.

При решении задач необходимо: выбрать нужную формулу, подставить в нее известные величины, вычислить неизвестную величину, решив полученное уравнение.

Домашнее задание: вопрос 18, с. 161; №№ 595, 596, 598 (б), 600; подготовиться к самостоятельной работе по § 3.