Уроки-конспекты по Геометрии 8 класс
ЦЕНТРАЛЬНЫЕ И ВПИСАННЫЕ УГЛЫ - урок 4
Цели: учить применять полученные знания при решении задач; способствовать развитию навыка решения задач.
Ход урока
I. Проверка домашнего задания.
№ 667 рассмотреть решение на доске.
II. Решение задач (устно).
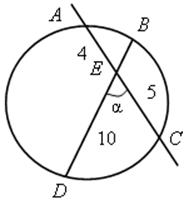
1)Найти: ВЕ и α.
После решения задачи обратить внимание: угол, вершина которого лежит внутри круга, измеряется полусуммой двух дуг, одна из которых заключена между его сторонами, а другая – между продолжениями сторон.
α = ![]() (
(![]() AB +
AB + ![]() CD).
CD).
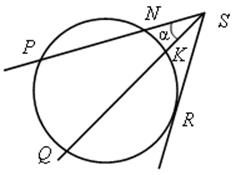
2) SN = 4; SP = 9; SK = 3.
Найти: SR, SQ, α.
После решения задачи обратить внимание: угол, вершина которого лежит вне круга, измеряется полуразностью двух дуг, заключенных между его сторонами.
α = ![]() (
(![]() PQ –
PQ – ![]() NK).
NK).
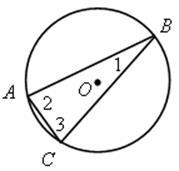
3) ![]() АС :
АС : ![]() АВ :
АВ : ![]() СВ = 3 : 7 : 8.
СВ = 3 : 7 : 8.
Найти: ![]() 1,
1, ![]() 2,
2, ![]() 3.
3.
4) Окружность проходит через вершины В, С, D трапеции АВСD (АD и ВС – основания) и касается стороны АВ в точке В.
Докажите, что ВD = ![]() .
.
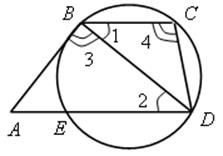
Решение
1) Так как ВС || АD, то ![]() 1 =
1 = ![]() 2.
2.
2) ![]() 3 =
3 = ![]()
![]() BED,
BED, ![]() 4 =
4 = ![]()
![]() BED,
BED, ![]() 3 =
3 = ![]() 4.
4.
3) ![]() АВD
АВD ![]()
![]() ВСD (по двум углам).
ВСD (по двум углам).
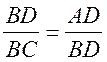 ; BD2 = BC ∙ AD; ВD =
; BD2 = BC ∙ AD; ВD = ![]() .
.
III. Самостоятельная работа.
Вариант I
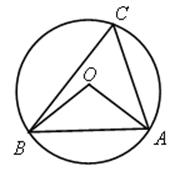
1. Точки А, В, С лежат на окружности с центром О, ![]() АОВ = 80°,
АОВ = 80°, ![]() АС :
АС : ![]() ВС = 2 : 3.
ВС = 2 : 3.
Найдите углы треугольника АВС.
2. Хорды АВ и СD пересекаются в точке K, причем хорда АВ делится точкой К на отрезки, равные 10 см и 6 см. На какие отрезки точка K делит хорду СD, если СD > АВ на 3 см?
Вариант II
1. Вершины треугольника АВС лежат на окружности с центром О (см. рис. к задаче 1 I варианта), ![]() АВС = 80°,
АВС = 80°, ![]() ВС :
ВС : ![]() АВ = 3 : 2. Найдите углы треугольника АОВ.
АВ = 3 : 2. Найдите углы треугольника АОВ.
2. Хорды MN и KL пересекаются в точке А, причем хорда MN делится точкой А на отрезки, равные 1 см и 15 см. На какие отрезки точка А делит хорду KL, если KL в два раза меньше MN?
Вариант III
(для более подготовленных учащихся)
1. Окружность с центром О касается сторон АВ, ВС, АС треугольника АВС соответственно в точках K, M, N, ![]() KМ :
KМ : ![]() MN :
MN : ![]() NK = 6 : 5 : 7. Найдите углы треугольника АВС.
NK = 6 : 5 : 7. Найдите углы треугольника АВС.
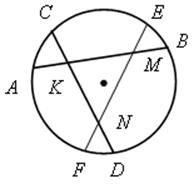
2. Хорды АВ, СD, EF окружности с центром О попарно пересекаются в точках K, М, N, причем каждая хорда делится этими точками на равные части. Найдите периметр треугольника KMN, если АВ = 12 см.
IV. Итоги урока.
Домашнее задание: вопросы 1–14, с. 187; №№ 665, 669.
№ 669.
Решение
Дано: ![]()
Построить: отрезок ХY = ![]() .
.
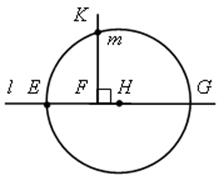
Построение.
1) Отложим на произвольной прямой l отрезки EF = АВ и FG = СD.
2) Разделим отрезок EG пополам и получим точку H.
3) Проведем окружность с центром в точке Н и радиусом ЕН.
4) Из точки F восстановим перпендикуляр m к прямой l и пусть K – любая из точек пересечения m с окружностью.
5) FK – искомый отрезок.
Для желающих.
Через точку пересечения окружности с биссектрисой описанного угла проведена хорда, параллельная одной стороне угла. Докажите, что эта хорда равна другой стороне вписанного угла.
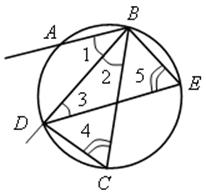
Решение
1) Так как DЕ || АВ и ВD – биссектриса угла АВС, то ![]() 1 =
1 = ![]() 2 =
2 = ![]() 3.
3.
2) ![]() 4 =
4 = ![]() 5 как вписанные, опирающиеся на одну дугу ВD.
5 как вписанные, опирающиеся на одну дугу ВD.
3) ΔВСD = ΔDЕВ (по стороне и двум углам).
4) DЕ = ВС.