ВПИСАННАЯ И ОПИСАННАЯ ОКРУЖНОСТИ

Цели: ввести понятие вписанной окружности и описанного около окружности многоугольника; рассмотреть теорему о том, что в любой треугольник можно вписать окружность.

Ход урока

I. Проверка домашнего задания.

Выполнить устно:

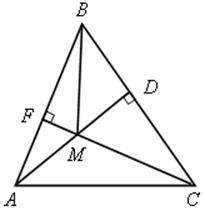
1) а) Докажите, что АВМ = МСА.

б) АМ = 4, МD = 3, ВD = 4.

Найдите расстояние от точки М до стороны АС.

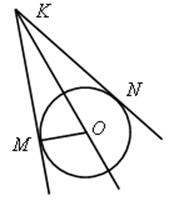
2) Найдите МKN и расстояние MN, если ОМ = , KМ = 3.

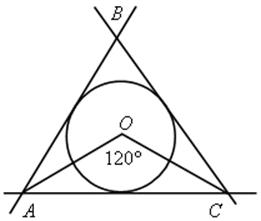
3) Найдите углы АВС, если ОАС = 20° и АОС = 120°.

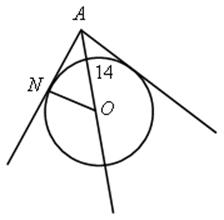
4) стороны угла А касаются окружности радиуса r с центром О.

а) Найдите ОА, если r = 5 см, А = 60°.

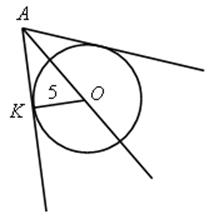
б) Найдите r, если ОА = 14 дм, А = 90°.

II. Изучение нового материала.

Изложить в виде лекции п. 74 до замечания 2.

III. Закрепление изученного материала.

Выполнить №№ 701 (для остроугольного треугольника), 689, 691.

№ 689.

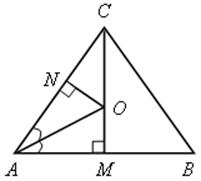
Решение

1) Центр О вписанной окружности искомого радиуса r лежит на биссектрисе СМ треугольника АВС, а так как СМ АВ, то вписанная окружность касается отрезка АВ в точке М. Поэтому ОМ = r.

Далее обсудить с учащимися различные способы решения этой задачи:

I способ.

1. АМ = AB = 5 см.

2. M и N – точки касания, следовательно, AN = АМ = 5 см, откуда CN = АС – АN = 8 cм.

3. В АСМ : СМ = = 12 (см).

4. В СON : СО2 = СN2 + ON2, то есть (12 – r)2 = 82 + r2

144 – 24r + r2 = 64 + r2.

r = 3.

ОМ = ON = 3 см.

II способ.

1. В АСМ : АМ = AB = 5 см.

СМ = = 12 (см).

2. Отрезок АО – биссектриса треугольника АМС (так как О – центр вписанной окружности), поэтому 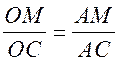или 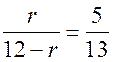; 13r = 60 – 5r, r = 3.

ОМ = ОN = 3 см.

IV. Итоги урока.

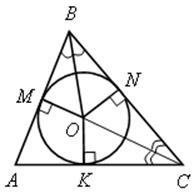
1) Центр вписанной в треугольник окружности в точке пересечения биссектрис;

2) ОМ = ON = ОK – радиусы вписанной окружности;

3) окружность единственная для данного треугольника.

Домашнее задание: вопросы 21, 22, с. 188; №№ 701 (для прямоугольного и тупоугольного треугольников), 637, 690, 693 (а), 693 (б) – по желанию и используя № 697 III способ решения № 698.

№ 690.

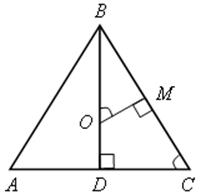
Решение

1) О – центр вписанной окружности в треугольник АВС, который лежит на высоте (биссектрисе) равнобедренного треугольника, проведенной к основанию.

2) ОМ = ОD – радиусы этой окружности.

3) Пусть k – коэффициент пропорциональности, тогда ОВ = 12k см, ОD = ОМ = 5k см.

4) Прямоугольные треугольники ВDС и ВМО имеют общий угол В, и, значит, ВDС ВМО по первому признаку.

5) .

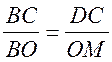6) Из прямоугольного треугольника ВDС по теореме Пифагора имеем:DС = .

7) 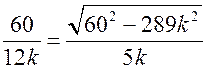; 5 = ;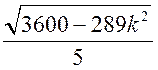

625 = 3600 – 289k2

k2 = .

8) DC = 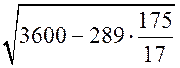= 25 (cм).

№ 693 (а).

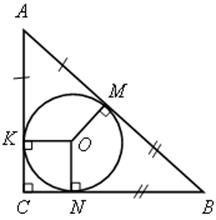
Решение

1) АС || ОN, так как АС СВ и ON CВ.

СВ || ОK, так как СВ АС и OK АС, значит, четырехугольник KONC – прямоугольник, а так как KО = CN = r = ON = KC, то KONC – квадрат.

2) АKО = АМО (по катету и гипотенузе), поэтому АK = АМ.

3) ВNO = ВМО (по катету и гипотенузе).

4) РАВС = АВ + ВС + АС = АМ + МВ + NB + CN + KC + АK.

РАВС = 2АМ + 2MВ + 2CN = 2(АМ + МВ + СN).

а) РАВС = 2(АВ + СN) = 2(26 + 4) = 60 (см).

б) Из АВС, С = 90° имеем по теореме Пифагора:

АС2 = АВ2 – СВ2 = АВ2 – (CN + NB) = 172 – (5 + r)2

ВС2 = АВ2 – АС2 = АВ2 – (АK + KС) = 172 – (12 + r)2

АВ2 = АС2 + ВС2

172 = 172 – (5 + r)2 + 172 – (12 + r)2

2r2 + 34r – 120 = 0

r2 + 17r – 60 = 0

r = 3 (второй корень не удовлетворяет условию задачи).

РАВС = 2(АВ + CN) = 2(17 + 3) = 40 (см).