ПАРАЛЛЕЛОГРАММ И ТРАПЕЦИЯ - урок 6

Цели: продолжить знакомить учащихся с задачами на построение. Научить делить отрезок на n равных частей.

Ход урока

I. Проверка домашнего задания.

Трое учащихся на доске готовят решение домашних задач.

№ 392 (а).

АN = 7 – 4 = 3 (cм)

АВ = 2АN = 6 (cм)

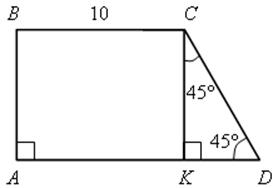
392 (б).

KD = АD – АK = 15 – 10 = 5 (см)

KD = KС = 5 (см)

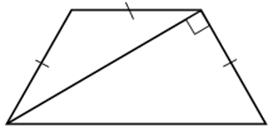
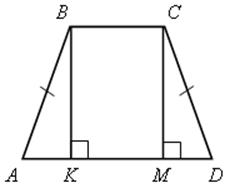
1) АD = АK + МD + ВС, так как АK = МD

АD – ВС = 2МD

МD = (АD – ВС)

2) АD + ВС = АМ + МD + ВС

АD + ВС = АМ + KD, так как АМ = KD

АD + ВС = 2АМ

АМ = (АD + ВС).

В это время остальные решают устно задачу:

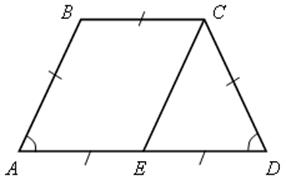
Меньшее основание равнобокой трапеции равно боковой стороне и в 2 раза меньше другого основания.

Найти углы трапеции.

Решение

АЕ = ЕD, проведем СЕ.

1) АВСЕ – параллелограмм, так как ВС || АЕ и ВС = АЕ. Имеем АВ = СЕ = ЕD = СD.

2) СЕD равносторонний D = 60°.

3) А = 60°, В = С = 180° – 60° = 120°.

II. Решение задач.

Напомнить основные этапы решения задач на построение:

1) Анализ задачи.

2) Выполнение построения по намеченному плану.

3) Доказательство того, что построенная фигура удовлетворяет условиям задачи.

4) Исследование задачи.

№ 393 (в) (решение в учебнике).

№ 394. Пусть А, В, С – данные точки.

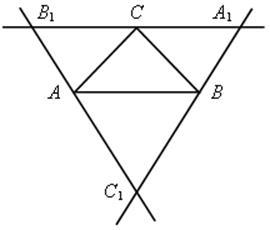
Соединим попарно эти точки и через каждую вершину треугольника АВС проведем прямую, параллельную противолежащей стороне.

Четырехугольники В1ВАС, С1АСВ, В1АВС – параллелограммы по определению.

Задача имеет только эти три решения, так как не существует других прямых, проходящих через точки А, В, С и параллельных прямых ВС, АС, АВ соответственно.

№ 395.

Дано:

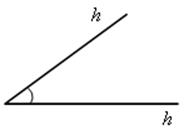
Построить АВСD – параллелограмм.

Построение

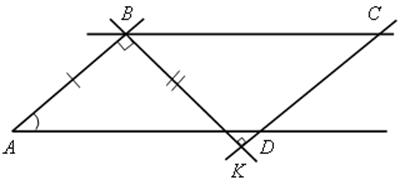
А = kh, АВ = Р1Q1

P2Q – расстояние между АВ и СD.

Устно провести анализ, доказательство и исследование, в тетрадях – только построение:

1) построить А, равный данному hk;

2) отложить на его стороне отрезок Р1Q = АВ и отметить точку В;

3) через точку В провести прямую, перпендикулярную прямой АВ и отложить отрезок ВK = Р2Q2;

4) через точку В провести прямую, параллельную другой стороне угла;

5) через точку K провести прямую, параллельную стороне АВ;

6) АВСD – параллелограмм по определению.

№ 397 (а).

Дано:

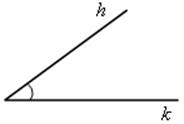
Построить трапецию АВСD: АD || ВС, АВ = СD, АD = MN, АВ = М1N1, А = hk.

Построение

1) Строим АВD так, чтобы АD = МN, АВ = М1N1, А = hk.

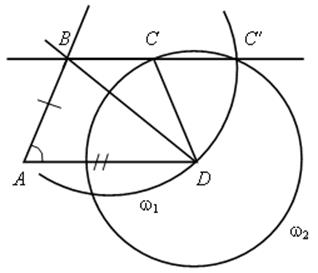
2) Через точку В проведем прямую, параллельную прямой АD. Для этого проведем две окружности: окружность ω1 с центром В радиуса ВD и окружность ω2 с центром D радиуса АВ. Пусть С′ – точка пересечения этих окружностей, лежащая по ту сторону от прямой АD, что и точка В. Тогда ВС′ || АD.

3) Окружность ω2 пересекает прямую ВС еще в одной точке – точке С. Соединив эту точку с точкой D, получаем искомую трапецию АВСD. Если hk = 90°, то задача не имеет решения.

III. Итоги урока.

Домашнее задание: №№ 393 (в), 396, 398, 397 (б); повторить свойства и признаки параллелограмма.

Найти углы трапеции.