Информатика - Методическое пособие для 7-9 классов - 2015 год
Алгоритмы и исполнители - МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ПРОВЕДЕНИЮ УРОКОВ В 8 КЛАССЕ
Планируемые образовательные результаты:
• предметные — понимание смысла понятия “алгоритм”; умение анализировать предлагаемые последовательности команд на предмет наличия у них таких свойств алгоритма, как дискретность, определенность, понятность, результативность, массовость; понимание терминов “исполнитель”, “формальный исполнитель”, “среда исполнителя”, “система команд исполнителя” и др.; умение исполнять алгоритм для формального исполнителя с заданной системой команд;
• метапредметные — понимание смысла понятия “алгоритм” и широты сферы его применения; понимание ограничений, накладываемых средой исполнителя и системой команд на круг задач, решаемых исполнителем;
• личностные — алгоритмическое мышление, необходимое для профессиональной деятельности в современном обществе.
Решаемые учебные задачи:
1) обобщение первоначальных представлений учащихся о понятиях “алгоритм” и “исполнитель”;
2) рассмотрение свойств алгоритма;
3) рассмотрение возможности автоматизации деятельности человека за счет возможности формального исполнения алгоритма.
Основные понятия, рассматриваемые на уроке:
• алгоритм;
• свойства алгоритма:
- дискретность;
- понятность;
- определенность;
- результативность;
- массовость;
• исполнитель;
• характеристики исполнителя:
- круг решаемых задач;
- среда;
- режим работы;
- система команд;
• формальное исполнение алгоритма.
Средства ИКТ, используемые на уроке:
• персональный компьютер (ПК) учителя, мультимедийный проектор, экран;
• ПК учащихся.
Электронное приложение к учебнику:
• презентация “Алгоритмы и исполнители”.
Единая коллекция цифровых образовательных ресурсов:
• лекция по теме “Наибольший общий делитель” (185111);
• лекция по теме “Наименьшее общее кратное” (184642);
• анимация “Решето Эратосфена” (180279);
• демонстрация к лекции “Исполнитель алгоритма” (128639);
• демонстрация к лекции “Происхождение и определение понятия алгоритма” (126137);
• демонстрация к лекции “Свойства алгоритма” (128655).
Особенности изложения содержания темы урока
Изложение нового материала ведется на основании презентации “Алгоритмы и исполнители” с привлечением дополнительных анимаций и демонстраций.
В ходе урока по выбору учителя решаются различные задачи из параграфа и из рабочей тетради.
Домашнее задание
§ 2.1; вопросы и задания № 1-20 к параграфу; № 102, 108 в РТ.
Дополнительные задания: № 104, 110 в РТ.
Указания, комментарии, ответы и решения
Задания в учебнике
№ 14. 1, 1, 2, 3, 5, 8, 13, 21, 34, 55. Последовательность Фибоначчи.
№ 15. См. комментарии к № 106 в РТ.
№ 16. Один из вариантов: Например, сайт http://ru.wikipedia.org/wiki/Решето_Эратосфена.
№ 17. Правильный восьмиугольник. Для исполнителя Черепаха (КуМир) соответствующая программа и результат работы будут выглядеть так:

№ 18. а) 12211; б) 22211.
№ 19. Если к числу 8 применить алгоритм 22212, то получится число 6.
Алгоритм 12212 преобразует число 1 в число 16.
№ 20. В клетке В.
Задания в рабочей тетради
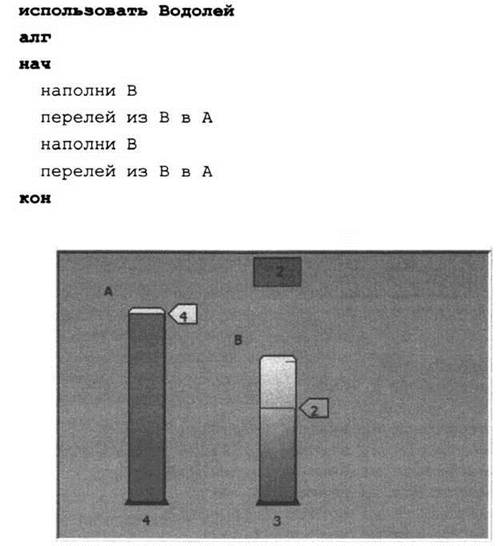
№ 96. Возможный вариант: 2424. Для исполнителя Водолей (КуМир) соответствующая программа и результат работы будут выглядеть так:
№ 97
|
Исходные данные |
1-я кучка |
2-я кучка |
1-я кучка |
2-я кучка |
|
30 |
51 |
52 |
12 |
|
|
1-й шаг |
30 |
21 |
40 |
12 |
|
2-й шаг |
9 |
21 |
28 |
12 |
|
3-й шаг |
9 |
12 |
16 |
12 |
|
4-й шаг |
9 |
3 |
4 |
12 |
|
5-й шаг |
6 |
3 |
4 |
8 |
|
6-й шаг |
3 |
3 |
4 |
4 |
Ответ: 6 шагов.
№ 98. Можно работать с исполнителем Чертежник в среде КуМир.
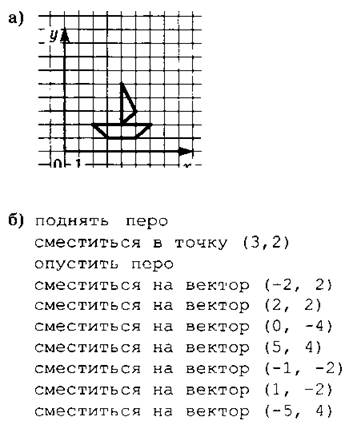
№ 99


№ 100
а) 132; 142.
б) 142; 132.
в) Более короткого алгоритма, гарантирующего тот же результат, нет; 4113232.
№ 101. Назад 5.
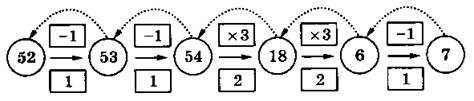
№ 102. В п. а) схема уже частично заполнена, кроме того, приведена и программа получения из числа 2 числа 13. Это сделано для того, чтобы ученикам стали более понятны правила заполнения схемы,
а) 21211
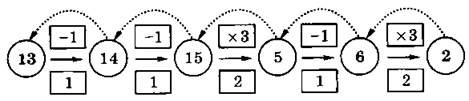
б) 11221
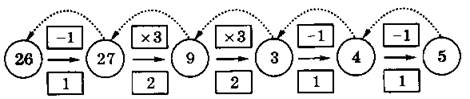
в) 12211
№ 103
а) 8 алгоритмов.
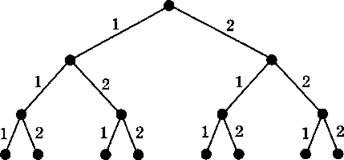
б)
|
111 |
8 |
|
112 |
18 |
|
121 |
14 |
|
122 |
36 |
|
211 |
10 |
|
212 |
24 |
|
221 |
20 |
|
222 |
54 |
в) 2112.
г) 121121.
№ 104. 104 = 11010002.
1-й шаг: 011010000
2-й шаг: 110100000
3-й шаг: 10011111
4-й шаг: 10011110
5-й шаг: 100111100
1111002 = 60.
Ответ: 60.
№ 105. Решаем методом исключения, проверяя для каждого случая соблюдение правил формирования цепочки: первому правилу (правилу для первой бусины) удовлетворяют все цепочки; второму правилу (правилу для второй бусины) не удовлетворяет цепочка 2; третьему правилу (правилу для третьей бусины) не удовлетворяют цепочки 1 и 3. Всем правилам соответствует цепочка 4.
№ 106
|
Исходная цепочка |
КОМ |
шок |
|
1-й шаг |
коммок |
шоккош |
|
2-й шаг |
коммокн |
шоккошл |
|
3-й шаг |
коммокннкоммок |
шоккошллшоккош |
|
4-й шаг |
коммокннкоммоко |
шоккошллшоккошщ |
|
Результат |
коммокннкоммоко |
шоккошллшоккошщ |
|
Количество букв “О” в результате |
5 |
4 |
№ 107
|
Исходная цепочка |
МАК |
НИЛ |
КОШ |
|
1-й шаг: записать в начало новой цепочки букву, следующую по алфавиту за первой буквой исходной цепочки |
Н |
О |
Л |
|
2-й шаг: дописать после первой буквы результата две последние буквы исходной цепочки в обратном порядке |
НКА |
ОЛИ |
ЛШО |
|
3-й шаг: дописать первую букву исходной цепочки |
НКАМ |
ОЛИН |
ЛШОК |
|
Результат |
НКАМ |
ОЛИН |
ЛШОК |
№ 108
|
Номер строки |
Строка |
|
1 |
0 |
|
2 |
10 |
|
3 |
201 |
|
4 |
3102 |
|
5 |
42013 |
|
6 |
531024 |
|
7 |
6420135 |
|
8 |
75310246 |
|
9 |
864201357 |
|
10 |
9753102468 |
Ответ: 2468.
№ 109. 2 (1 048 576).
№ 110. Возможный вариант:
|
№ дня |
Бригада 1 |
Бригада 2 |
Бригада 3 |
|
1 |
установи (5) |
установи (4) |
установи (3) |
|
2 |
установи (2) |
установи (8) |
установи (9) |
|
3 |
установи (7) |
установи (13) |
установи (12) |
|
4 |
установи (1) |
установи (11) |
установи (15) |
|
5 |
установи (б) |
установи (14) |
установи (17) |
|
6 |
установи (10) |
установи (16) |
установи (18) |